基础知识:
动态规划背包问题-CSDN博客
动态规划基础概念-CSDN博客
题目练习:
题目1:过河卒
题目描述
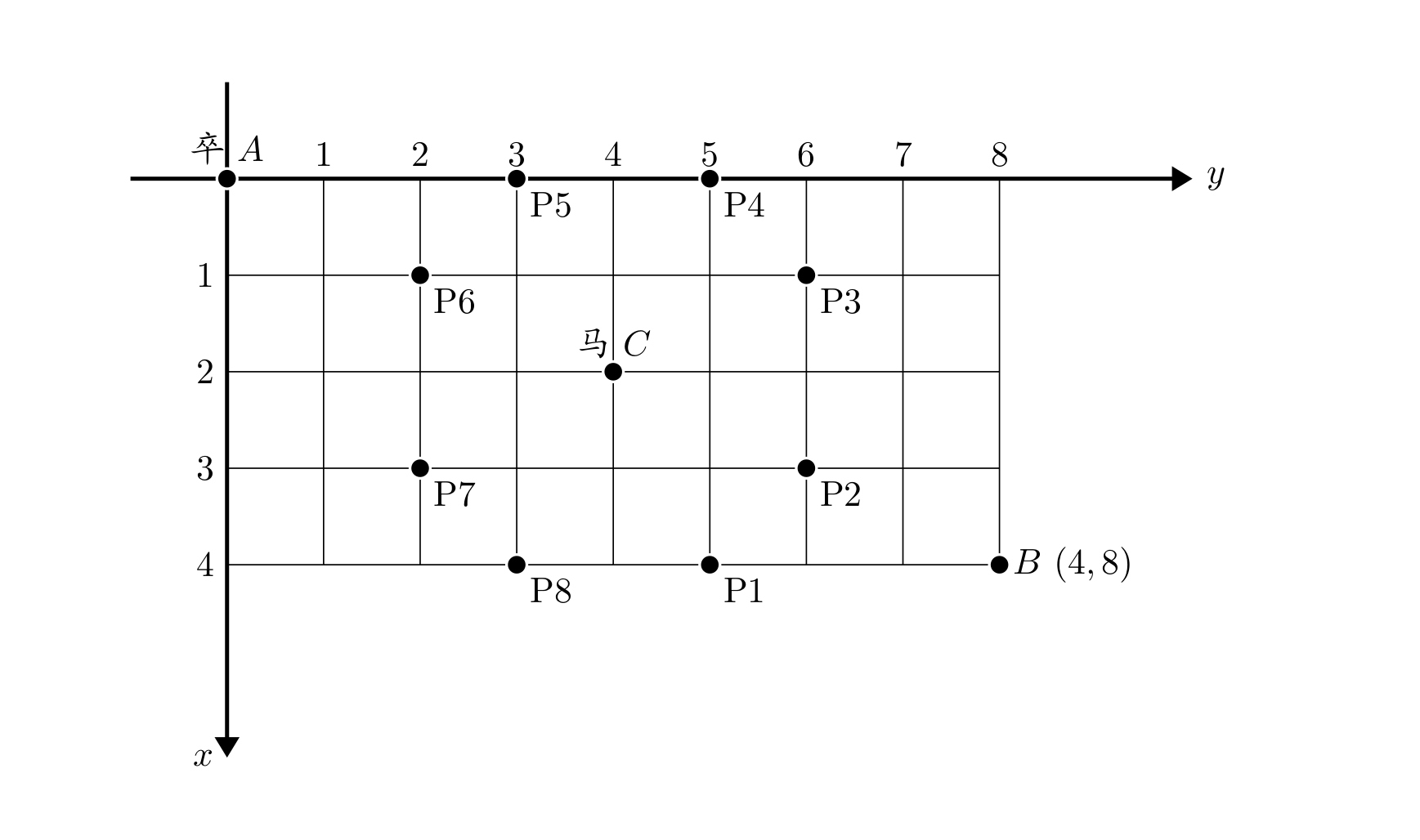
棋盘上 A 点有一个过河卒,需要走到目标 B 点。卒行走的规则:可以向下、或者向右。同时在棋盘上 C 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示,A 点 (0,0)、B 点 (n,m),同样马的位置坐标是需要给出的。
现在要求你计算出卒从 A 点能够到达 B 点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。
输入格式
一行四个正整数,分别表示 B 点坐标和马的坐标。
输出格式
一个整数,表示所有的路径条数。
输入输出样例
输入 #1复制
6 6 3 3输出 #1复制
6说明/提示
对于 100% 的数据,1≤n,m≤20,0≤马的坐标≤20。
【题目来源】
NOIP 2002 普及组第四题
代码加注释:
#include<stdio.h>
#include<string.h>
// 定义一个二维数组dp,用于存储到达每个位置的不同路径数
long long int dp[100][100];
// 定义一个二维数组s,用于标记障碍物位置
bool s[100][100];
int main() {
// 初始化dp数组为0
memset(dp, 0, sizeof(dp));
int x, y, x1, y1;
// 输入起始点和终点坐标
scanf("%d%d%d%d", &x, &y, &x1, &y1);
// 将坐标值加2,这样坐标(1,1)在数组中的位置就是(3,3),以便在数组边界外有空间
x += 2, y += 2, x1 += 2, y1 += 2;
// 定义八个方向的偏移量,用于标记障碍物周围的位置
int next[8][2] = { {1,2},{1,-2},{2,1},{2,-1},{-1,-2},{-2,-1},{-1,2},{-2,1} };
// 将终点标记为障碍物
s[x1][y1] = 1;
// 将终点周围八个方向的位置也标记为障碍物
for (int i = 0; i < 8; i++) {
s[x1 + next[i][0]][y1 + next[i][1]] = 1;
}
// 初始化起点位置到起点的路径数为1
dp[2][1] = 1;
// 动态规划计算到达每个位置的不同路径数
for (int i = 2; i <= x; i++) {
for (int j = 2; j <= y; j++) {
// 如果当前位置是障碍物,则跳过
if (s[i][j]) continue;
// 当前位置的不同路径数等于它左边和上边位置的不同路径数之和
dp[i][j] = dp[i][j - 1] + dp[i - 1][j];
}
}
// 输出从起点到终点的不同路径数
printf("%lld", dp[x][y]);
return 0;
}
//注意:
//代码中使用x += 2, y += 2, x1 += 2, y1 += 2是为了让实际坐标映射到数组dp和s时留有边界空间,
//防止数组越界。
//dp[i][j]保存的是到达位置(i, j)的不同路径数。
//s[i][j]用于标记障碍物位置,其中true表示是障碍物,false表示不是障碍物。
//动态规划过程中,通过累加左边和上边位置的路径数来更新当前位置的路径数。题目2:装箱问题
题目描述
有一个箱子容量为 V,同时有 n 个物品,每个物品有一个体积。
现在从 n 个物品中,任取若干个装入箱内(也可以不取),使箱子的剩余空间最小。输出这个最小值。
输入格式
第一行共一个整数 V,表示箱子容量。
第二行共一个整数 n,表示物品总数。
接下来 n 行,每行有一个正整数,表示第 i 个物品的体积。
输出格式
共一行一个整数,表示箱子最小剩余空间。
输入输出样例
输入 #1复制
24 6 8 3 12 7 9 7输出 #1复制
0说明/提示
对于 100%100% 数据,满足0<n≤301≤V≤20000。
【题目来源】
NOIP 2001 普及组第四题
代码加解析:
#include<stdio.h> // 引入标准输入输出库
#include<iostream> // 引入输入输出流库,但实际上代码中并未使用iostream的功能
using namespace std; // 使用标准命名空间
int a[100]; // 定义一个整型数组a,用于存储n个物品的价值
int dp[20100]; // 定义一个整型数组dp,用于存储容量为j时的最大价值
int main()
{
int V, n; // 定义两个整型变量V和n,分别表示背包的总容量和物品的数量
scanf("%d%d", &V, &n); // 输入背包的总容量V和物品的数量n
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]); // 输入每个物品的价值,并存储在数组a中
}
dp[0] = 0; // 初始化dp数组,当容量为0时,最大价值为0
// 动态规划的主体部分
for (int i = 1; i <= n; i++) { // 遍历每个物品
for (int j = V; j >= a[i]; j--) { // 遍历背包的每个可能容量,从大到小遍历是为了保证每个物品只被选取一次
dp[j] = max(dp[j], dp[j - a[i]] + a[i]); // 更新dp数组,如果当前物品能放入背包并且加上当前物品后的总价值更大,则更新dp[j]
}
}
printf("%d", V - dp[V]); // 输出剩余容量,即总容量V减去最大价值dp[V],即表示背包装不下的物品总价值
return 0; // 主函数返回0,表示程序正常结束
}题目3:小A点菜
题目背景
uim 神犇拿到了 uoi 的 ra(镭牌)后,立刻拉着基友小 A 到了一家……餐馆,很低端的那种。
uim 指着墙上的价目表(太低级了没有菜单),说:“随便点”。
题目描述
不过 uim 由于买了一些书,口袋里只剩 M 元 (M≤10000)。
餐馆虽低端,但是菜品种类不少,有 N 种 ((N≤100),第 i 种卖 ai 元 (ai≤1000)。由于是很低端的餐馆,所以每种菜只有一份。
小 A 奉行“不把钱吃光不罢休”,所以他点单一定刚好把 uim 身上所有钱花完。他想知道有多少种点菜方法。
由于小 A 肚子太饿,所以最多只能等待 11 秒。
输入格式
第一行是两个数字,表示 N 和 M。
第二行起 N 个正数 ai(可以有相同的数字,每个数字均在 10001000 以内)。
输出格式
一个正整数,表示点菜方案数,保证答案的范围在 int 之内。
输入输出样例
输入 #1复制
4 4 1 1 2 2输出 #1复制
3说明/提示
2020.8.29,增添一组 hack 数据 by @yummy
代码加详细解析:
#include<stdio.h>
// 定义两个数组,a用于存储菜品的价格,dp用于存储动态规划的状态
int a[200];
int dp[200][10000];
int main()
{
int n, m;
scanf("%d%d", &n, &m); // 输入菜品的种类数n和拥有的钱数m
// 读取每种菜品的价格
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
// 初始化dp数组,dp[0][0]表示没有菜品可选且钱数为0时的方法数为1(不选任何菜品)
dp[0][0] = 1;
// 动态规划的主体部分
for (int i = 1; i <= n; i++) { // 遍历每种菜品
for (int j = 0; j <= m; j++) { // 遍历当前拥有的钱数
// 如果当前钱数大于菜品价格
if (j >= a[i]) {
// 则可以选择购买当前菜品,方法数等于不购买当前菜品的方法数加上购买当前菜品后剩余钱数的方法数
dp[i][j] = dp[i - 1][j] + dp[i - 1][j - a[i]];
} else {
// 如果当前钱数小于菜品价格,则不能购买当前菜品,方法数等于不购买当前菜品的方法数
dp[i][j] = dp[i - 1][j];
}
}
}
// 输出在拥有m元钱时,可以选择的菜品组合方法数
printf("%d", dp[n][m]);
return 0;
}题目会隔几天更新一次,一直到对这个知识点熟练为止。