吴恩达机器学习-可选实验室：简单神经网络（Simple Neural Network）

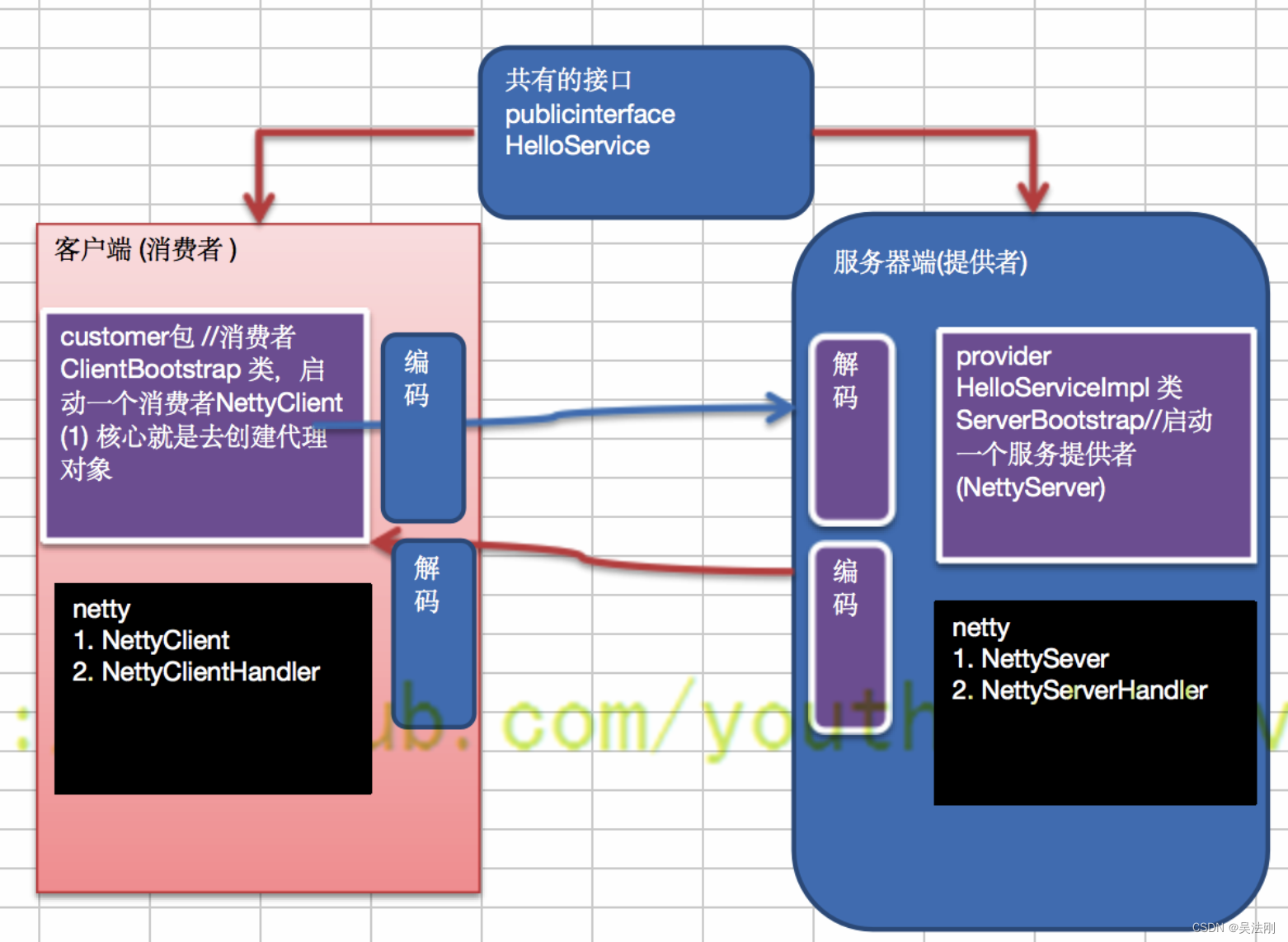
在这个实验室中，我们将使用Tensorflow构建一个小型神经网络
在这里插入图片描述

import numpy as np
import matplotlib.pyplot as plt
plt.style.use('./deeplearning.mplstyle')
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from lab_utils_common import dlc
from lab_coffee_utils import load_coffee_data, plt_roast, plt_prob, plt_layer, plt_network, plt_output_unit
import logging
logging.getLogger("tensorflow").setLevel(logging.ERROR)
tf.autograph.set_verbosity(0)

数据集

X,Y = load_coffee_data();
print(X.shape, Y.shape)

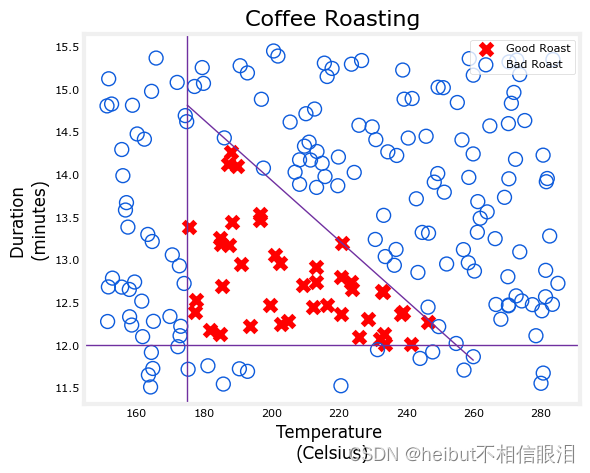
让我们在下面绘制咖啡烘焙数据。这两个功能是以摄氏度为单位的温度和以分钟为单位的持续时间。在家烤咖啡建议时间最好保持在12到15分钟之间，而温度应该在175到260摄氏度之间。当然，随着温度的升高，持续时间应该会缩短。

plt_roast(X,Y)

在这里插入图片描述

标准化数据

如果数据被标准化，将权重与数据拟合（反向传播，将在下周的讲座中介绍）将更快地进行。这与您在课程1中使用的过程相同，其中数据中的每个特征都被标准化为具有相似的范围。下面的过程使用Keras规范化层。它有以下步骤：

创建一个“规范化层”。请注意，正如这里所应用的，这不是模型中的层。
“调整”数据。这将学习数据集的均值和方差，并在内部保存这些值。
规范化数据。
将规范化应用于利用所学习模型的任何未来数据是很重要的。

print(f"Temperature Max, Min pre normalization: {np.max(X[:,0]):0.2f}, {np.min(X[:,0]):0.2f}")
print(f"Duration    Max, Min pre normalization: {np.max(X[:,1]):0.2f}, {np.min(X[:,1]):0.2f}")
norm_l = tf.keras.layers.Normalization(axis=-1)
norm_l.adapt(X)  # learns mean, variance
Xn = norm_l(X)
print(f"Temperature Max, Min post normalization: {np.max(Xn[:,0]):0.2f}, {np.min(Xn[:,0]):0.2f}")
print(f"Duration    Max, Min post normalization: {np.max(Xn[:,1]):0.2f}, {np.min(Xn[:,1]):0.2f}")

在这里插入图片描述
平铺/复制我们的数据以增加训练集大小并减少训练时期的数量。

Xt = np.tile(Xn,(1000,1))
Yt= np.tile(Y,(1000,1))   
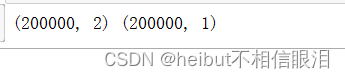
print(Xt.shape, Yt.shape)

Tensorflow模型

Model
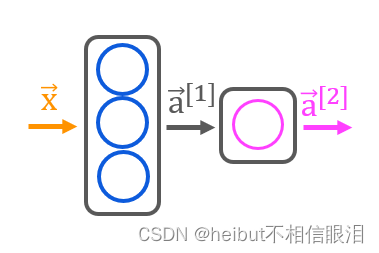
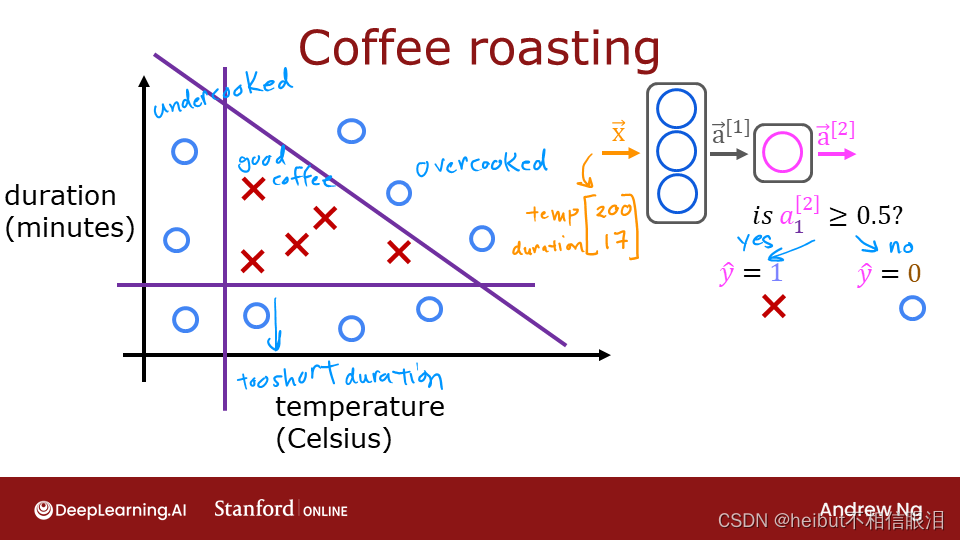
在这里插入图片描述
让我们构建讲座中描述的“咖啡烘焙网络”。有两层Sigmoid激活，如下所示：

tf.random.set_seed(1234)  # applied to achieve consistent results
model = Sequential(
    [
        tf.keras.Input(shape=(2,)),
        Dense(3, activation='sigmoid', name = 'layer1'),
        Dense(1, activation='sigmoid', name = 'layer2')
     ]
)

注1：tf.keras.input（shape=（2，）），指定输入的预期形状。这允许Tensorflow在这一点上调整权重和偏置参数的大小。这在探索Tensorflow模型时非常有用。在实践中可以省略此语句，当在model.fit语句中指定输入数据时，Tensorflow将调整网络参数的大小。
注2：在最后一层中包括S形激活不被视为最佳实践。相反，它会被计入损失中，从而提高数值稳定性。这将在稍后的实验室中进行更详细的描述。

model.summary()

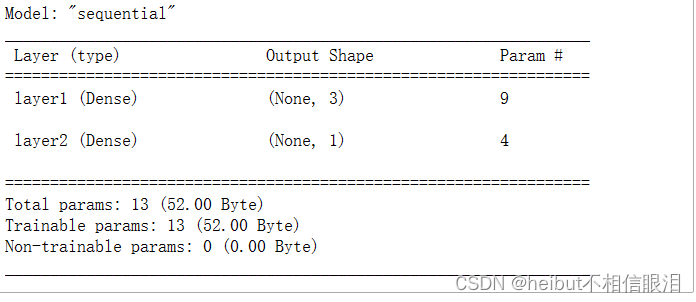
在这里插入图片描述
👆摘要中显示的参数计数对应于如下所示的权重和偏置阵列中的元素数量。

L1_num_params = 2 * 3 + 3   # W1 parameters  + b1 parameters
L2_num_params = 3 * 1 + 1   # W2 parameters  + b2 parameters
print("L1 params = ", L1_num_params, ", L2 params = ", L2_num_params  )

在这里插入图片描述
让我们检查一下Tensorflow实例化的权重和偏差。重量𝑊应具有一定的大小（输入中的特征数量、层中的单元数量），而偏差𝑏大小应与图层中的单位数相匹配：

在具有3个单元的第一层中，我们期望W的大小为（2,3），并且𝑏 应该具有3个元素。
在具有1个单元的第二层中，我们预计W的大小为（3,1），并且𝑏 应该有1个元素。

W1, b1 = model.get_layer("layer1").get_weights()
W2, b2 = model.get_layer("layer2").get_weights()
print(f"W1{W1.shape}:\n", W1, f"\nb1{b1.shape}:", b1)
print(f"W2{W2.shape}:\n", W2, f"\nb2{b2.shape}:", b2)

在这里插入图片描述
以下陈述将在第2周进行详细描述。目前：
model.compile语句定义了一个损失函数并指定了一个编译优化。
model.fit语句运行梯度下降，并将权重与数据相匹配。

model.compile(
    loss = tf.keras.losses.BinaryCrossentropy(),
    optimizer = tf.keras.optimizers.Adam(learning_rate=0.01),
)

model.fit(
    Xt,Yt,            
    epochs=10,
)

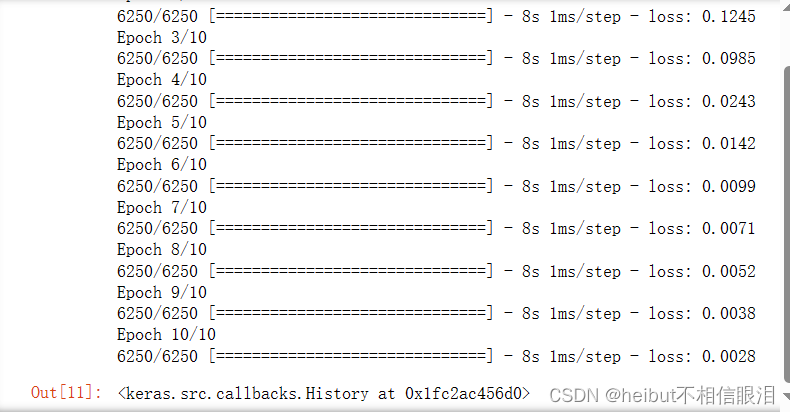
在这里插入图片描述
更新的权重
拟合后，权重已更新：

W1, b1 = model.get_layer("layer1").get_weights()
W2, b2 = model.get_layer("layer2").get_weights()
print("W1:\n", W1, "\nb1:", b1)
print("W2:\n", W2, "\nb2:", b2)

在这里插入图片描述
接下来，我们将加载一些从之前的训练中保存下来的权重。这是为了让这款笔记本在Tensorflow随时间变化时保持稳健。不同的训练跑可能会产生一些不同的结果，下面的讨论适用于特定的解决方案。请随时重新运行已注释掉此单元格的笔记本，以查看差异。

W1 = np.array([
    [-8.94,  0.29, 12.89],
    [-0.17, -7.34, 10.79]] )
b1 = np.array([-9.87, -9.28,  1.01])
W2 = np.array([
    [-31.38],
    [-27.86],
    [-32.79]])
b2 = np.array([15.54])
model.get_layer("layer1").set_weights([W1,b1])
model.get_layer("layer2").set_weights([W2,b2])

👆解释：

在机器学习中，模型的训练过程是一个迭代优化的过程，通过不断调整模型参数使得模型在训练数据上表现更好。在每次训练迭代中，通过计算损失函数关于参数的梯度，我们可以知道当前参数的变化方向，然后根据梯度下降算法来更新参数。
现在来解释一下如何理解这个过程：

随机初始化参数：在开始训练之前，我们通常会随机初始化模型参数。这样做是因为初始参数对模型性能有很大影响，随机初始化可以避免模型陷入局部最优解。
计算梯度：在每次训练迭代中，通过前向传播计算损失函数，然后反向传播计算损失函数关于参数的梯度。梯度告诉我们当前参数的变化方向，即损失函数下降最快的方向。
参数更新：根据梯度下降算法，我们将当前参数沿着负梯度方向进行一定步长的更新。学习率控制了参数更新的速度，较大的学习率可能导致参数更新过大而错过最优值，而较小的学习率可能导致收敛速度过慢。
循环迭代：重复以上步骤，直到达到停止条件（如达到最大迭代次数、损失函数收敛等）为止。

由于训练数据的随机性、模型的复杂性以及训练过程中可能存在的噪声等因素，即使使用相同的初始参数和相同的训练数据，每次训练得到的最终参数可能会有所不同。这种差异是正常的，而且可以通过一些技术手段来提高模型的稳定性和收敛性。

预测
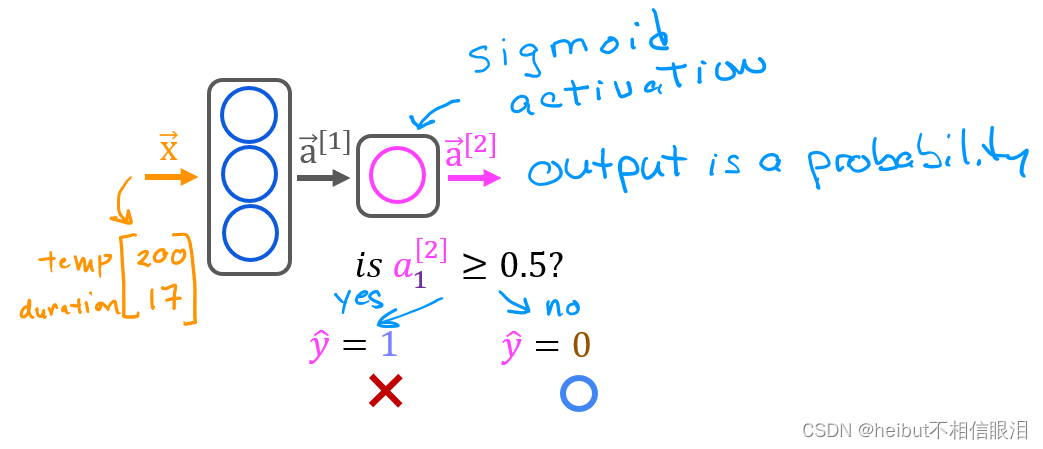
在这里插入图片描述
一旦你有了一个经过训练的模型，你就可以用它来进行预测。回想一下，我们模型的输出是一个概率。在这种情况下，烤得好的概率。要做出决定，必须将概率应用于阈值。在这种情况下，我们将使用0.5

👇 让我们从创建输入数据开始。模型期望一个或多个例子，其中例子在矩阵的行中。在这种情况下，我们有两个特征，所以矩阵将是（m，2），其中m是例子的数量。回想一下，我们已经标准化了输入特征，所以我们也必须标准化我们的测试数据。
要进行预测，请应用预测方法。

X_test = np.array([
    [200,13.9],  # postive example
    [200,17]])   # negative example
X_testn = norm_l(X_test)
predictions = model.predict(X_testn)
print("predictions = \n", predictions)

在这里插入图片描述
Epochs and batches
在上面的编译语句中，epochs的数量设置为10。这规定了整个数据集应在训练期间应用10次。在培训过程中，您可以看到描述培训进度的输出，如下所示：

Epoch 1/10 6250/6250【=========================】-6s

910us/step-loss：0.1782
第一行Epoch 1/10描述了模型当前运行的历元。为了提高效率，训练数据集被分解为“批”。Tensorflow中批次的默认大小为32。在我们的扩展数据集中有200000个示例或6250个批次。第二行6250/6250[====上的注释描述了已执行的批次。

👇为了将概率转换为决策，我们应用了一个阈值：

yhat = np.zeros_like(predictions)
for i in range(len(predictions)):
    if predictions[i] >= 0.5:
        yhat[i] = 1
    else:
        yhat[i] = 0
print(f"decisions = \n{yhat}")

在这里插入图片描述
这可以更简洁地完成：

yhat = (predictions >= 0.5).astype(int)
print(f"decisions = \n{yhat}")

在这里插入图片描述
图层功能
让我们检查一下这些单元的功能，以确定它们在咖啡烘焙决策中的作用。我们将为所有输入值（持续时间、温度）绘制每个节点的输出。每个单元都是一个逻辑函数，其输出范围可以从零到一。图形中的着色表示输出值。

注：在实验室中，我们通常从零开始计数，而讲座可能从1开始。

plt_layer(X,Y.reshape(-1,),W1,b1,norm_l)

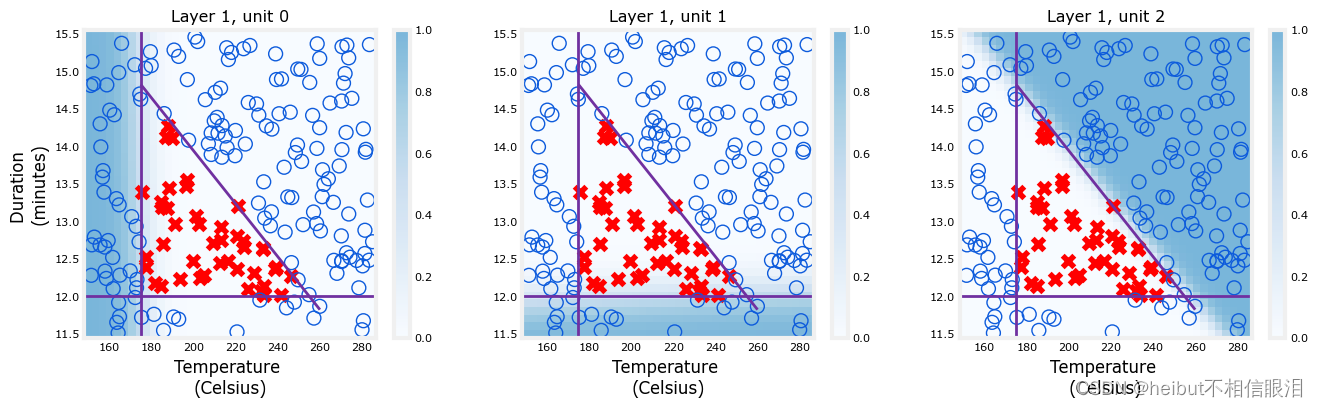
在这里插入图片描述
阴影显示每个单元负责不同的“坏烤”区域。当温度过低时，单位0具有较大的值。当持续时间太短时，第一单元的值较大，而对于时间/温度的不良组合，第二单元的值较大。值得注意的是，网络通过梯度下降过程自行学习这些函数。它们与一个人做出相同决定时可能选择的功能非常相似。

最后一层的函数图有点难以可视化。它的输入是第一层的输出。我们知道第一层使用Sigmoid，所以它们的输出范围在0到1之间。我们可以创建一个三维图来计算三个输入的所有可能组合的输出。如下所示。上面，高输出值对应于“坏烤”区域。下面，最大输出在区域中，其中三个输入是对应于“好烤”区域的小值。
plt_output_u

plt_output_unit(W2,b2)

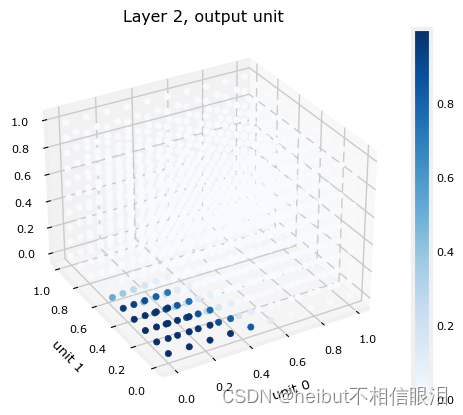
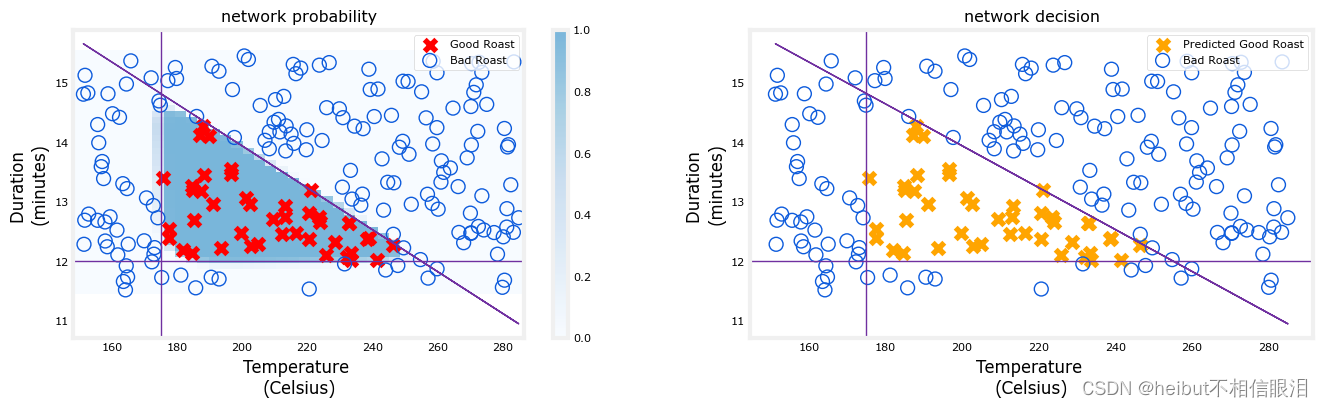
在这里插入图片描述
最后一张图显示了整个网络的运行情况。
左边的图形是由蓝色着色表示的最终层的原始输出。这覆盖在由X和O表示的训练数据上。
右图是在决策阈值之后网络的输出。这里的X和O对应于网络做出的决策。
以下内容需要运行一段时间

netf= lambda x : model.predict(norm_l(x))
plt_network(X,Y,netf)

在这里插入图片描述

祝贺

您已经在Tensorflow中构建了一个小型神经网络。该网络展示了神经网络通过在多个单元之间划分决策来处理复杂决策的能力。