遗传算法

遗传算法概念

遗传算法的概念是在 1975 年由密切根大学的 J.Holland 提出的，这是一种通过模拟自然进化过程寻找最优解的方法。它遵循达尔文的物竞天择，适者生存的进化准则。基本思想：

初始一个种群，选择种群中适应度高的个体进行交叉变异。然后再将适应度低的个体淘汰，留下适应度高的个体进行繁殖，这样不断的进化，最终留下的都是优秀的个体。

基因和染色体

在遗传算法中，我们首先需要将要解决的问题映射成一个数学问题，也就是所谓的数学建模，那么这个问题的一个可行解即被称为一条染色体或个体。如：

3x+4y+5z<100

[1,2,3]，[2,3,4]，[3,2,1]均为这个函数的可行解，这些可行解在遗传算法中均被称为染色体，每一个元素就被称为染色体上的一个基因。

染色体编码与解码

遗传算法的运算对象是表示染色体的符号串，所以必须把变量 x，y，z 编码为一种符号串。常见的编码方式如用无符号二进制整数来表示。解码即将二进制整数转换回最初的表现型。

编码： 5 --> 0101。

解码： 0101 --> 5。

初始群体的产生

遗传算法是对群体进行的进化操作，需要给其准备一些表示起始搜索点的初始群体数据。假如群体规模的大小取为 4，即群体由 4 个染色体组成，每个染色体可通过随机方法产生。

如： 011101 ， 101011 ， 011100 ， 111001。

物竞天择

适应度函数：遗传算法中以染色体适应度的大小来评定各个染色体的优劣程度，从而决定其遗传机会的大小。

选择函数：自然界中，越适应的个体就越有可能繁殖后代。但是也不能说适应度越高的就肯定后代越多，只能是从概率上来说更多。常用的选择方法有轮盘赌选择法。

若表示每个染色体的适应度，则每个个体遗传下来的概率为：

由公式可以看出，适应度越高，则遗传下来的概率就越大，好比赌轮盘，轮盘上所占面积越大，则被小球滚到的概率就越大。

交叉与变异

交叉是遗传算法中产生新的个体的主要操作过程，以一定的概率决定个体间是否进行交叉操作。

如上图为父辈染色体进过交叉后产生新的染色体的过程。

变异为另一种产生新个体的操作，它可以为种群带来多样性：

也就是将我的染色体中的基因，随机的由0变成1，或1变成0。

遗传算法流程

初始化种群
计算适应度
选择适应度高的个体
通过交叉变异选择新的染色体
终止进化

使用python实现遗传算法。

本关任务是使用遗传算法求解目标函数最大值，首先需要随机产生很多个解，即初始化种群，代码如下：

#初始化种群
pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE)) 
# Size函数需要传入两个参数 POP_SIZE为解的个数，即染色体个数。DNA_SIZE为染色体长度

其中POP_SIZE为解的个数，即染色体个数。DNA_SIZE为染色体长度。

由于染色体为二进制编码，所以还需要将二进制转换为浮点数的解码方法：

#解码
def translateDNA(pop): 
    return pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2**DNA_SIZE-1) * X_BOUND[1]

上述代码中： pop.dot(2 ** np.arange(DNA_SIZE)[ : : -1])已经转换成十进制但是需要归一化到 0~5 ，如有 1111 这么长的 DNA,要产生的十进制数范围是 [0, 15] ，而所需范围是 [-1, 1] ，就将 [0,15] 缩放到 [-1,1] 这个范围。

a[ : : -1]相当于a[-1:-len(a)-1:-1]，也就是从最后一个元素到第一个元素复制一遍。所以你看到一个倒序，np.arange(DNA_SIZE)[ : : -1]得到 10,9,8,...,0 。

如将 10101 转换到 0 到 5 之间：

然后计算每个染色体的适应度，由于是求解最大值，函数值越大则越应该被选择，所以，将每个染色体对应的函数值减去最小值作为适应度：

#获取染色体适应度
def get_fitness(pred): 
    return pred + 1e-3 - np.min(pred)

再选择适应度高的染色体：

#选择适应度高的染色体
def select(pop, fitness):    
    idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
                           p=fitness/fitness.sum())
    return pop[idx]

再对染色体进行交叉变异操作：

#交叉
def crossover(parent, pop):     
    if np.random.rand() < CROSS_RATE:
        i_ = np.random.randint(0, POP_SIZE, size=1)                             
        cross_points = np.random.randint(0, 2, size=DNA_SIZE).astype(np.bool)   
        parent[cross_points] = pop[i_, cross_points]                            
    return parent
#变异
def mutate(child):
    for point in range(DNA_SIZE):
        if np.random.rand() < MUTATION_RATE:
            child[point] = 1 if child[point] == 0 else 0
    return child

总流程如下：

def F(x): return np.sin(10*x)*x + np.cos(2*x)*x
def ga(F):
    '''
    F:需要求解的函数
    '''
    #初始化种群
    pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE))
    #开始进化
    for _ in range(N_GENERATIONS):
        #计算函数值
        F_values = F(translateDNA(pop))
        #计算适应度
        fitness = get_fitness(F_values)
        #选择适应度高的个体
        pop = select(pop, fitness)
        pop_copy = pop.copy()
        #通过交叉变异选择新的染色体
        for parent in pop:
            #交叉产生子代
            child = crossover(parent, pop_copy)
            #变异产生子代
            child = mutate(child)
            #子代代替父代
            parent[:] = child
    #获取最优解
    x = translateDNA(pop)[-1]
    return x

其中：

N_GENERATIONS为进化轮数。
CROSS_RATE为交叉概率。
MUTATION_RATE 为变异概率。
X_BOUND 为函数定义域。

具体例子

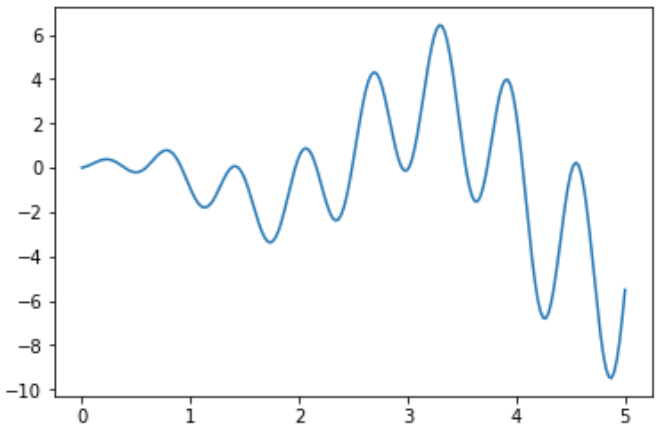
实现遗传算法。并求解函数f(x)在区间 [0,5] 上的最大值:

函数图像如下：

#encoding=utf8
import numpy as np
DNA_SIZE = 10   
POP_SIZE = 100         
CROSS_RATE = 0.8         
MUTATION_RATE = 0.003    
N_GENERATIONS = 500
X_BOUND = [0, 5] 
#获取染色体适应度
def get_fitness(pred): 
    return pred + 1e-3 - np.min(pred)
#解码
def translateDNA(pop): 
    return pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2**DNA_SIZE-1) * X_BOUND[1]
#选择适应度高的染色体
def select(pop, fitness):    
    idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
                           p=fitness/fitness.sum())
    return pop[idx]
#交叉
def crossover(parent, pop):     
    if np.random.rand() < CROSS_RATE:
        i_ = np.random.randint(0, POP_SIZE, size=1)                             
        cross_points = np.random.randint(0, 2, size=DNA_SIZE).astype(np.bool)   
        parent[cross_points] = pop[i_, cross_points]                            
    return parent
#变异
def mutate(child):
    for point in range(DNA_SIZE):
        if np.random.rand() < MUTATION_RATE:
            child[point] = 1 if child[point] == 0 else 0
    return child
def ga(F):
    '''
    F:需要求解的函数
    x:最优解
    '''
    #初始化种群
     # 初始化种群（随机生成二进制染色体）
    pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE))
    #开始进化
    for _ in range(N_GENERATIONS):
        #计算函数值
        F_values = F(translateDNA(pop))
        #计算适应度
        fitness = get_fitness(F_values)
        #选择适应度高的个体
        pop = select(pop, fitness)
        pop_copy = pop.copy()
        #通过交叉变异选择新的染色体
        for parent in pop:
            #交叉产生子代
            child = crossover(parent, pop_copy)
            #变异产生子代
            child = mutate(child)
            #子代代替父代
            parent[:] = child
    #获取最优解
    x = translateDNA(pop)[-1]
    return x