服务器上的433 ssl证书,可以让网站以https加密方式访问,但是这个证书会占用443端口,iis7版本,只能安装一个443证书,所以.原来的过期了.需要删除.删除方式,不是进运行 win+r的mmc 而是进iis的默认的总的主页面板(不是点击具体的网站或者程序池),点击服务器证书.进去才能删除.否则.安装新证书.可能识别不了.如下图

.iis8及以上版本可以在一台服务器上.对运行了多个独立域名的网站.安装多个443证书.原教程地址.
https://www.52help.net/domain/384.html
根据教程.如果有两个网站,需要其中一个网站,默认选择对应的证书即可,服务器名称指示那里不需要打钩.主机名也不用填
第二个或第三个站,则需要选择证书,同时填主机名,名称指示也要打钩
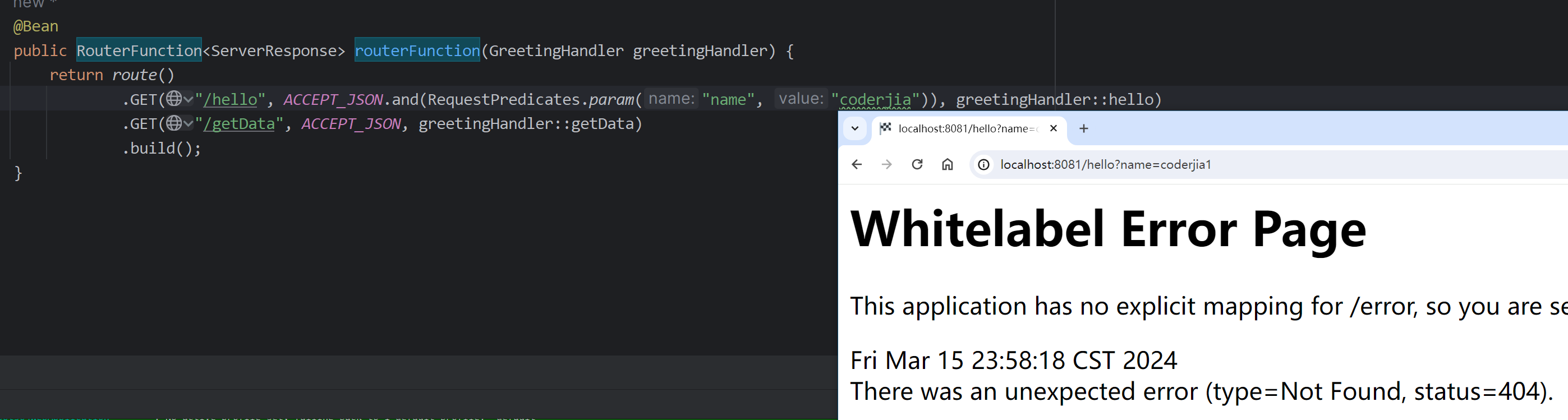
另外,网站不但要绑定443端口,同时也要绑定80端口,然后,做 一下301重定向跳转.如果通过网站代码的形式跳转.参考这个教程
https://blog.csdn.net/viqecel/article/details/136716663