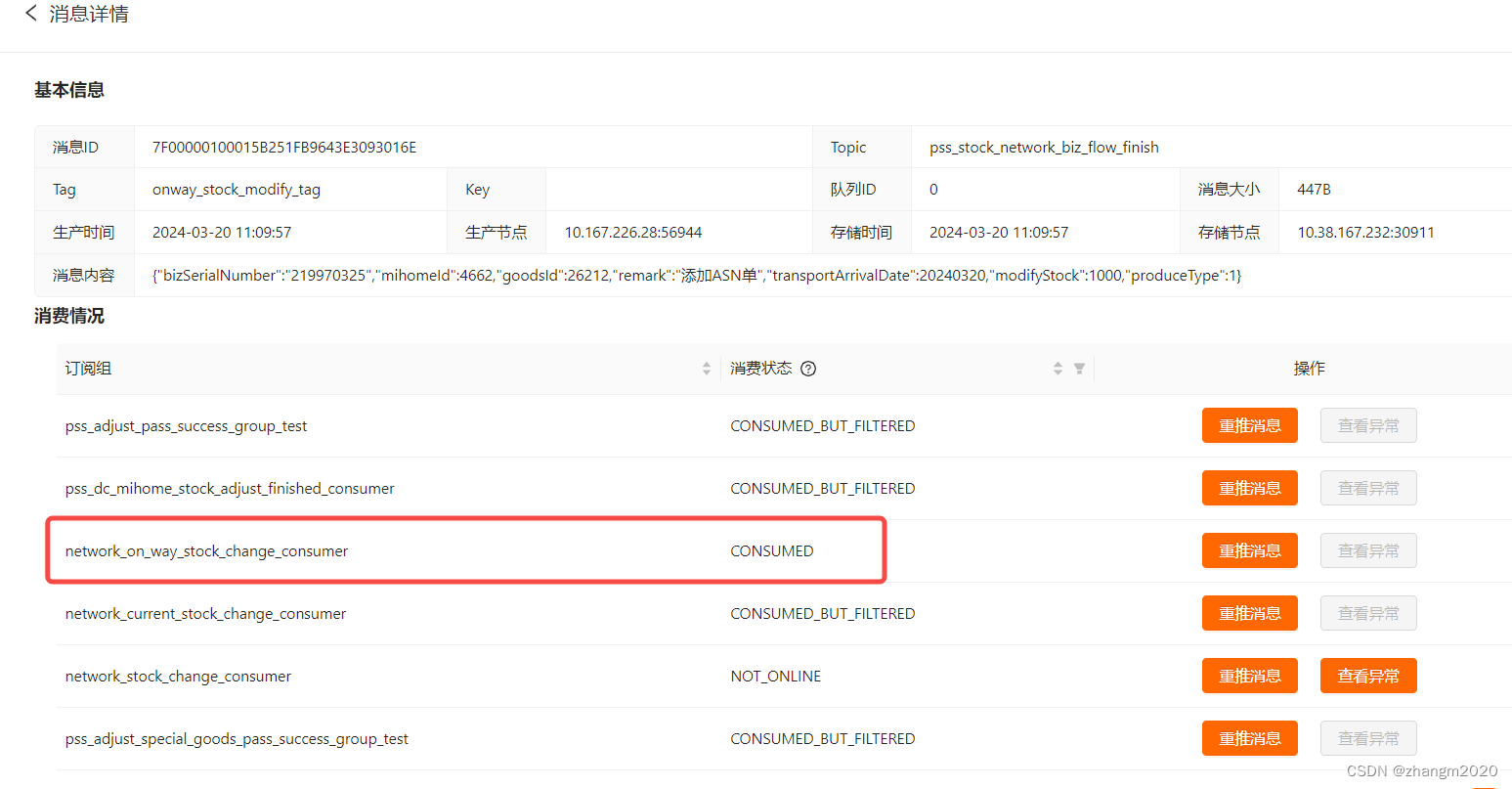
解法：

假设编号从左到右递增，奶牛每次只能去往左边的牛圈。因此等分最大奶牛数小于等于最右边牛圈奶牛数，不妨设数为k，那么a[i]>=k，a[i-1]>=2k。。。

做后缀和+二分答案就可找到k

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
#define endl '\n'
bool check(vector<int>& ne, int k) {
	int n = 1;
	for (int i = ne.size()-2; ~i; i--) {
		if (ne[i] < n * k) {
			return false;
		}
		else n++;
	}
	return true;
}
int main() {
	int n; cin >> n;
	vector<int> vec(n+1), ne(n+1);
	for (int i = 0; i < n; i++) cin >> vec[i];
	for (int i = n - 1; ~i; i--) ne[i] = vec[i] + ne[i + 1];
	int l = 0, r = vec[n - 1];
	int res = 0;
	while (l <= r) {
		int mid = l + (r - l) / 2;
		if (check(ne, mid)) {
			res = mid;
			l = mid + 1;
		}
		else {
			r = mid - 1;
		}
	}
	long long sum = 0;
	for (int i = n - 1; ~i; i--) {
		if (vec[i] > res) {
			if (i > 0) {
				vec[i - 1] += vec[i] - res;
			}
			sum += vec[i] - res;
		}
	}
	cout << sum << endl;
	return 0;
}

解法二：

#include <iostream>
using namespace std;
int a[100005], b[100005];
int main()
{
    long long n, num = 0, min = 1e9;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    for (int i = n; i >= 1; i--)
        b[i] = a[i] + b[i + 1];
    for (int i = 1, j = n; i <= n; i++, j--) {
        if ((b[i] / j) < min) min = (b[i] / j);
    }
    for (int i = 1, j = n; i <= n; i++, j--) {
        num += abs(b[i] - min * j);
    }
    cout << num;
}