无位置传感器控制,这个方向也是电机控制里面的大热门了。最近在看PLL,中国电机有一篇ESO-PLL获得了23年的高影响力论文,标题如下。因为这篇ESO-PLL需要用到下面这篇英文文献的转子位置观测器,想着就先把这个观测器的文章给复现了。


这篇转子位置的观测,采用了非线性观测器,在知乎上面以及某站上面都有大佬发了相关视频/帖子来解释这篇文章的原理,但是还没人讲讲这篇论文的仿真,我就自己做了个试试。感觉设计的观测器确实挺方便的,模型搭起来也还好,不算麻烦。
无位置系列就打算出这一篇观测器,毕竟我主要是为了学习PLL的,只是顺带复现一下这篇论文。不过下面也把仿真搭建的过程说得比较详细了。
1.非线性磁链观测器的仿真搭建
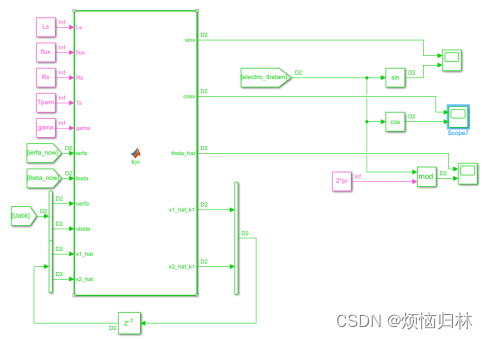
文章先是定义了三个中间x,y,n变量。这里值得注意的是,y里面涉及到了静止坐标系的电压值(也就是U阿尔法以及U贝塔),这个得自己搭建一个模块采集一下这个电压。


接着就可以根据式子(8)估计出中间变量x,伽马(也就是我红色方框画圈的符号),代表的观测器增益,这个伽马只要大于零,观测器就是收敛的。当然,伽马越大就收敛的越快。
当估计出准确的x之后,因为x里面包含sin与cos的关系,就可以根据sin和cos计算出转子位置角度了。

文章里还涉及了观测器的稳定性证明,这里就不用看了,只要会搭这个观测器就行。

先测试一下在不同观测器增益下,观测器的收敛情况吧。(此时还没有把观测器直接用于控制系统里,只是先单独测试一下观测器)
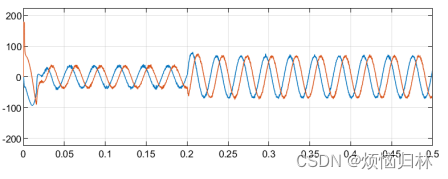
如下图所示,我把自己搭建的模块估计的sin、cos以及电角度的数值拿出来对比看看了。
观测器增益伽马γ分别取1000、5000(论文中取的是8000)。
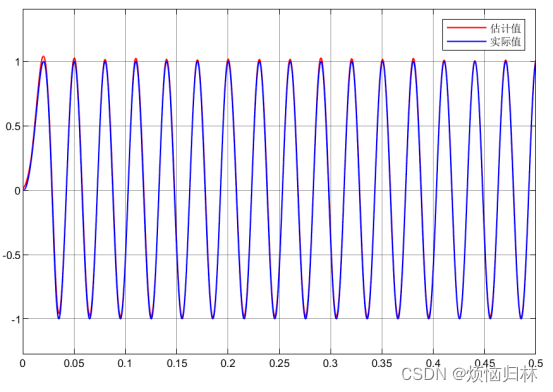
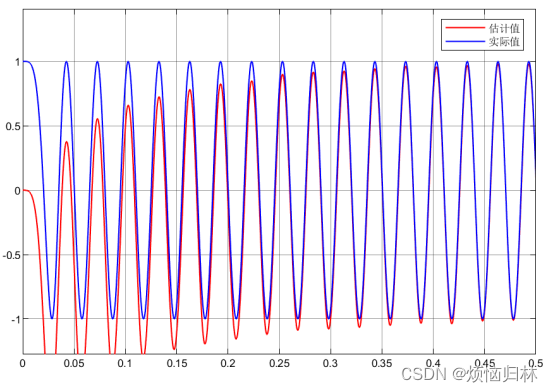
可以看到,sin估计的还是比较准的,但是估计的cos明显有一个缓慢收敛的过程,这说明选择的观测器增益伽马γ还是太小了。
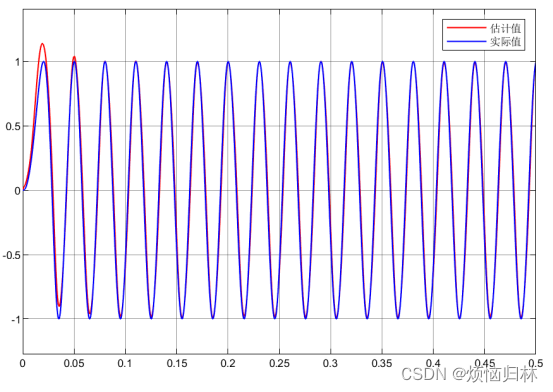
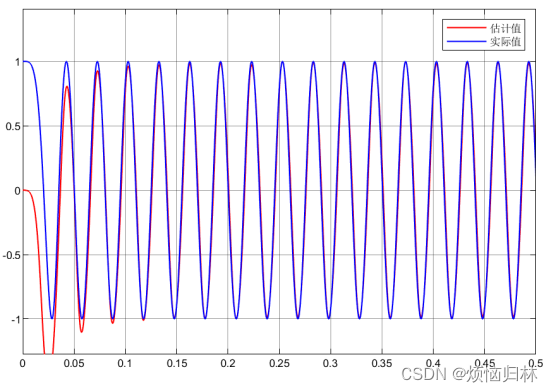
此时的sin和cos的估计值都挺准确的,而且收敛也很快。一开始时,因为转速比较低,所以此时的观测器没办法快速收敛,这也是无位置传感器控制技术在低速段受限的原因。
这里再注意一个点,就是论文中的电角度theta是根据式子(9),利用arctan进行了公式计算。在matlab里面,arctan得到的角度范围是-pi/2到+pi/2(如下图所示),而我们电机控制里面说的角度通常是0到2*pi,所以我们有必要给arctan的输出优化一下。
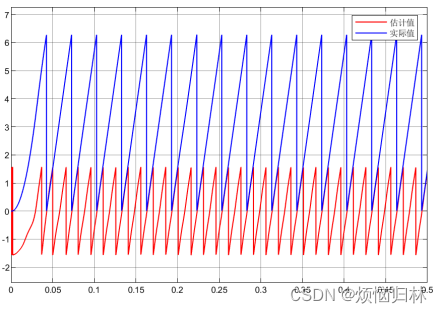
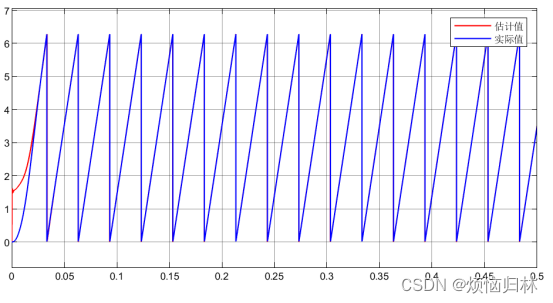
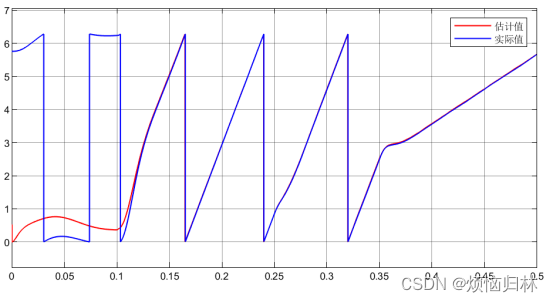
可以看到这个转子位置/磁链观测器的观测效果还是很好的。
即使是在200r/min的时候,估计值和实际值还是基本完全重合,说明这个磁链观测器的观测效果还是非常好的呢。
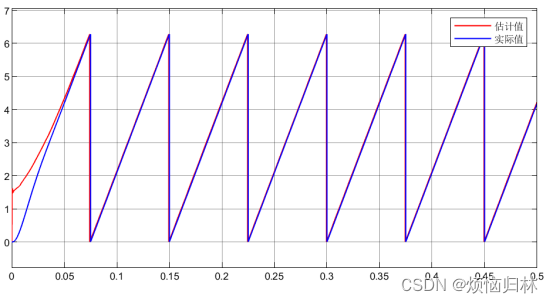
2.锁相环PLL的仿真搭建
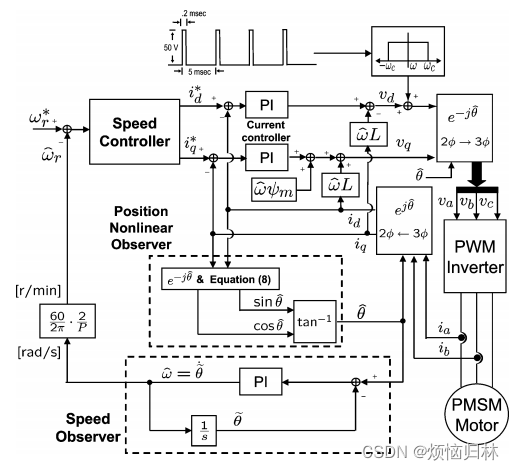
搭建好磁链观测器之后,需要计算速度/转速,这篇英文文献中采用的锁相环PLL是传统的二阶PLL,其原理如下图所示。
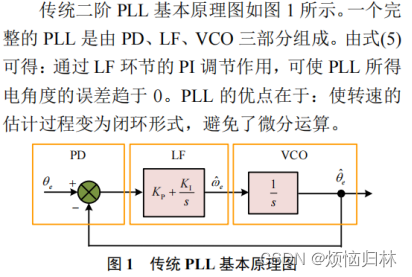
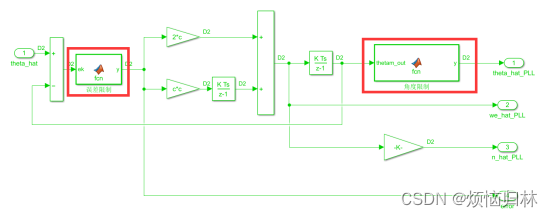
上图是我自己搭建的PLL仿真图,这里值得注意的有两点:
1)在PLL的原理图中可以看到,PLL的输出及估计的电角度,来自于电角速度的积分,如果不进行适当的限幅(将其设置在0到2pi之间),那么其数值将会无限变大。限幅前后的对比如下图所示,蓝线就是没限幅之前的电角度输出。
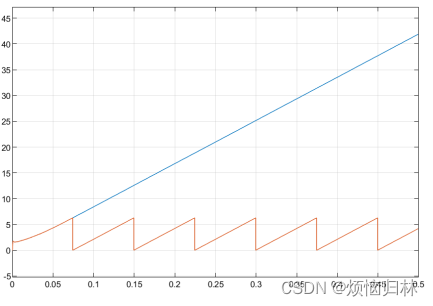
2)角度的误差也要进行一定的处理。这句话是什么意思呢,我下面用几个图来解释。
先把某次电角度从2pi切换到0时的角度数值放大一下。
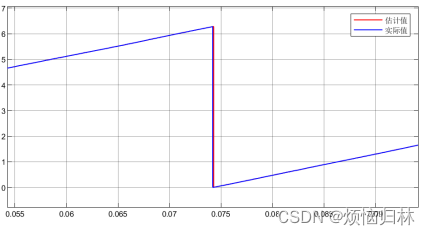
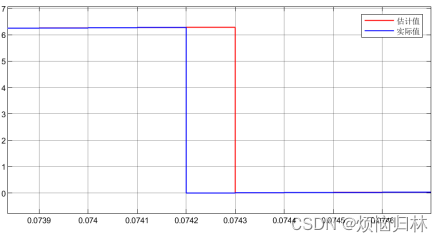
经过两次放大之后我们可以看到,会出现实际值先掉到0然后估计值再掉到0的情况(当然也有可能会出现估计值先掉到0然后实际值再掉到0的情况)。如果这时候不做相应的处理,而是用二者的差值直接相减,会导致此时的误差error为2pi左右,2pi的error经过PI,会导致估计的转速出现极大的波动。就如下图所示,就在电角度切换到0的时候,估计的转速数值非常非常大!实际转速500r/min,而估计转速都超过了1500r/min。
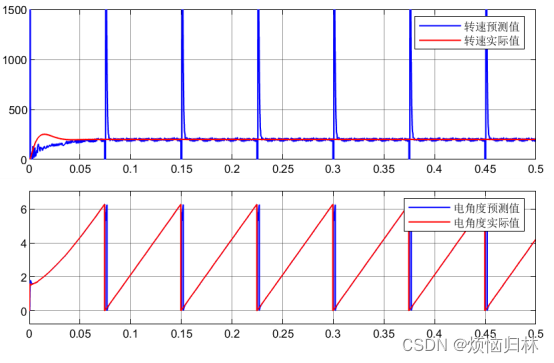
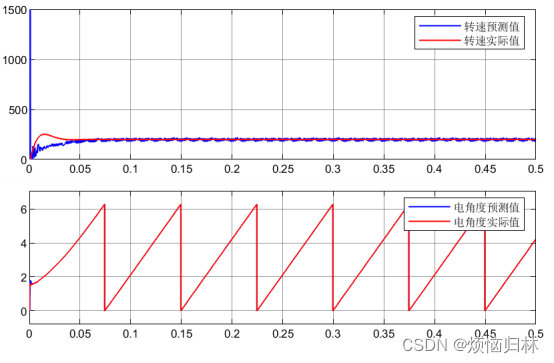
二阶PLL的参数设计为:

3.整体仿真搭建
把PLL和观测器都搭建好了之后,就可以实行整个系统的闭环控制了。
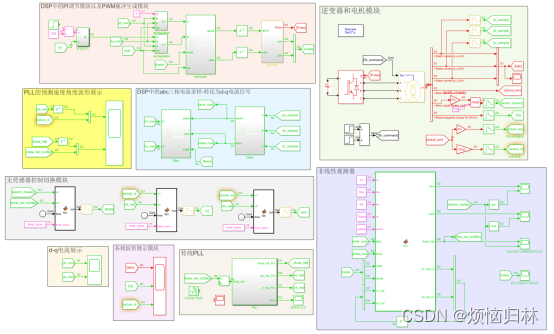
仿真设置:
Tpwm = 1e-4;%开关周期
Tspeed = 1e-4;
Pn = 4;%电机极对数
Ls = 8.5e-3;%定子电感,采用隐极的,Ld=Lq=Ls
Rs = 3;%定子电阻
flux = 0.1688;%永磁体磁链
Vdc = 311;%直流母线电压
iqmax = 20;%额定电流
fc = 200;%电流环带宽
%PLL增益
c = 500;
%位置观测器增益
gama = 9000;
初始给定转速200r/min,0.25s加入10Nm负载,0.35s给定转速改为50r/min
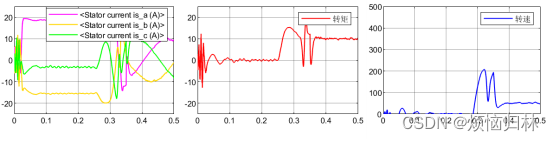
从上面整个图中可以看到,电机没有办法启动,这是因为磁链观测器没有观测到准确的角度。0.25s负载加入之后,负载拖着电机旋转,此时电机开始旋转,观测器能够观测器到准确的电角度了,所以电机最终能够稳定在50r/min了。
3.1低速段d轴电流注入
论文中说,在低速段进行d轴电流注入可以提高低速段观测器的鲁棒性。

那我现在设定一个程序,在低速段(100r/min以内)的d轴电流给定值改为2A。可以看到,低速段注入d轴电流之后,电机能够直接启动了。不论是后来的突加负载,还是减速,性能都是OK的,能够稳定运行。这次启动完全属于瞎猫碰上死耗子,刚好使得观测器收敛了(这点在后面会解释)。
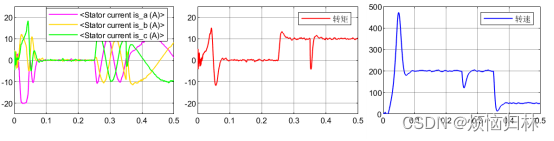
但是注意到,加速到200r/min时,转速的超调量非常大。主要原因就是一开始时,PLL估计的转速不太准。如下图所示。

接下来再看看高速段的表现,初始给定转速500r/min,0.25s加入10Nm负载,0.35s给定转速改为1500r/min。从下面的仿真来看,跑较高的转速的时候,观测器还是没问题的,我们一般还是比较关注低速段的性能。
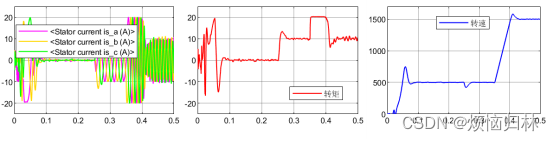

3.3改进的启动措施
再回顾一下这篇英文文献——低速注入d轴电流的方法进行启动。这里有一点值得注意,我仿真中是设置低速时d轴电流参考值为2A。
但是呢,在启动的时候,非线性磁链观测器根本不知道d轴在哪。所以说,我刚才在设置d轴电流参考值为2A之后能够启动,完全属于瞎猫碰上死耗子。
那我们应该怎么样准确的注入d轴电流呢?那最简便的方法就是给让逆变器产生(100)电压矢量,此时会让转子d轴与电机A相轴线对齐,且A相电流为正,BC相电流为负。感兴趣的可以画个矢量图看看,此时d轴电流就是为正咯,然后q轴电流为0。
按照这个思路,我又搭了一个程序。这个程序的意思就是在0.05s之前,阿尔法轴电压给定为20V,贝塔轴电压为0,也就是给逆变器(100)电压矢量的指令了(毕竟阿尔法轴对应的就是A相轴线)。0.05s之后就进行无感启动。这里值得注意的是,这个程序代码里面,给的是20V的U阿尔法参考电压,直流母线电压是311V,所以20V参考电压的话只会产生一个比较小的占空比。所以也不是完全给100,而是相当于给100和000,这样的话,电流就只有几A而已。如果在0.05s前只给100的话,电机很容易过流的。
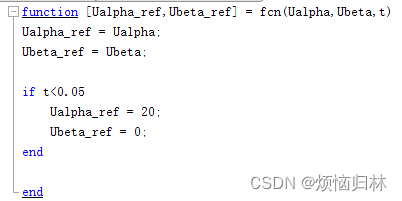
仿真工况:初始给定转速200r/min,0.05s前注入100电压矢量,0.05s正式启动,0.25s加入10Nm负载,0.35s给定转速改为50r/min。
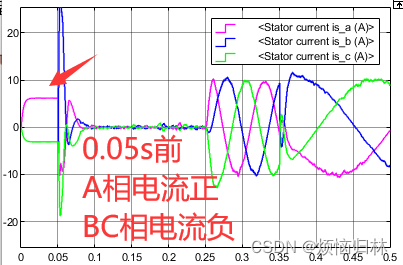
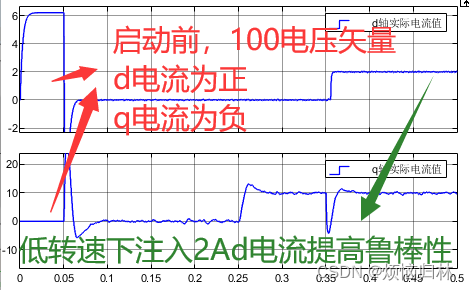
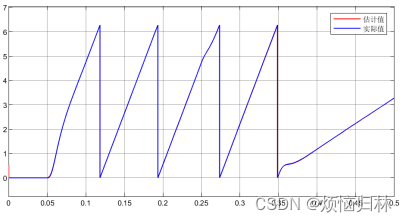
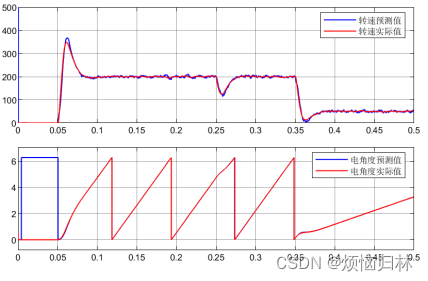
可以看到,采用100电压矢量来产生d轴电流的方法,是非常有效的,能够保证非线性观测器快速收敛以及PLL快速跟随实际转速。
3.3仿真展示
我们再随机选几个初始电角度来看看电机的启动情况:初始电角度30°、60°、90°、130°、160°、290°、330°。在0.1s之前,电压矢量都为100,0.1s后开始启动。
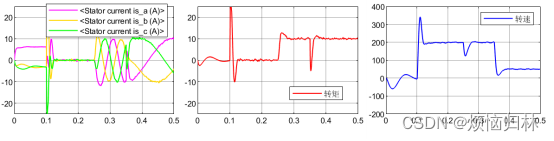
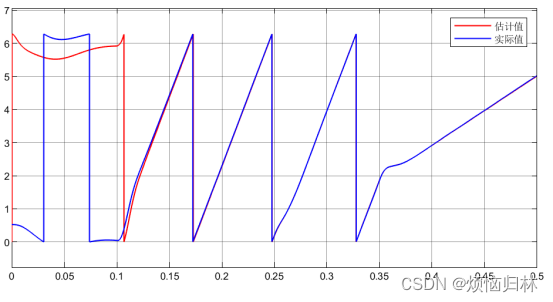
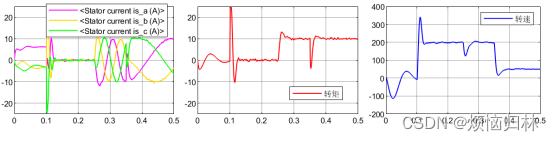
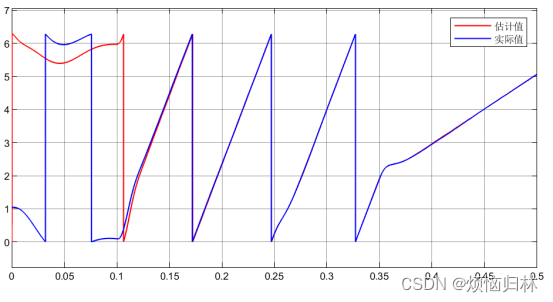
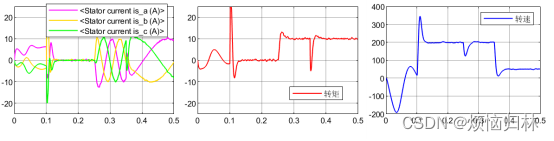
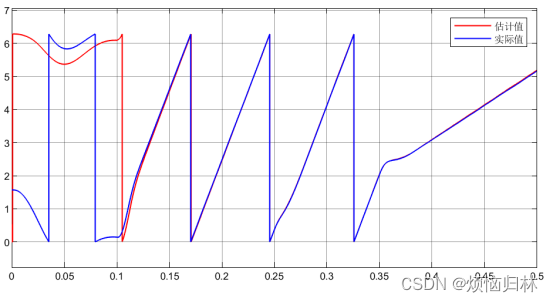
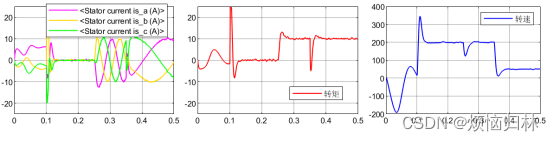
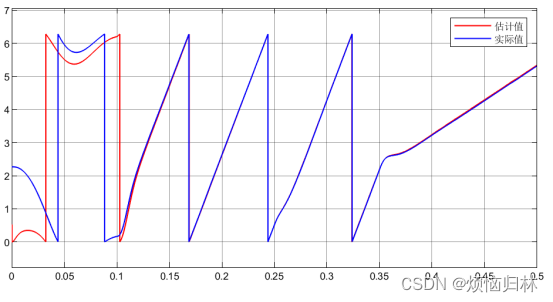
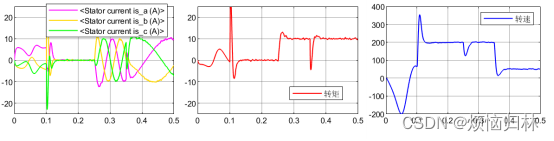
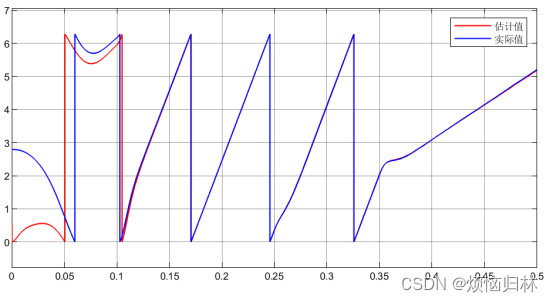
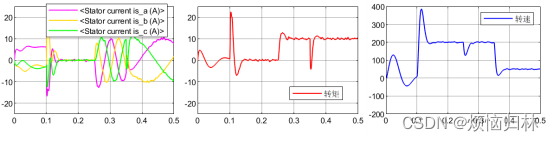
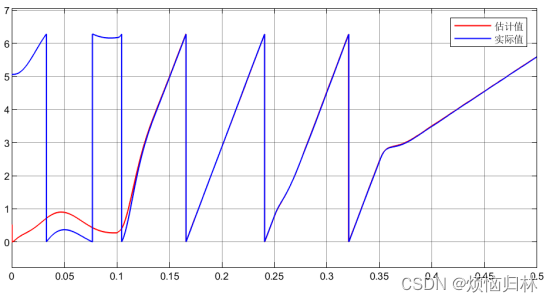
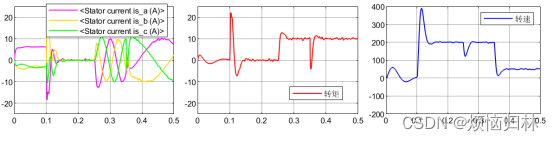
从上述那么多组仿真来看,在所选取的这些电角度的情况下,电机都是可以在0.1s之后达到给定转速200r/min,并且在突加负载以及减速至50r/min的情况下都具有很好的表现。
这个非线性磁链观测器对应的论文也说了,在零转速的情况下,非线性磁链观测器没办法准确观测器转子角度。

而我们在0.1s前作用电压矢量100的话,相当于把d轴拉到A轴上,假如一开始d轴与A轴没有重合,那么转子就会转向A轴,在这个过程中,就有了一定的转速,所以能够使得观测器得到的转子角度接近于真实值。
从上面的仿真也可以看出,在很多情况下,0.1s之前,观测器得到的转子角度都没有完全等于实际的角度,但是其误差都相对比较小了,所以可以启动了。
以上仿真均为个人理解,如有不当之处请见谅。