前言

        这一章主要介绍机器学习在金融领域一个重要应用：客户违约预测模型的搭建，其所用到原理为机器学习中的决策树模型。通过本章的学习，您能了解在信息时代下金融风险控制的新手段，并对机器学习有一个初步的了解。

1. 机器学习在金融领域的应用

说到机器学习（Machine Learning），有的读者可能会感觉比较陌生，然而说到AlphaGo这一击败了世界顶级围棋选手的智能机器人，想必大家多少都有些耳闻。机器学习便是模拟或实现人类的学习行为，以探寻规律或者获得新的技能，机器学习某种程度上可以说是人工智能的核心。

举个简单的例子，如下图所示，该机器学习的目的就是要从一堆散点中寻找到这些散点背后的规律。

        本章主要介绍一下客户违约预测模型，作为机器学习在金融领域应用的典型案例。在传统金融领域，往往存在两方角色，一方为借钱的借款方，另一方则为借钱给别人的贷款方，而作为贷款方则非常关心借款方是否会违约，即借钱不还。有的借款方可能完全就是抱着借钱不还的心态去借的资金，而对于这些客户，则需要搭建一套客户违约预测模型，根据借款人的各方面特征，来训练出合适的模型进行违约概率预测，从而在源头上拒绝这些潜在违约客户。

        可用来搭建客户违约预测模型的方法有很多，如逻辑回归模型、决策树模型、神经网络模型等，这里则使用一个在商业上用的较多的决策树模型。

2. 决策树模型的基本原理

2.1 决策树模型简介

决策树模型是机器学习各种算法模型中比较好理解的一个模型，它的基本原理便是通过对一系列问题进行if/else的推导，最终实现相关决策。

下图便是一个典型的决策树模型，首先判断是否曾经违约：

        以下的决策树模型也是之后我们要搭建的客户违约预测模型的雏形。不过商业实战中不会单纯根据“曾经违约”以及“收入<10,000”两个特征就判断成违约或者非违约，而是根据多个特征来预测违约概率，并根据相应的阈值来判断是否违约，比如违约概率超过50%即认为该用户会违约。 

        这里解释几个决策树模型的重要关键词：根节点、父节点、子节点和叶子节点

        

        决策树模型的关键即是如何选择合适的节点进行分裂。在上图中，最上面的“曾经违约”就是根节点，其中“收入<10,000”则为其子节点，同时也是其下面两个节点的父节点，最后的“违约”及“不违约”则为叶子节点。

        实际应用中，风控人员会通过已有的数据来看违约客户都符合什么样的特征，比如看他们的：

        然后选择合适的特征进行节点分裂，便可以搭建出类似上图所示的决策树模型。利用该决策树模型就可以预测之后其他客户的违约可能性，从而避免潜在风险。

        决策树概念本身并不复杂，主要就是通过连续的逻辑判断来得到最后的结论，其关键的难点在于如何建立出这样一颗树来

        比如根节点应该选择哪一个特征，选“曾经违约”作为根节点和选“收入<10,000”作为根节点会起到不同的效果。其次收入作为一个连续变量，是选“收入<10,000”作为一个节点，还是选“收入<100,000”作为一个节点都是有考究的。

2.2 决策树模型的建树依据

        决策树模型的建树依据主要用到一个基尼系数(gini)的概念。基尼系数用于计算一个系统中的失序现象，也即系统的混乱程度。基尼系数越高，系统混乱程度越高，建立决策树模型的目的就是通过合适的分类来降低系统的混乱程度，其计算公式如下：

其中pi为类别i在样本T中出现的频率，即类别为i的样本占总样本个数的比率。

为∑"为" 求和公式，即把所有的pi^2进行求和。

        举例来说，对于一个全部都是违约客户的样本来说，里面只有一个类别：违约客户，其出现的频率是100%，所以该系统基尼系数为1 - 1^2 = 0，表示该系统没有混乱，或者说该系统的“纯度”很高。

        如果样本里一半是违约客户，另一半是非违约客户，那么类别个数为2，每个类别出现的频率都为50%，所以其基尼系数为1 - （0.5^2 + 0.5^2）= 0.5，也即其混乱程度很高。

       当引入某个用于进行分类的变量（比如“曾经违约”），则分割后的基尼系数公式为：

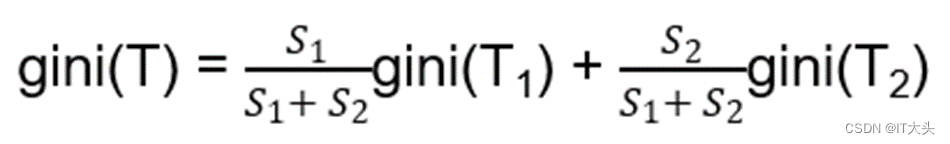
其中S1、S2为划分成两类的样本量，gini(T1)和gini(T2)为划分后的两类各自的基尼系数。

        举例来说，一个初始样本中有1000个客户，其中已知有400人违约，600人不违约，我们希望通过这个样本来搭建一个决策树模型来预测之后的客户违约情况。

        其划分前该系统的基尼系数为1 - (0.4^2 + 0.6^2) = 0.48，可以看到其混乱程度还是挺高的，那么下面采用两种不同的划分方式来决定初始节点：

1. 根据“曾经违约”进行分类

2. 根据“收入<10,000”进行分类

        可以看到不划分的时候系统的基尼系数为0.48，在根据“曾经违约”进行划分后系统的基尼系数为0.3，而根据“收入<10,000”进行划分后系统的基尼系数为0.45。基尼系数越低表示系统的混乱程度越低，能够比较好的作为一个预测模型，所以这里选择“曾经违约”作为第一个节点。这里演示了第一个节点如何进行选择，而第一个节点下面的节点也是用类似的方法来进行选择的 

         对于“收入”这一变量来说，是选择“收入<10,000”还是选择“收入<100,000”来进行划分，也是根据计算在这两种情况下划分后的基尼系数来进行判断。如果还有其他的变量，比如说“年龄”、“性别”等，也是通过类似的手段计算划分后的系统的基尼系数，来看如何进行节点的划分，从而搭建一个较为完善的决策树模型。

3. 实战

文章地址:机器学习之客户违约预测模型搭建之案例实战-CSDN博客