MATLAB：函数与数值积分

一、数学函数图像的绘制

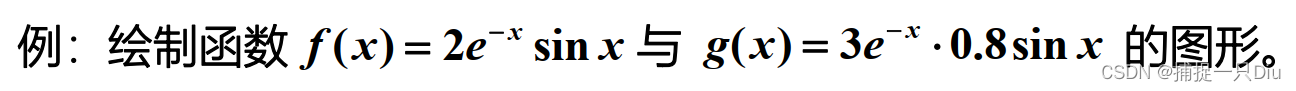
clc,clear
fh = @(x)2*exp(-x).*sin(x);
Xrange = [0,8];
gx = @(x)3*exp(-x)*0.8.*sin(x);
fplot(fh,Xrange,'r-*','LineWidth',1.5)
hold on
grid on 
fplot(gx,Xrange,'b-o','LineWidth',1.5)
axis([-0.5,8.5,-0.1,0.85])
legend('fh = @(x)2*exp(-x).*sin(x)','gx = @(x)3*exp(-x)*0.8.*sin(x)')
legend('boxoff')
title('fplot函数绘制示例')
xlabel('X')
ylabel('Y')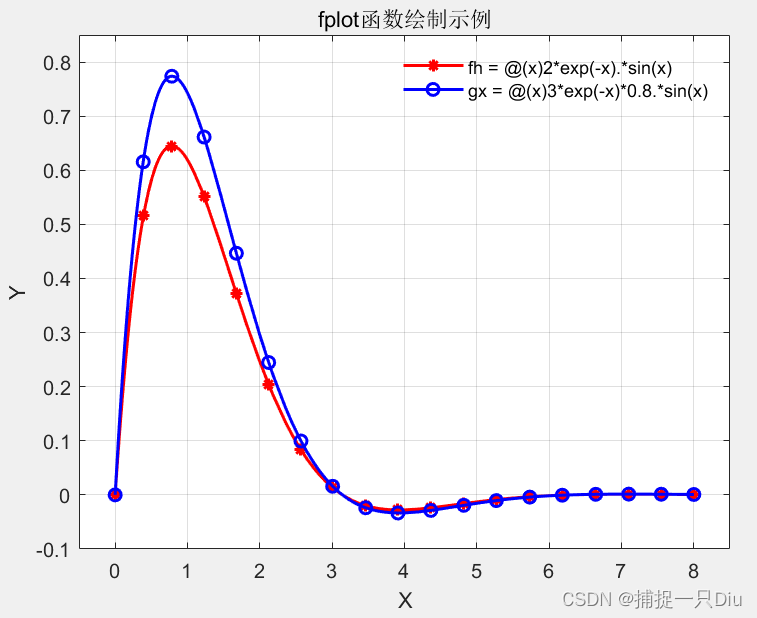

function y = eqsfun_fplot(x)
    y(:,1) = 200*sin(x)./x;
    y(:,2) = x.^2 - 3.5*x + 10;
end

clc,clear
fplot(@eqsfun_fplot,[-20,20],'LineWidth',1.5)
grid on
legend('y_1 = 200*sin(x)./x','y_2 = x.^2 - 3.5*x + 10')
legend('boxoff')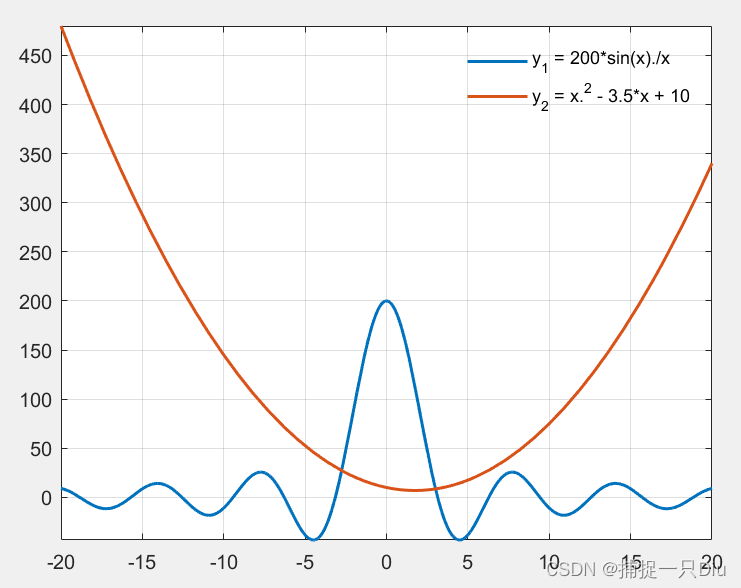

二、函数极值

一元函数极值

clc,clear
fh = @(x)x - 1./x + 5;
fplot(fh,[-10,10],'b-','LineWidth',1.5)
grid on
% fminbnd: Single-variable bounded nonlinear function minimization.
% exitflag > 0收敛到解，exitflag = 0已达最大迭代次数，exitflag < 0不收敛；
options = optimset('Display','iter','PlotFcns',@optimplotfval,'TolX',1e-6);
[x,fval,exitflag,output] = fminbnd(fh,-10,1,options)

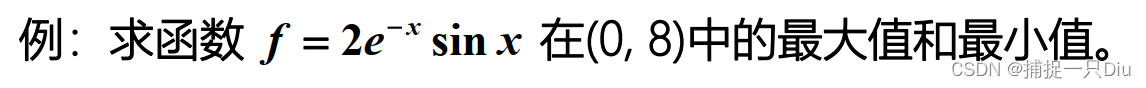
fh_min = @(x)2*exp(-x).*sin(x); %最小值匿名函数
fh_max = @(x)-2*exp(-x).*sin(x); %最大值匿名函数，前加负号
[xmin,fmin,exitflag] = fminbnd(fh_min,0,8);
[xmax,fmax,exitflag] = fminbnd(fh_max,0,8);
fplot(fh_min,[0,8])
axis([0 8 -0.1 0.7]) %改变坐标轴的范围
text(xmin+0.1,fmin,['最小值点：',num2str(fmin)])
text(xmax+0.1,-fmax,['最大值点：',num2str(-fmax)])
hold on
plot(xmin,fmin,'ro', xmax,-fmax, 'bo')
grid on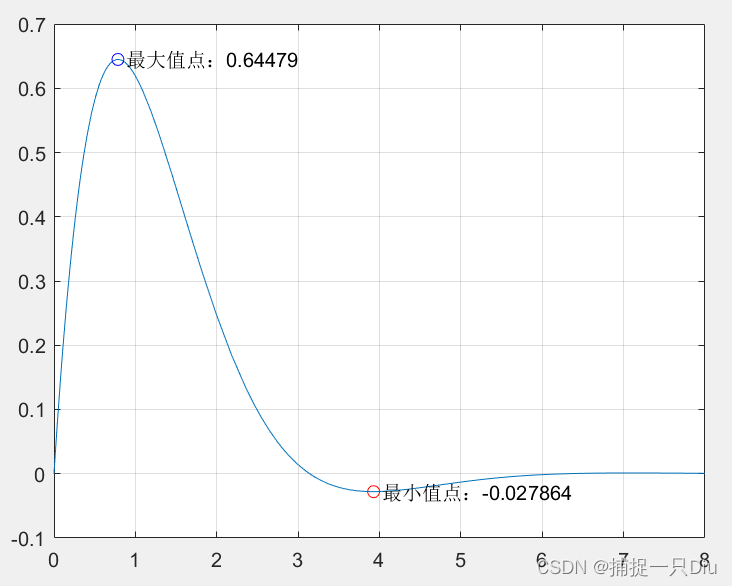

多元函数的极小值：

% [x,fval,exitflag,output] = fminsearch(@fh, x0, options)
% 此函数使用单纯型法搜索最值。其中𝒇𝒉为待求最值的向量函数，𝒙𝟎为搜索过程开始时自变量的初始值。
% [x,fval,exitflag,output,grad,hessian] = fminunc(@fh,x0 , options)
% 此函数使用牛顿法搜索最值，在效率上有所提高。

% fh = @(x,y)(x.^2-2*x).*exp(-x.^2-y.^2-x.*y);
% fsurf(fh,'ShowContours','on')
x = -5:0.2:5;
y = -5:0.2:5;
[X,Y] = meshgrid(x,y);
Z = (X.^2-2*X).*exp(-X.^2-Y.^2-X.*Y);
mesh(X,Y,Z)
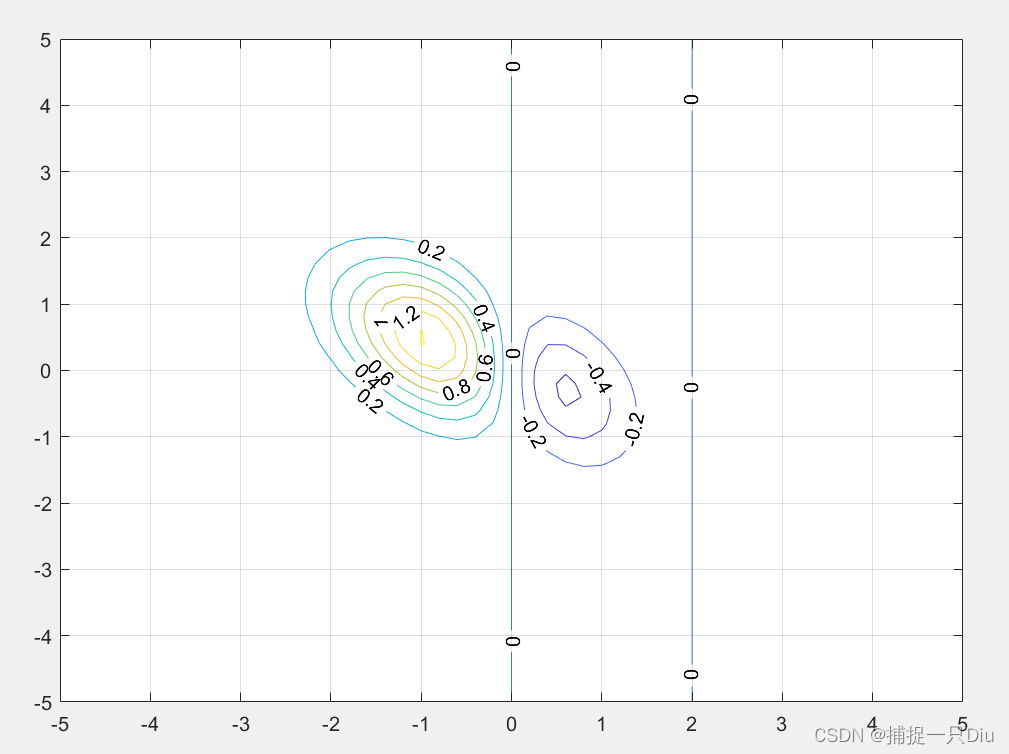
figure(2)
[c,h] = contour(X,Y,Z);
set(h,'ShowText','on')
grid on

fh = @(x)(x(1).^2-2*x(1)).*exp(-x(1).^2-x(2).^2-x(1).*x(2));
options = optimset('Display','iter','PlotFcns',@optimplotfval,'TolX',1e-6);
[x,fval,exitflag,output] = fminsearch(fh,[0.5,-0.5],options)
% [x,fval,exitflag,output] = fminunc(fh,[0.5,-0.5],options)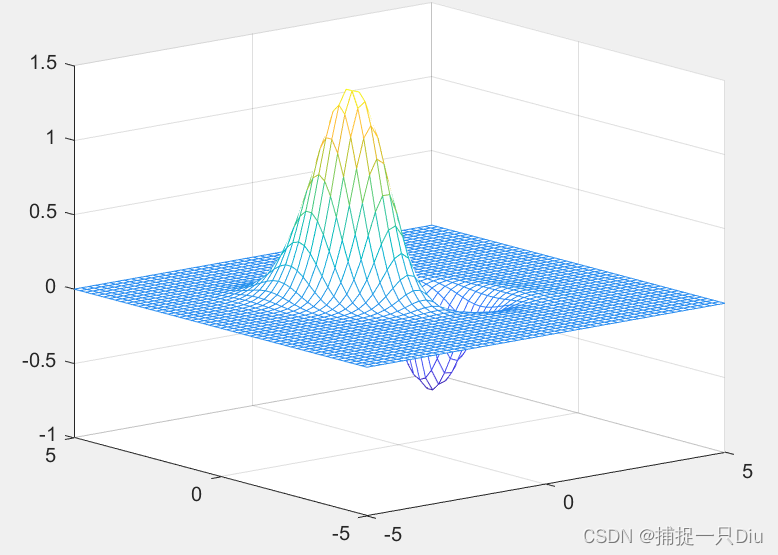

三、函数求解

单变量非线性函数求解：

clc,clear
fh = @(t)(sin(t)).^2.*exp(-0.1*t)-0.5*abs(t);
fplot(fh,[-5,5],'r-','LineWidth',1.5)
hold on 
grid on
fplot(@(t)0*t,[-5,5])
x0 = [-2,-0.5,0,0.5,1.6];  % 初值选择
sol = zeros(5,2);
for i = 1:5
    [t,y] = fzero(fh,x0(i));
    sol(i,1) = t;  % 零点
    sol(i,2) = y;  % 函数值
end
plot(sol(:,1),sol(:,2),'co','MarkerFaceColor','c')

[t1,y1,exitflag,output] = fzero(fh,-2)

多元非线性函数求解：

options = optimoptions('fsolve','Display','iter','PlotFcn',@optimplotfirstorderopt,'StepTolerance',1e-12);
[x,fval,exitflag,output] = fsolve(@nlineqs_fun,[0,0,0],options)

四、数值积分

矩形区域积分：

fh = @(x)sin(x);
format long
I1 = quad(fh,0,pi/2)
I2 = quadl(fh,0,pi/2)
I3 = quadgk(fh,0,pi/2)
I4 = integral(fh,0,pi/2)
% quad,quadl精度低，在未来的matlab中会被移除

fh = @(x)exp(-0.5*x).*sin(x+pi/6);
fplot(fh,[0,3*pi])
I = integral(fh,0,3*pi,'RelTol',1e-8,'AbsTol',1e-12)
x = 0:pi/30:3*pi;
y = fh(x);
h = area(x,y);
h.FaceColor = [0 0.75 0.75];
hold on; 
grid on
fplot(fh,[0,3*pi],'r-','LineWidth',1.5)
axis([-0.5,3*pi+0.5,-0.2,0.8])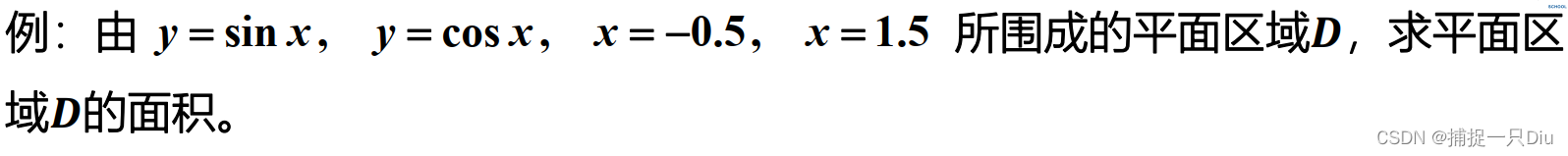

y1 = @(x)sin(x);
y2 = @(x)cos(x);
fplot(y1,[-1,2],'r-','LineWidth',1.5)
hold on
fplot(y2,[-1,2],'b-','LineWidth',1.5)
[x0,y0] = fzero(@(x)sin(x)-cos(x),[-0.5,1.5]);
x1 = -0.5:0.01:x0;
x2 = x0:0.01:1.5;
fill([x1,fliplr(x1)],[y1(x1),fliplr(y2(x1))],'c')
fill([x2,fliplr(x2)],[y2(x2),fliplr(y1(x2))],'c')

fh = @(x)abs(cos(x)-sin(x));
S = integral(fh,-0.5,1.5)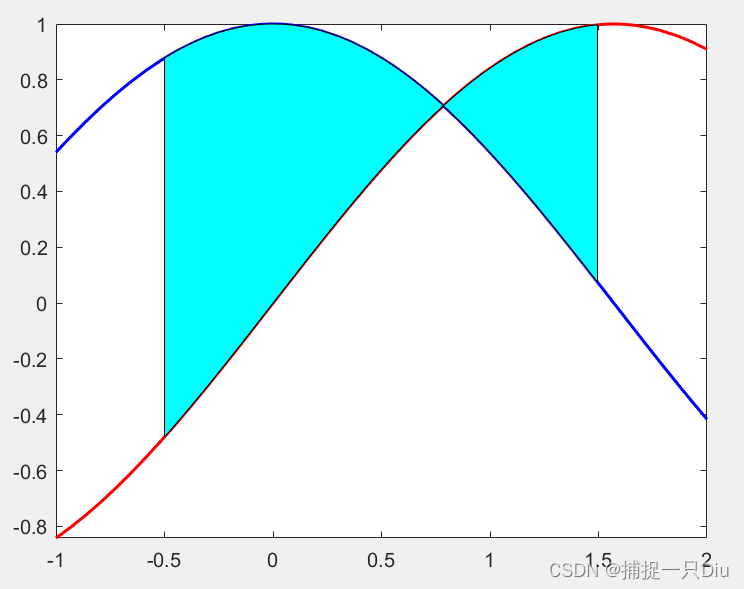

可以计算广义积分、含参积分问题、含奇点积分、高震荡积分、不连续积分、分段函数积分、围道积分...

fh = @(x)exp(x.^2).*(x<=2) + 80./(4-sin(16*pi*x)).*(x>2);
I1 = integral(fh,0,4,'Waypoints',[2])
I2 = quadgk(fh,0,4,'Waypoints',[2])

fh = @(x)exp(x).*log(x);
I = integral(fh,0,1)

fh = @(x)x.^5.*exp(-x).*sin(5*x);
fplot(fh,[0,100],'r-','LineWidth',1.5)
%积分限中可以有inf，但必须快速收敛
[q,errbnd] = quadgk(fh,0,inf,'RelTol',1e-8,'AbsTol',1e-12)
I = integral(fh,0,inf,'RelTol',1e-8,'AbsTol',1e-12)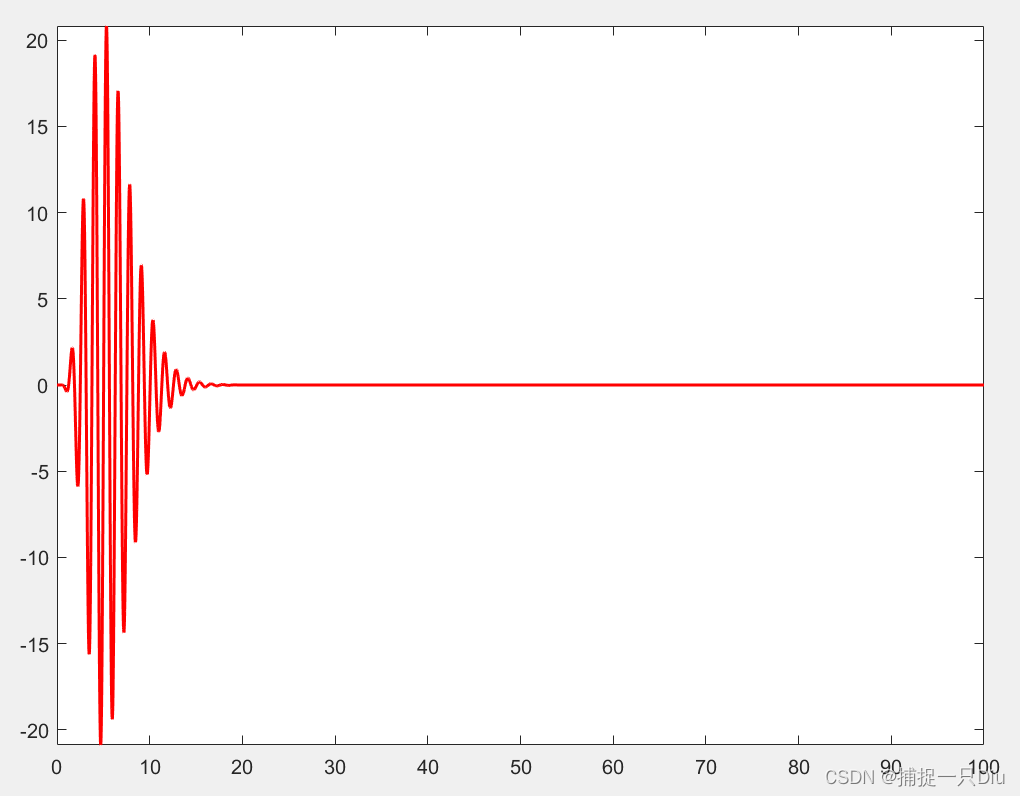

Waypoints = [-1-i 1-i 1+i -1+i -1-i];
plot(Waypoints);%绘制积分路径
xlabel('Real axis');
ylabel('Image axis');
axis([-1.5 1.5 -1.5 1.5]);
grid on;
%注意各点间使用直线连接
[Q,errbnd] = quadgk(@(z)1./(2*z - 1),-1-i,-1-i,'Waypoints',[1-i,1+i,-1+i])
[Q2,errbnd2] = quadgk(@(z)1./(2*z - 1),-1-i,-1-i,'Waypoints',Waypoints)
%使用这个的效果也是一样的，就是说始末点可以随便包不包含在Waypoints中
I = integral(@(z)1./(2*z - 1),-1-i,-1-i,'Waypoints',Waypoints)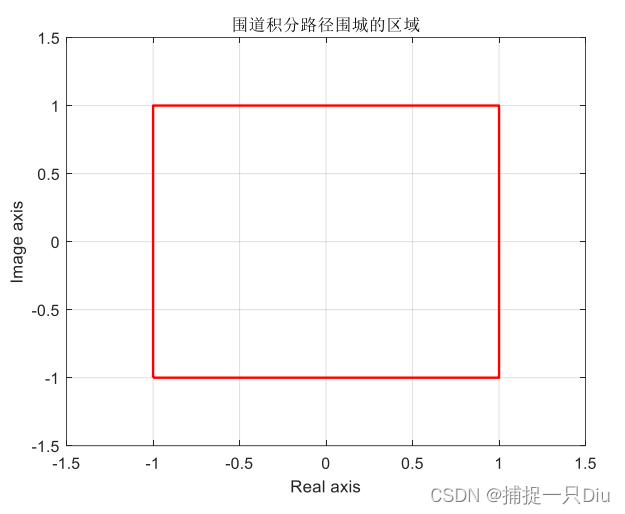

fh = @(x,alpha)exp(-alpha.*x.^2).*sin(alpha.^2.*x);
alphai = 0:0.1:4;  % 对alpha分点
I = integral(@(x)fh(x,alphai),0,inf,'RelTol',1e-8,'AbsTol',1e-12,'ArrayValued',true);
plot(alphai,I,'r-','LineWidth',1.5)
grid on
title('I(alpha)与alpha的关系曲线')
xlabel('alpha')
ylabel('I(alpha)')
grid on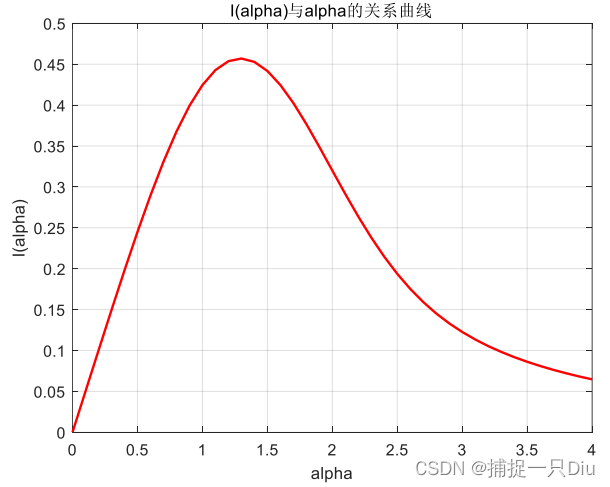

二重积分：

fh = @(x,y)exp(-x.^2/2).*sin(x.^2 + y);
I = integral2(fh,-2,2,-1,1,'RelTol',1e-10)

三重积分：

fh = @(x,y,z)4*x.*z.*exp(-x.^2.*y-z.^2);
I = integral3(fh,0,1,0,pi,0,pi,'AbsTol',1e-8,'RelTol',1e-12)

向量化积分：

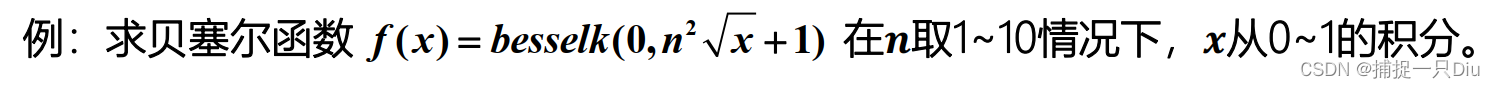
 fh2 = @(x)besselk(0,(1:10).^2*x.^0.5+1);
 I = integral(fh2,0,1,'ArrayValued',true)

离散数据积分：

trapezoid：通过梯形法计算近似积分

x = 0:pi/100:pi/2;
y = sin(x);
S1 = trapz(x,y)

x = -3:0.01:3; 
y = -5:0.01:5; 
[X,Y] = meshgrid(x,y); 
Z = X.^2 + Y.^2;
mesh(X,Y,Z)
%trapz 先对x求积分以生成列向量。然后，y上的积分可将列向量减少为单个标量。
%trapz 稍微高估计确切答案680，因为f(x,y)是凸函数。
V1 = trapz(y,trapz(x,Z,2)) 
V2 = trapz(x,trapz(y,Z,1))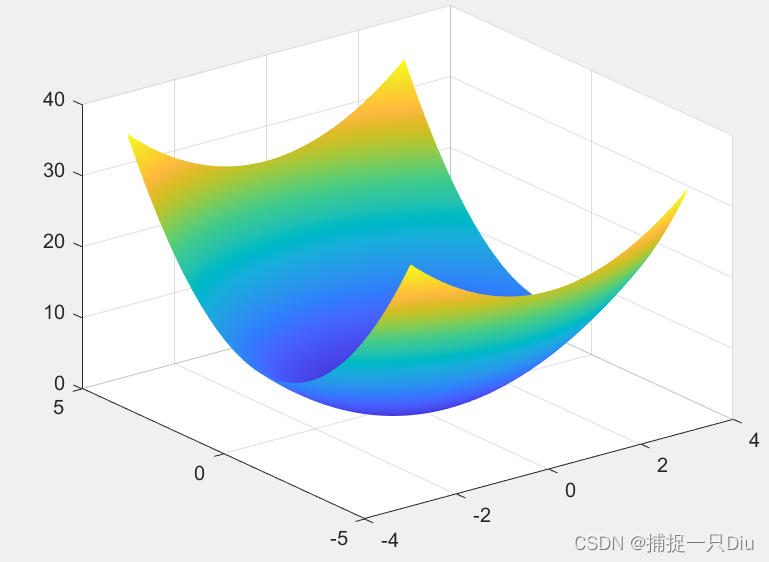

x = [0,2,4,5:9,10.5,11.5,12.5,14,16:24];
y = [20,25,30,35,40,50,155,92,60,62,60,43,59,140,120,68,60,80,55,65,20];
plot(x,y,'r-','LineWidth',1.5)
grid on
tf1 = trapz(x,y)
xi = 0:1/60:24;
yi = spline(x,y,xi);
hold on
plot(xi,yi,'b-','LineWidth',1.5)
tf2 = trapz(xi,yi)

pp = spline(x,y); %三次样条插值生成插值点系数矩阵
fh = @(x)fnval(pp,x); %获得系数矩阵函数
tf = integral(fh,0,24) %采用一重积分函数

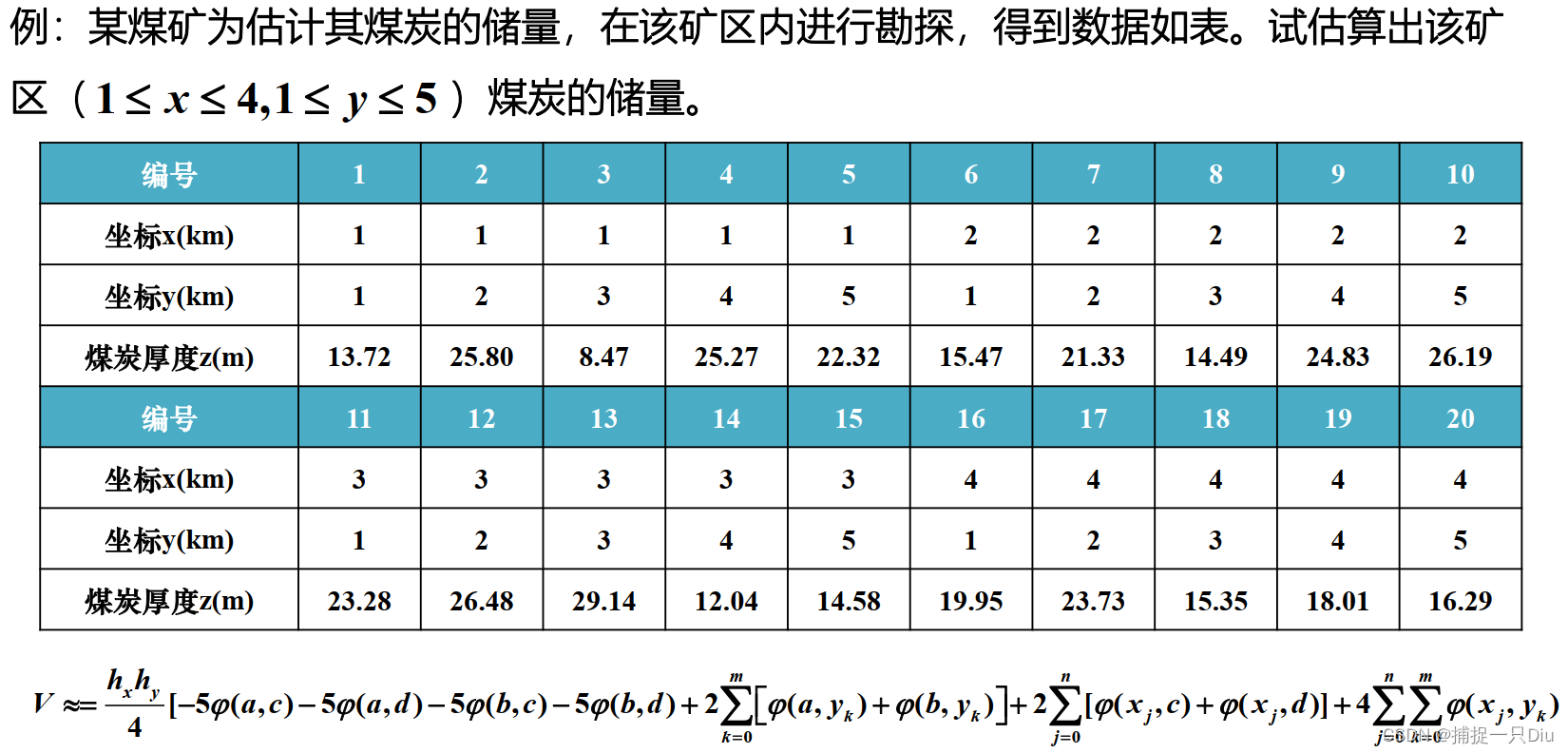
x = [1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 4 4 4 4 4]*1000;
y = [1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5]*1000;
z = -[13.72 25.80 8.47 25.27 22.32 15.47 21.33 14.49 24.83 26.19 23.28...
    26.48 29.14 12.04 14.58 19.95 23.73 15.35 18.01 16.29];
hx = 1000:10:4000;
hy = 1000:10:5000;
[X,Y] = meshgrid(hx,hy);
Z = griddata(x,y,z,X,Y,'cubic');
mesh(X,Y,Z)
V1 = trapz(hy,trapz(hx,Z,2))
n = length(hx);
m = length(hy);
V2 = -10*10*(-5*Z(1,1)-5*Z(1,n)-5*Z(m,1)-5*Z(m,n)+2*(sum(Z(1,:)+Z(m,:))+sum(Z(:,1)+Z(:,n)))+4*sum(sum(Z)))/4

一般区域的二重积分：

fh = @(x,y)sqrt(10000-x.^2);
tic,I1 = quad2d(fh,-100,100,@(x)-sqrt(10000-x.^2),@(x)sqrt(10000-x.^2)),toc
tic,I2 = integral2(fh,-100,100,@(x)-sqrt(10000-x.^2),@(x)sqrt(10000-x.^2)),toc % 一般效率更高

fh = @(x,y)exp(sin(x)).*log(y);
tic,I1 = quad2d(fh,10,20,@(x)5*x,@(x)x.^2),toc
tic,I2 = integral2(fh,10,20,@(x)5*x,@(x)x.^2),toc

一般区域的三重积分：

fh = @(x,y,z)x.*sin(y+z).*(x+z.^2);
xmin = 1;
xmax = 2;
ymin = @(x)sqrt(x); %y的下限
ymax = @(x)2*x; %y的上限
zmin = @(x,y)x.*y; %z的下限，是关于x和y的函数
zmax = @(x,y)2*x + y; %z的上限，是关于x和y的函数
q = integral3(fh,xmin,xmax,ymin,ymax,zmin,zmax)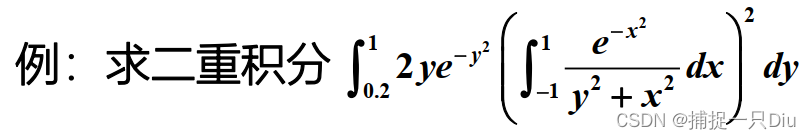

fhy = @(y)2*y.*exp(-y.^2).*(integral(@(x)exp(-x.^2)./(y.^2+x.^2),-1,1))^2;
I = integral(fhy,0.2,1,'ArrayValued',true)

基本的蒙特卡洛积分法（Monte Carlo）：

fhm = @(x)(x(:,1).^4 - 8*x(:,1).*x(:,2) + 2*sin(x(:,2)) - 3);
n = 1000000;
x(:,1) = unifrnd(2,5,n,1);
x(:,2) = unifrnd(0,23,n,1);
ind = (x(:,2) >= 0 & (x(:,2) <= x(:,1).^2 - 2));
% 期望法
fhIm = (5-2)*(23-0)*sum(fhm(x(ind,:)))/n

fh = @(x,y)(x.^4 - 8*x.*y + 2*sin(y) - 3);
fhI = integral2(fh,2,5,0,@(x)(x.^2-2),'RelTol',1e-10)

fh = @(x)(sqrt(x(:,1).*x(:,2)).*log(x(:,3)) + sin(x(:,4)./x(:,2)));
n = 1000000;
x(:,1) = unifrnd(1,2,1,n); %x1上下限
x(:,2) = unifrnd(1,6,1,n); %x2上下限
x(:,3) = unifrnd(1,24,1,n); %x3上下限
x(:,4) = unifrnd(2,98,1,n); %x4上下限
ind = (x(:,2) >= x(:,1) & x(:,2) <= 3*x(:,1)) &...
      (x(:,3) >= x(:,1).*x(:,2) & x(:,3) <= 2*x(:,1).*x(:,2)) &...
      (x(:,4) >= (x(:,1)+x(:,1).*x(:,3)) & x(:,4) <= (x(:,1)+2*x(:,1).*x(:,3)));
fnI = (2-1)*(6-1)*(24-1)*(98-2)*sum(fh(x(ind,:)))/n

等分布序列的蒙特卡洛积分法：

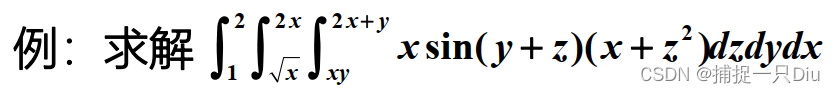
fh = @(x)x(:,1).*sin(x(:,2)+x(:,3)).*(x(:,1)+x(:,3).^2);
n = 100000000;
data = bsxfun(@times, repmat(1:n,3,1),[sqrt(2);sqrt(3);sqrt(6)/3]);
data = mod(data,1);  % 剩下小数部分
x(:,1) = data(1,:)+1;
x(:,2) = 3*data(2,:)+1;
x(:,3) = 7*data(3,:)+1;
ind = (x(:,2)>=sqrt(x(:,1)) & x(:,2)<=2*x(:,1) & x(:,3)>=x(:,1).*x(:,2) & x(:,3)<=2*x(:,1)+x(:,2));
In = (2-1)*(4-1)*(8-1)*sum(fh(x(ind,:)))/n