机器学习——编程实现从零构造训练集的决策树

news2025/10/31 17:11:10

自己搭建一棵决策树【长文预警】

忙了一个周末就写到了“构建决策树”这一步，还没有考虑划分测试集、验证集、“缺失值、连续值”，预剪枝、后剪枝的部分，后面再补吧（挖坑）

第二节内容：验证集划分\k折交叉检验 机器学习——编程从零实现决策树【二】-CSDN博客

目录

1、信息

1）基本算法过程

2）信息熵和信息增益的计算方式

2、做点假设，简化运算

3、拆解算法过程

0）结点类

1）同类样本判断

2）数据集能否再拆解

3）选取最优属性

步骤1

步骤2：

步骤3：

步骤4： 

 步骤5：

4）构造新结点

4、完整的结点类代码

5、完整的构造树的过程

6、建树

1）准备数据集

2）建树

7、绘图查看树的结构

1）绘图代码

2）结果

3）预测

完整的代码指路

DrawPixel/decisionTree.ipynb at main · ndsoi/DrawPixel (github.com)

1、信息

1）基本算法过程

2）信息熵和信息增益的计算方式

2、做点假设，简化运算

 ① 为了选择最优的属性进行划分，我们需要计算信息增益，而计算信息增益需要用到信息：

        1、选取的属性attr有多少种取值？

                (用西瓜分类的例子，考虑属性”纹理“，就有3种取值——”清晰“、”稍糊“和”模糊“）

        2、每种取值有哪些数据?这些数据中有多少是A类别的，又有多少是B类别的..？

                比如对原始数据集考虑”纹理=清晰“的数据，那么有7个是好瓜，有2个是坏瓜

② 计算完信息增益之后，我们选信息增益最大的属性，按照这个属性划分数据集，生成子结点

注意这里的划分数据集，事实上我们在完成①.2问题的时候就已经“划分了”一次数据集，只是我们没有记录下来，类似这样的“冗余”计算有很多，为了尽量减少“重复”计算，我重规划算法的步骤如下：

1、设总共有class_num个类别，假设我们初始化结点node的时候就知道了这个数据集的如下信息：

数据集        self.data

属性集        self.attr

该数据集内样本数量最多的类别        self.max

该数据集内每个类别的样本数量        self.cal_class 是一个列表，每一个元素是|Dv|

2、基于假设1： 

计算Ent(D)：

def Ent(D,cal_class):
  sum = len(D) # 样本总数
  # 求占比
  re = 0
  for k in cal_class:
    pk_class = k/sum
    if pk_class != 0:
      re -= pk_class* math.log(pk_class,2)
  return re

3、拆解算法过程

0）结点类

class Node():
  def __init__(self,D,A,max,cal_class,class_num):
    self.data = D
    self.attr = A
    self.class_num = class_num
    self.cal_class = cal_class

    self.max = max
    self.label = 0 # 0表示非叶结点 1表示叶结点
    self.Class = 0 # 默认一个
    self.flag = "init"

1）同类样本判断

若要判断D中的样本是否同属于一个类别：只需要判断self.max的数量是否等于class_num

  def isSameClass(self):
    if self.cal_class[self.max] == len(self.data):
      return True
    return False

2）数据集能否再拆解

若D中样本不属于同一类，那么接下来要看D中的样本是否还能再分解：

def isNoAttr(self):
    # 属性集为空
    if self.attr == None or self.attr==[]:
      return True,[]
    # 存储取值不同的属性
    self.Attr_Div = []
    for a in self.attr:
      a1 = self.data[0][a]
      for d in self.data:
        if d[a] != a1:
          self.Attr_Div.append(a)
          break
    # 无可分的属性
    if self.Attr_Div == []:
      return True,[]

    return False,self.Attr_Div

3）选取最优属性

从2）中获取了当前node数据集进一步可以分解的属性范围(self.Attr_Div),对于self.Attr_Div中的每一个attr，我们需要做的事情还有：

1. 找出属性attr的所有取值

2. 按照attr的不同取值将self.data划分成互斥的子集Dv_{attr=a1},Dv_{attr_{a_2}}...Dv_{a_n} 简称为Dv

3. 计算|Dv|和 Ent(Dv) 

4. 计算出attr的Gain

5. 重复步骤2-4 计算出所有attr的Gain， 选出Gain最大的attr

步骤1

# 属性attr的取值大全
def attrAllvalue(D,attr):
  Allvalue = {}
  for d in D:
    Allvalue[d[attr]] = 0
  return Allvalue

步骤2：

def divDataByattr(D,attr):
  # 建立一个字典，key是attr的取值，已初始化数值为0
  re = attrAllvalue(D,attr)
  n = len(re) # 要划分出n个子数据集
  SubDataSets = {}
  for key,value in re.items():
    SubDataSets[key] = []
  for d in D:
    SubDataSets[d[attr]].append(d)
  return SubDataSets

divDataByattr获得形如： {'清晰':[数据1,数据2],'模糊':[数据3],'稍糊':[数据4]} 的字典

步骤3：

为了计算Ent(Dv)我们需要获得Dv的cal_class，下列函数计算了数据集子集Dv的max和cal_class

# 获取maxnumClass
def calMaxClass(D,class_num):
  # 统计数据集D中各类样本的数目
  cal_class = [0 for i in range(class_num)]
  max = 0
  for d in D:
    cal_class[d['Class']]+=1
    if cal_class[d['Class']] > cal_class[max]:
      max = d['Class']
  return max,cal_class

步骤4： 

确定一个attr，划分出子集的集合,遍历子集集合，然后调用Ent函数，组合计算（加粗部分就是Gain函数所做的事情）

# 信息增益
def Gain(D,attr,class_info):
  max,cal_class = calMaxClass(D,class_num)
  EntD = Ent(D,cal_class)
  SubDataSets = divDataByattr(D,attr)
  EntDv = 0
  for value,Dv in SubDataSets.items():
    # cal_class
    max,cal_class=calMaxClass(Dv,class_num)
    class_info.append([max,cal_class])
    EntDv +=len(Dv)/len(D)*Ent(Dv,cal_class)
  Gain_D_attr = EntD-EntDv
  return Gain_D_attr

补充：这里的class_info就是记录下每一个Dv的max和cal_class，用于后续传参给node 初始化

 步骤5：

def choseAttr(D,attrSet):
  compar = 0

  Gain_D = {}
  for attr in attrSet:
    SubDataSets = divDataByattr(D,attr)
    EntDv = 0
    # 补充上Dv额外的参数
    class_info = []
    Gain_D_attr = Gain(D,attr,class_info)
    # 记录数据集D用属性attr做划分时所有的已知信息，包括gain，数据子集，数据子集的class_num和max类
    Gain_D[attr] = {'gain':Gain_D_attr,'Dv':SubDataSets,'Dv_info':class_info}

  # 找gain最高的attr
  target = attrSet[0]
  for attr in attrSet:
    if Gain_D[attr]['gain'] > compar:
      compar = Gain_D[attr]['gain']
      target = attr

  return target,Gain_D

4）构造新结点

在完成3）的步骤5后，应该为选定的attr划分的子集生成新结点，新结点

# 选取最优属性
  attr,info = node.bestAttr()
  # 获取划分好的数据集
  SubDataSets = info[attr]['Dv']
  SubInfo = info[attr]['Dv_info']


  # 生成子node
  Attr = copy.deepcopy(Attr_Div)
  Attr.remove(attr)
  st = 0
  for value,subds in SubDataSets.items():
    # 因为假设是离散属性，所以新的self.attr必然要去掉已经选出的attr
    subnodeAttr = copy.deepcopy(Attr)
    # 获取已经算好的Dv的max和cal_class
    submax = SubInfo[st][0]
    subcal_class = SubInfo[st][1]
    st+=1

    # 生成新结点
    subnode = Node(subds,subnodeAttr,submax,subcal_class,class_num)
    subnode.setflag(attr)
    # 新结点还要继续加入tree进行讨论
    tree.put(subnode)

    # 父结点记录子结点的指引
    node.addsubDs(subnode,value)

4、完整的结点类代码

# 说明：
# 设数据集是[{},{},{},...,{}]的格式
# {}的格式是{'attr1':'value1,'attr2':'value2',..,'label':'class'}
# label是结点node：表明其为叶节点还是非叶节点
# Class 是当node为叶结点时，该集合的类别
#
# 类别的数量
class_num = 2
class Node():
  def __init__(self,D,A,max,cal_class,class_num):
    self.data = D
    self.attr = A
    self.class_num = class_num
    self.cal_class = cal_class

    self.max = max
    self.label = 0 # 0表示非叶结点 1表示叶结点
    self.Class = 0 # 默认一个
    self.flag = "init"

  def isSameClass(self):
    if self.cal_class[self.max] == len(self.data):
      return True
    return False

  def isNoAttr(self):
    # 属性集为空
    if self.attr == None or self.attr==[]:
      return True,[]
    # 存储取值不同的属性
    self.Attr_Div = []
    for a in self.attr:
      a1 = self.data[0][a]
      for d in self.data:
        if d[a] != a1:
          self.Attr_Div.append(a)
          break
    # 无可分的属性
    if self.Attr_Div == []:
      return True,[]

    return False,self.Attr_Div



  # 计算选取最优划分属性
  def bestAttr(self):
    # 指向划分的子结点
    self.subDs = {}
    self.bestattr,self.Gain_D = choseAttr(self.data,self.Attr_Div)
    return self.bestattr,self.Gain_D

  def setflag(self,attr):
    self.flag = attr


  # 设置subDs
  def addsubDs(self,node,value):
    self.subDs[value] = node

5、完整的构造树的过程

import copy
import queue

def do_tree(tree):
  node = tree.get()
  print(node.data)

  # 判断D中的类别是不是都是一类
  re = node.isSameClass()

  if re:
    print("当前node都属于同一类别")
    # 如果D中的数据都属于同一个类别
    node.Class = node.max
    node.label = 1 # 标记为叶子结点
    return

  # D中的数据并不属于同一个类别
  # 判断属性是否可分
  boolre,Attr_Div = node.isNoAttr()
  print(f"Attr_Div={Attr_Div}")
  # D中的属性不可再分
  if boolre == True:
    print("当前类别属性不可再分")
    node.label = 1
    node.Class = node.max
    return

  # 选取最优属性
  attr,info = node.bestAttr()
  # 获取划分好的数据集
  SubDataSets = info[attr]['Dv']
  SubInfo = info[attr]['Dv_info']


  # 生成子node
  Attr = copy.deepcopy(Attr_Div)
  Attr.remove(attr)
  st = 0
  for value,subds in SubDataSets.items():
    # 因为假设是离散属性，所以新的self.attr必然要去掉已经选出的attr
    subnodeAttr = copy.deepcopy(Attr)
    # 获取已经算好的Dv的max和cal_class
    submax = SubInfo[st][0]
    subcal_class = SubInfo[st][1]
    st+=1

    # 生成新结点
    subnode = Node(subds,subnodeAttr,submax,subcal_class,class_num)
    subnode.setflag(attr)
    # 新结点还要继续加入tree进行讨论
    tree.put(subnode)

    # 父结点记录子结点的指引
    node.addsubDs(subnode,value)

def TreeGenerate(D,A):
  # 计算初始数据集的max和cal_class
  max,cal_class = calMaxClass(D,class_num)
  # 生成根结点
  node = Node(D,A,max,cal_class,class_num)

  tree = queue.Queue()
  tree.put(node)
  while tree.empty() == False:
    do_tree(tree)
  return node

6、建树

1）准备数据集


dataSet = [
        # 1
        ['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
        # 2
        ['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'],
        # 3
        ['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
        # 4
        ['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'],
        # 5
        ['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
        # 6
        ['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '好瓜'],
        # 7
        ['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘', '好瓜'],
        # 8
        ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑', '好瓜'],

        # ----------------------------------------------------
        # 9
        ['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜'],
        # 10
        ['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', '坏瓜'],
        # 11
        ['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑', '坏瓜'],
        # 12
        ['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', '坏瓜'],
        # 13
        ['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑', '坏瓜'],
        # 14
        ['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑', '坏瓜'],
        # 15
        ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '坏瓜'],
        # 16
        ['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑', '坏瓜'],
        # 17
        ['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜']
    ]
Attr = ['色泽', '根蒂', '敲击', '纹理', '脐部', '触感']

# 硬编码类别
class_dict = {'坏瓜':0,'好瓜':1}

# 将数据合并格式
D = []
for i in range(len(dataSet)):
  d = {}
  for j in range(len(Attr)):
    d[Attr[j]] = dataSet[i][j]
  d['Class'] = class_dict[dataSet[i][-1]]
  D.append(d)

print(D)

2）建树

root = TreeGenerate(D,Attr)

7、绘图查看树的结构

1）绘图代码

只是打印每层的结点，通过分支数目得知父子结点的关系

cur = root
# 表示区分的属性

q = queue.Queue()
q.put(cur)
while q.empty()==False:
  # 这层的宽度
  width = q.qsize()
  for i in range(width):
    # 用/**/包住一个node
    print(" /*",end="")
    cur = q.get()
    if cur.label == 1:
      # 叶子结点
      print(f"叶子：{cur.Class,cur.flag,cur.data[0][cur.flag]}",end="")
    else:
      l = len(cur.subDs)
      print(f"被分类依据：{cur.flag}",end="")
      if cur.flag != "init":
        print(f"值:{cur.data[0][cur.flag]}",end="  ")
      print(f",分支：{l}个",end="")

      for key,nod in cur.subDs.items():
        q.put(nod)

    print("*/ ",end="")
  print("")

2）结果

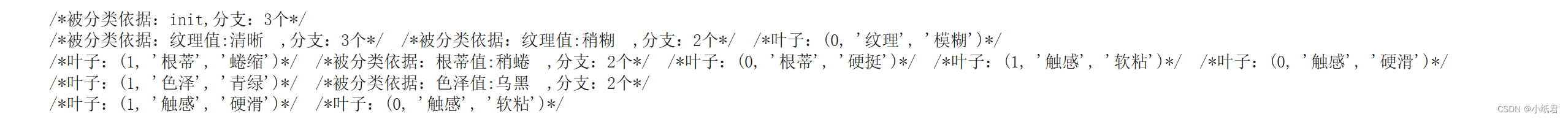
手绘还原：

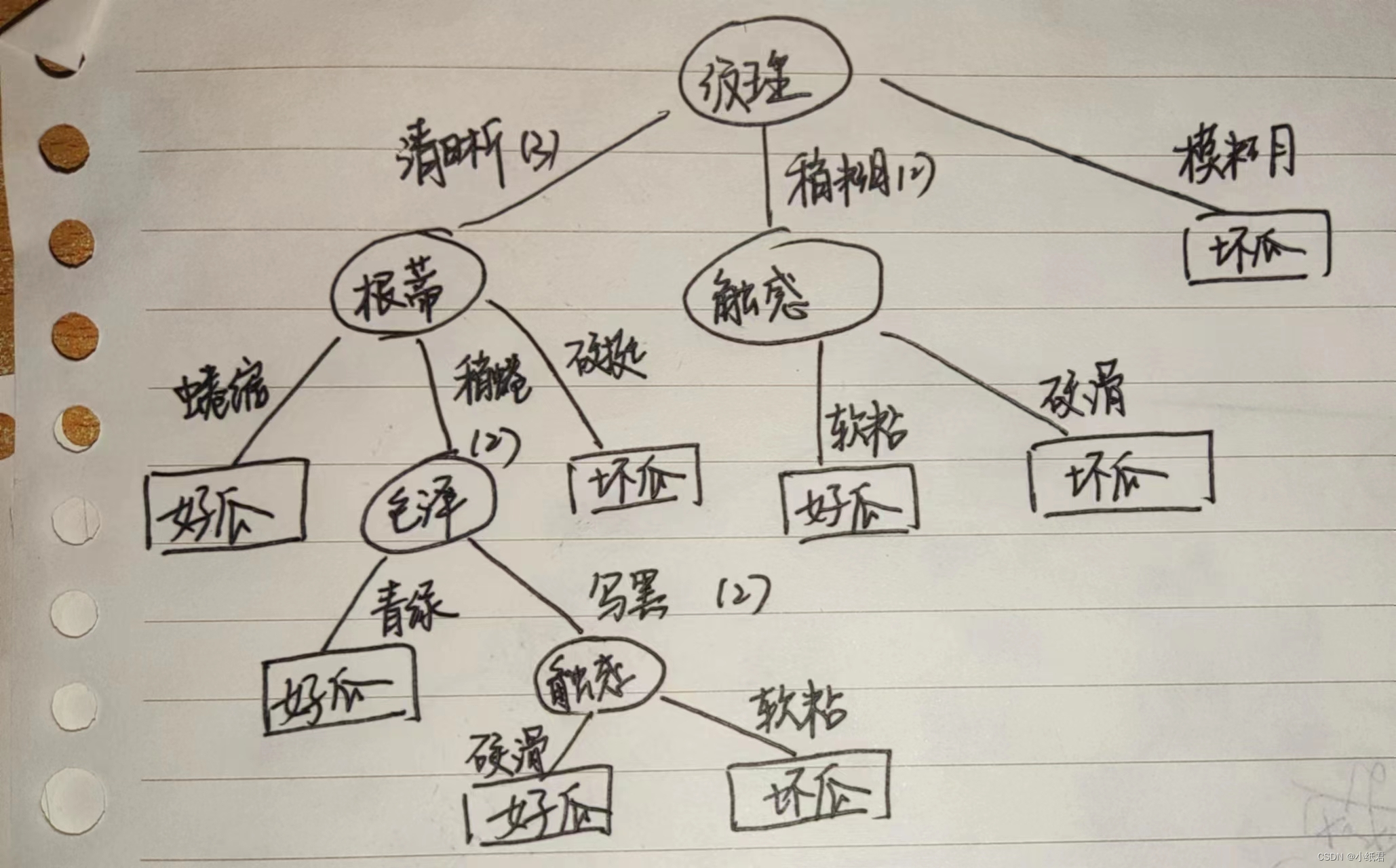
3）预测

投入一个样本，返回好瓜/坏瓜判断

def predict(data,root):
  cur = root
  while cur.label != 1:
    attr = cur.bestattr
    cur = cur.subDs[data[attr]]
  return cur.Class

for d in D:
  pd_label = predict(d,root)
  if pd_label == 0:
    print("坏瓜")
  else:
    print("好瓜")

结果打印8行好瓜，9行坏瓜

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1530403.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Docker-安装

Docker-安装

Docker ⛅Docker-安装🌠各平台支持情况🌠Server 版本安装☃️Ubuntu☃️Centos 🌠Docker 镜像源修改🌠Docker 目录修改 ⛅Docker-安装 🌠各平台支持情况 🌠Server 版本安装 ☃️Ubuntu 🍂安装…
阅读更多...
地脚螺栓的介绍

地脚螺栓的介绍

地脚螺栓简单来说，它是一种机械构件。通常用于铁路、公路、电力、桥梁、锅炉钢结构、塔吊、大型建筑等。一头预埋在地底下，另一头穿过设备用螺母拧紧，用来固定设备，钢结构设施，铁塔设施等，所以地脚螺栓拥有…
阅读更多...
上海亚商投顾：沪指震荡调整 北向资金全天净卖出超70亿

上海亚商投顾：沪指震荡调整 北向资金全天净卖出超70亿

上海亚商投顾前言：无惧大盘涨跌，解密龙虎榜资金，跟踪一线游资和机构资金动向，识别短期热点和强势个股。 一.市场情绪 沪指昨日震荡调整，创业板指尾盘跌超1%。猪肉股集体反弹，播恩集团、湘佳股份、傲农生物…
阅读更多...
vue项目：使用xlsx导出Excel数据

vue项目：使用xlsx导出Excel数据

文章目录 一、安装xlsx二、报错及解决三、编写公共方法四、方法使用 一、安装xlsx 执行命令：npm i xlsx file-saver --save 二、报错及解决 使用时：import XLSX from "xlsx"; 发现如下报错信息 报错原因：xlsx版本不兼容。 解…
阅读更多...
幼犬狗粮和成年犬狗粮该怎么挑选？

幼犬狗粮和成年犬狗粮该怎么挑选？

亲爱的狗友们，我们都知道，给狗狗选择适合的狗粮是非常重要的。那么，面对市面上琳琅满目的幼犬狗粮和成年犬狗粮，我们该如何挑选呢？别担心，接下来就让我来给大家支支招。 🐶 幼犬狗粮挑选篇 &…
阅读更多...
Linux 网络接口管理

Linux 网络接口管理

为了更深入的了解linux系统，为此做出网络接口管理的知识总结。看起来麻烦，其实一点都不难，相信多看多了解总会是没错的！❤️❤️ 一起加油吧！✨✨🎉🎉 文章目录 前言一、网络配置的文件介绍二、…
阅读更多...
路由器怎么做端口映射

路由器怎么做端口映射

路由器在网络中起到了连接不同设备和提供网络服务的重要作用。端口映射是一项常见的操作，它允许外部网络中的设备通过路由器访问内部网络中的设备。我们将介绍如何在路由器上进行端口映射的设置。 理解端口映射 在开始操作之前，我们需要了解一些基本概念…
阅读更多...
JJJ：改善ubuntu网速慢的方法

JJJ：改善ubuntu网速慢的方法

Ubuntu 系统默认的软件下载源由于服务器的原因， 在国内的下载速度往往比较慢，这时我 们可以将 Ubuntu 系统的软件下载源更改为国内软件源，譬如阿里源、中科大源、清华源等等， 下载速度相比 Ubuntu 官方软件源会快很多！…
阅读更多...
机器学习 - 训练模型

机器学习 - 训练模型

接着这一篇博客做进一步说明： 机器学习 - 选择模型 为了解决测试和预测之间的差距，可以通过更新 internal parameters, the weights set randomly use nn.Parameter() and bias set randomly use torch.randn(). Much of the time you won’t know what…
阅读更多...
Python内置对象

Python内置对象

Python是一种强大的、动态类型的高级编程语言，其内置对象是构成程序的基础元素。Python的内置对象包括数字、字符串、列表、元组、字典、集合、布尔值和None等，每种对象都有特定的类型和用途。 01 什么是内置对象 这些对象是编程语言的基础构建块&…
阅读更多...
C语言 指针练习

C语言 指针练习

一、 a、b是两个浮点型变量&#xff0c;给a、b赋值&#xff0c;建立两个指针分别指向a的地址和b的地址&#xff0c;输出两个指针的值。 #include<stdio.h> int main() {float a,b,*p1,*p2;a10.2;b2.3;p1&a;p2&b;printf("a%f,b%f\n",a,b);printf("…
阅读更多...
软考高级：类的分类（边界类、控制类、实体类）概念和例题

软考高级：类的分类（边界类、控制类、实体类）概念和例题

作者&#xff1a;明明如月学长&#xff0c; CSDN 博客专家&#xff0c;大厂高级 Java 工程师&#xff0c;《性能优化方法论》作者、《解锁大厂思维&#xff1a;剖析《阿里巴巴Java开发手册》》、《再学经典&#xff1a;《Effective Java》独家解析》专栏作者。 热门文章推荐&am…
阅读更多...
【Java初阶（二）】分支与循环

【Java初阶（二）】分支与循环

❣博主主页: 33的博客❣ ▶文章专栏分类: Java从入门到精通◀ &#x1f69a;我的代码仓库: 33的代码仓库&#x1f69a; 目录 1.前言2.顺序结构3.分支循环3.1if语句3.2switch语句 4.循环结构4.1while循环4.2 break和continue4.3 for循环4.4 do while循环 5.输入输出5.1输出5.2输…
阅读更多...
记录C++中，子类同名属性并不能完全覆盖父类属性的问题

记录C++中，子类同名属性并不能完全覆盖父类属性的问题

问题代码&#xff1a; 首先看一段代码&#xff1a;很简单&#xff0c;就是BBB继承自AAA&#xff0c;然后BBB重写定义了同名属性&#xff0c;然后调用父类AAA的打印函数&#xff1a; #include <iostream> using namespace std;class AAA { public:AAA() {}~AAA() {}void …
阅读更多...
Django单表数据库操作

Django单表数据库操作

单表操作 测试脚本 当你只想测试django某一个py文件的内容,可以不用书写前后端的交互,直接写一个测试脚本即可 单表删除 数据库操作方法: 1.all():查询所有的数据 2.filter():带有过滤条件的查询 3.get():直接拿数据对象,不存在则报错 4.first():拿queryset里面的第一个元素…
阅读更多...
【数据结构取经之路】栈

【数据结构取经之路】栈

目录 引言 栈的性质 顺序栈 栈的基本操作 初始化 销毁 插入 删除 判空 取栈顶元素 栈的大小 完整代码&#xff1a; 引言 栈(stack)&#xff0c;可以用数组实现&#xff0c;也可以用链表实现。用数组实现的栈叫顺序栈&#xff0c;用链表实现的栈叫链式栈&#…
阅读更多...
红外相机和RGB相机标定：实现两种模态数据融合

红外相机和RGB相机标定：实现两种模态数据融合

1. 前期准备 RGB相机&#xff1a;森云智能SG2-IMX390&#xff0c;1个红外相机&#xff1a;艾睿光电IR-Pilot 640X-32G&#xff0c;1个红外标定板&#xff1a;https://item.taobao.com/item.htm?_ujp3fdd12b99&id644506141871&spma1z09.2.0.0.5f822e8dKrxxYI 2.操作步…
阅读更多...
C# 方法（函数）

C# 方法（函数）

文章目录 C# 方法&#xff08;函数&#xff09;简单示例程序代码运行效果 值传递和引用传递示例程序 运行效果按输出传递参数运行结果 C# 方法&#xff08;函数&#xff09; 简单示例 程序代码 访问的限制符 using System; using System.Collections.Generic; using Syste…
阅读更多...
DevEco Studio 项目创建

DevEco Studio 项目创建

安装DevEco Studio后开始使用&#xff0c;双击桌面DevEco Studio 快捷方式弹出界面&#xff1a; 选择Application —> Empty Ability&#xff0c;点击Next 项目配置 Project name&#xff1a;工程的名称&#xff0c;可以自定义&#xff0c;由大小写字母、数字和下划线组成。…
阅读更多...
JavaSE——面向对象高级二（3/4）-接口（认识接口、接口的好处）以及接口的综合案例（设计班级学生的信息管理模块）

JavaSE——面向对象高级二（3/4）-接口（认识接口、接口的好处）以及接口的综合案例（设计班级学生的信息管理模块）

目录 接口 认识接口 接口的好处 接口的综合案例 需求 学生类 班级管理类 学生操作接口 学生操作类 完善班级管理类 测试 接口 认识接口 Java提供了一个关键字 interface&#xff0c;用这个关键字我们可以定义出一个特殊的结构&#xff1a;接口。 public interface…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023