题目描述
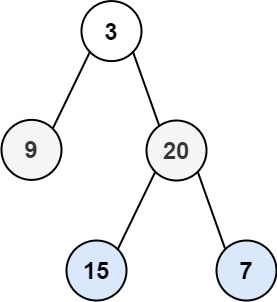
如图所示的螺旋折线经过平面上所有整点恰好一次。
对于整点(X, Y),我们定义它到原点的距离dis(X, Y)是从原点到(X, Y)的螺旋折线段的长度。
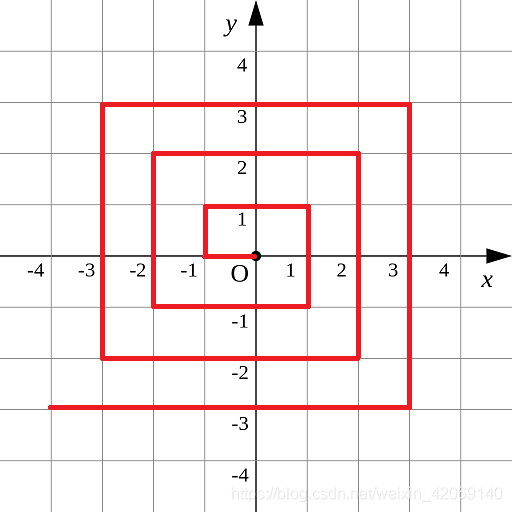
例如dis(0, 1)=3, dis(-2, -1)=9
给出整点坐标(X, Y),你能计算出dis(X, Y)吗?
【输入格式】
X和Y
对于40%的数据,-1000 <= X, Y <= 1000
对于70%的数据,-100000 <= X, Y <= 100000
对于100%的数据, -1000000000 <= X, Y <= 1000000000
【输出格式】
输出dis(X, Y)
【输入样例】
0 1
【输出样例】
3
代码
import java.util.Scanner;
/**
* * @author Fancier
* @version 1.0
* @description: 螺旋折线
* @date 2024/3/13
*/
//-1000000000 <= X, Y <= 1000000000
public class Main {
public static void main(String[] args) {
Scanner cin = new Scanner(System.in);
long x = cin.nextInt(), y = cin.nextInt(), result;
//确定第几圈了
long rings = Math.max(Math.abs(x), Math.abs(y));
long inner = rings * (rings - 1) * 4;
long len = rings * 2;
//确定象限
if (x < 0 && y < 0 && x != y) {
if (x == -rings) {
//第一段
result = y + rings;
} else {
//第八段
result = rings - x + 3 * len;
}
} else if (x < 0 && y >= 0) {
if (x == -rings){
//第二段
result = y + rings;
} else {
//第三段
result = x + rings + len;
}
} else if (x >= 0 && y > 0) {
if (y == rings) {
//第四段
result = x + rings + len;
} else {
//第五段
result = rings - y + 2 * len;
}
} else {
if (x == rings) {
//第六段
result = rings - y + 2 * len;
} else {
//第七段
result = rings - x + 3 * len;
}
}
System.out.println(result + inner);
}
}
题解
分为4个象限, 每个象限分为两种情况
- y的绝对值大
- x的绝对值大
为了方便区分我们将其分为8段, 从第3象限顺时针开始
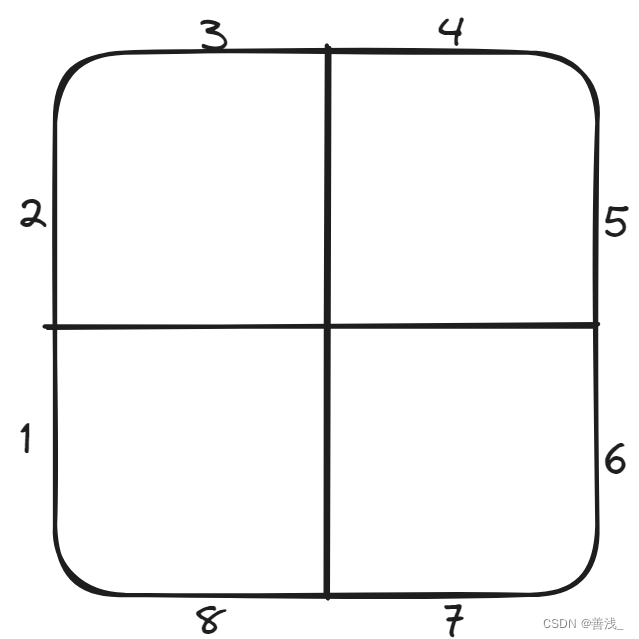
怎么区分第几圈
根据最大坐标的值
怎么计算一个完整的全的周长
i是圈数
周长 = 8 * i
第1圈的周长:8
第2圈的周长:16
怎么计算每段的长度
i为第几圈
第1,2段 : y + i
第3,4段: x + i
第5,6段: i - y;
第7,8段: i - x;
具体步骤:
先确定象限
再确定第几段
再计算
具体代码参上
好的!本次分享到这就结束了
如果对铁汁你有帮助的话,记得点赞👍+收藏⭐️+关注➕
我在这先行拜谢了:)






![[蓝桥杯 2020 省 AB3] 限高杆](https://img-blog.csdnimg.cn/direct/2ae712876b444a97a66fb8f9276fdd87.png)