对于强森算法的算法思想，如果给定的图中是没有负数的边，那么就可以使用迪杰斯特拉算法来进行遍历每个节点，找到它与其他节点的最短路径，而如果给定的图中是存在负数的边，但是不存在负数的环的时候，那么就可以使用算法对边长做一些修改并且可以准确的找到给定的两个节点之间的最短路径。

而对边长进行修改的时候，要注意两点，第一点是在修改之前，如果p是节点u，v之间的最短路径，那么在修改之后要必须保证p依然是节点u，v之间的最短路径，第二点就是要确保修改之后是不存在负数的边的。

针对以上两点，假设有一个函数T，它能给每个节点赋值，也就是吧节点vi作为参数传入函数T中，就可以得到一个数值T(vi)，如果用E（u，v）来表示图中每一条边（u，v）的长度，那么就可以修改为：

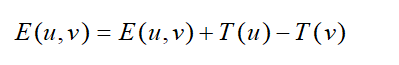
添加图片注释，不超过 140 字（可选）

在这样的修改之后，最短路径是不会发生变化的，而且假设P:{v0...vn}是起始节点v0抵达终节点vn的一条路径，当边长单招上面的公式进行修改之后，路径p的长度就变成：