最长公共子序列(二)

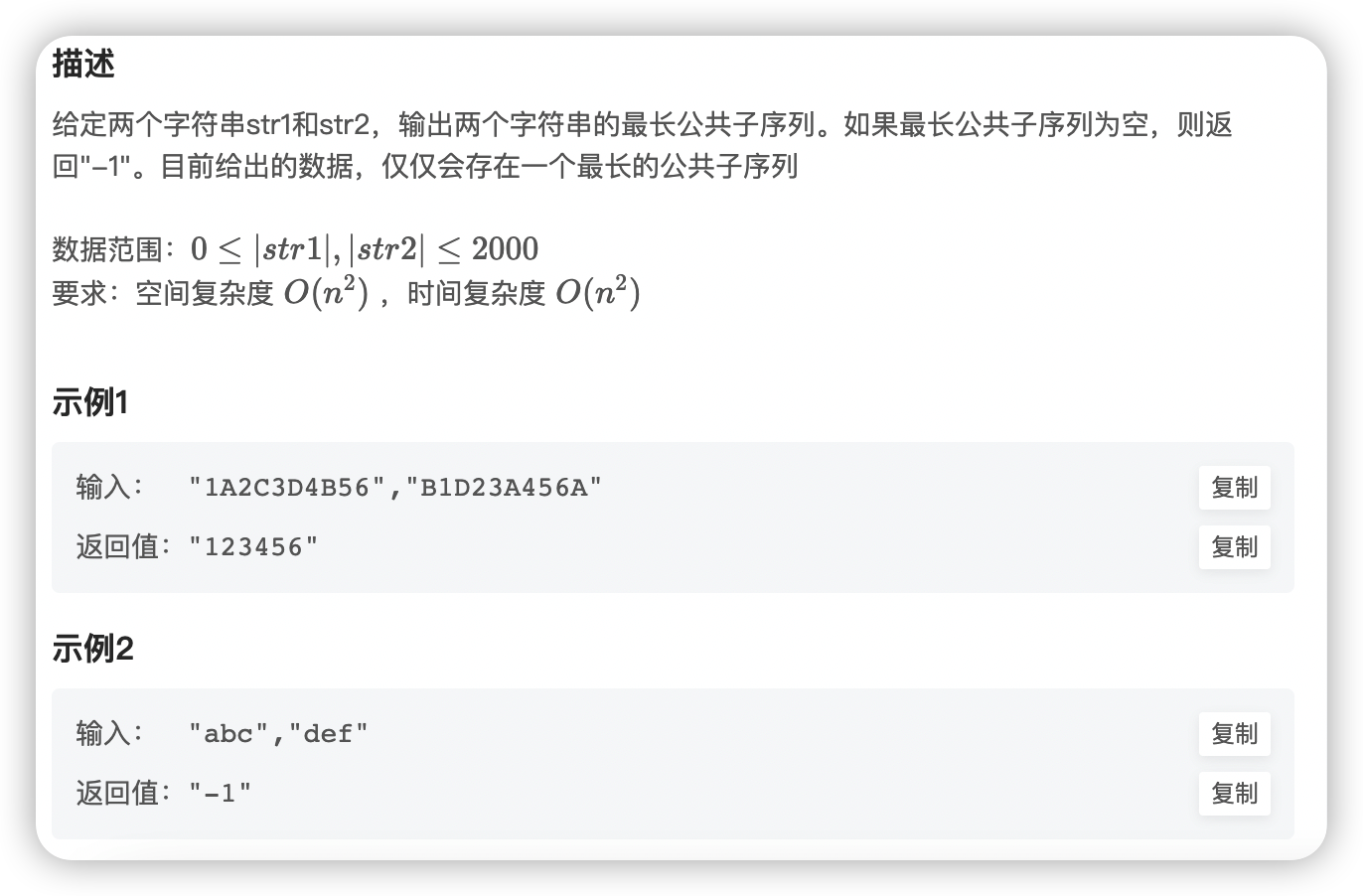
分析：
典型的动态规划，直接看代码了。

代码：

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * longest common subsequence
     * @param s1 string字符串 the string
     * @param s2 string字符串 the string
     * @return string字符串
     */
    public String LCS (String s1, String s2) {
        // write code here
        int m = s1.length();
        int n = s2.length();

        int[][] dp = new int[m+1][n+1];

        // dp[i][j] 含义：以i和j结尾的字符串的最长公共子序列长度
        // 转移方程：

        // 先找到最长子序列
        for(int i = 1;i<=m;i++) {
            for(int j = 1;j<=n;j++) {
                if(s1.charAt(i-1) == s2.charAt(j-1)) {
                    dp[i][j] = dp[i-1][j-1]+1;
                } else {
                    dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
                }
            }
        }

        // 倒推子序列
        int i = m;
        int j = n;
        StringBuilder sb = new StringBuilder();
        while(i>0&&j>0) {
            if(s1.charAt(i-1) == s2.charAt(j-1)) {
                sb.append(s1.charAt(i-1));
                i--;
                j--;
            } else {
                if(dp[i][j-1] > dp[i-1][j]) {
                    j--;
                } else if(dp[i][j-1] < dp[i-1][j]) {
                    i--;
                } else if(dp[i][j-1] == dp[i-1][j]) {
                    j--;
                }
            }
        }

        return sb.length() == 0 ? "-1" : sb.reverse().toString();
    }
}