当我们创建神经网络时，我们必须为初始权重和偏置做出选择。到目前为止，我们一直根据我在第一章中简要讨论过的一种方法来选择它们。提醒一下，那种方法是使用独立的高斯随机变量来选择权重和偏置，使它们的均值为0，标准差为1。虽然这种方法效果不错，但它相当随意，值得重新审视，看看我们是否能找到一种更好的方法来设置我们的初始权重和偏置，或许可以帮助我们的神经网络学习得更快。

事实证明，我们可以比使用归一化高斯更好地初始化。为了理解其中的原因，假设我们正在处理一个具有大量输入神经元 - 比如1000个 - 的网络。假设我们已经使用归一化高斯来初始化连接到第一个隐藏层的权重。现在我将专注于连接输入神经元和第一个隐藏层中的第一个神经元的权重，并忽略网络的其余部分。

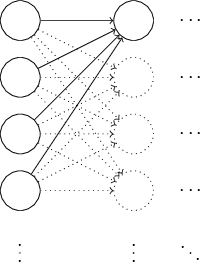
为简单起见，假设我们试图使用一个训练输入 x，在这个输入中，一半的输入神经元是开启的，即设置为 1，另一半的输入神经元是关闭的，即设置为 0。后续的论证更一般地适用，但从这个特殊情况你也可以理解主要观点。让我们考虑我们隐藏神经元的加权和 $z={\sum }_j{w}_j{x}_j+b$。这个总和中有 500 个项会消失，因为相应的输入 $x_j$ 为零。因此，z 是一个总共由 501 个归一化高斯随机变量构成的和，其中包括 500 个权重项和 1 个额外的偏置项。因此，z 本身服从均值为零、标准差为 $\sqrt{501}\approx 22.4$ 的高斯分布，。也就是说，z 有一个非常宽的高斯分布，完全不是尖峰的。

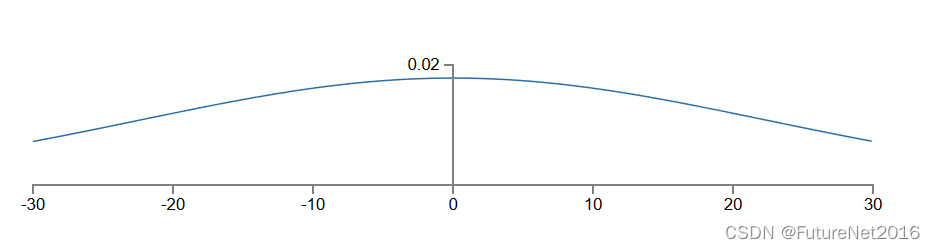
特别是，我们可以从这张图中看出，|z| 很可能会非常大，即 z≫1 或 z≪−1。如果是这种情况，那么隐藏神经元的输出 σ(z) 将非常接近于 1 或 0。这意味着我们的隐藏神经元将饱和。而我们知道，当这种情况发生时，对权重进行微小的更改将只会导致隐藏神经元的激活产生极小的变化。这种微小变化的隐藏神经元激活，反过来几乎不会对网络中的其他神经元产生影响，我们将看到成比例地微小的成本函数变化。因此，当我们使用梯度下降算法时，这些权重将学习得非常缓慢。这与我们在本章早些时候讨论的问题类似，在该问题中，饱和在错误值上的输出神经元导致学习变慢。我们通过巧妙选择成本函数解决了早期的问题。不幸的是，虽然这对饱和的输出神经元有所帮助，但对于饱和的隐藏神经元的问题却毫无作用。

我一直在谈论输入到第一个隐藏层的权重。当然，类似的论点也适用于后续的隐藏层：如果后续隐藏层的权重使用标准化的高斯分布进行初始化，那么激活往往会非常接近于 0 或 1，学习将会进行得非常缓慢。

有没有办法我们可以选择更好的权重和偏差初始化，以避免这种饱和，从而避免学习速度变慢？假设我们有一个具有 $n_{in}$ 个输入权重的神经元。那么我们将使用均值为 0，标准差为 $1/\sqrt{n_{\mathrm{in}}}$的高斯随机变量来初始化这些权重。也就是说，我们将缩小高斯分布，减少我们的神经元饱和的可能性。我们将继续选择偏差为均值为 0，标准差为 1 的高斯分布初始化偏置，稍后我将再谈到原因。通过这些选择，加权和 $z={\sum }_j{w}_j{x}_j+b$ 仍然是均值为 0 的高斯随机变量，但它的峰值要比以前明显得多。假设，正如我们之前所做的那样，500 个输入为零，500 个输入为 1。那么很容易证明，z 具有均值为 0 和标准差为 $\sqrt{3/2}=1.22\dots$ 的高斯分布。这比以前更尖峰，以至于即使与先前的图形相比，下面的图形也无法完全反映情况，因为我不得不重新调整了垂直轴的比例：
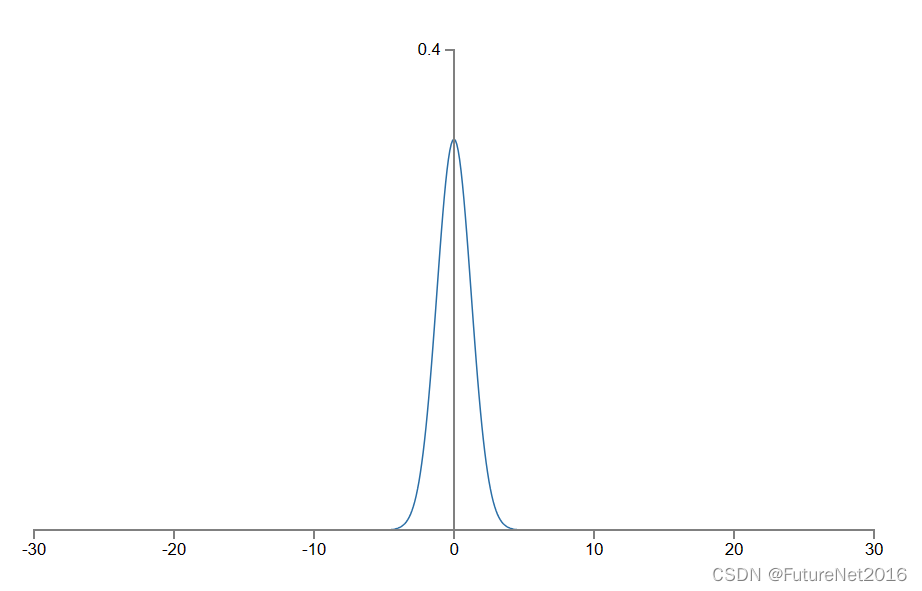这样的神经元饱和的可能性要小得多，因此出现学习减速的问题也相应减少了。

如上所述，我们将继续像以前那样初始化偏置，即使用均值为 0、标准差为 1 的高斯随机变量。这是可以接受的，因为这样做不会使神经元过度饱和的可能性增加太多。事实上，初始化偏差的方式并不重要，只要我们避免了饱和的问题。有些人甚至将所有偏差都初始化为 0，并依靠梯度下降来学习适当的偏差。但由于初始化偏置很可能不会产生太大的影响，因此我们将继续使用与以前相同的初始化过程。

让我们比较一下使用旧方法和新方法初始化权重的结果，在 MNIST 数字分类任务中进行比较。与以前一样，我们将使用 30 个隐藏神经元、迷你批量大小为 10、正则化参数 λ=5.0 和交叉熵成本函数。我们将把学习率略微从 η=0.5 降低到 0.1，因为这样可以使结果在图表中更容易看到。我们可以使用旧的权重初始化方法进行训练：

>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
>>> import network2
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0,
... evaluation_data=validation_data, 
... monitor_evaluation_accuracy=True)

我们也可以使用新的权重初始化方法进行训练。实际上，这甚至更容易，因为 network2 默认的权重初始化方式就是使用这种新方法。这意味着我们可以省略上面的 net.large_weight_initializer() 调用：

>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0,
... evaluation_data=validation_data, 
... monitor_evaluation_accuracy=True)

绘制结果如下：

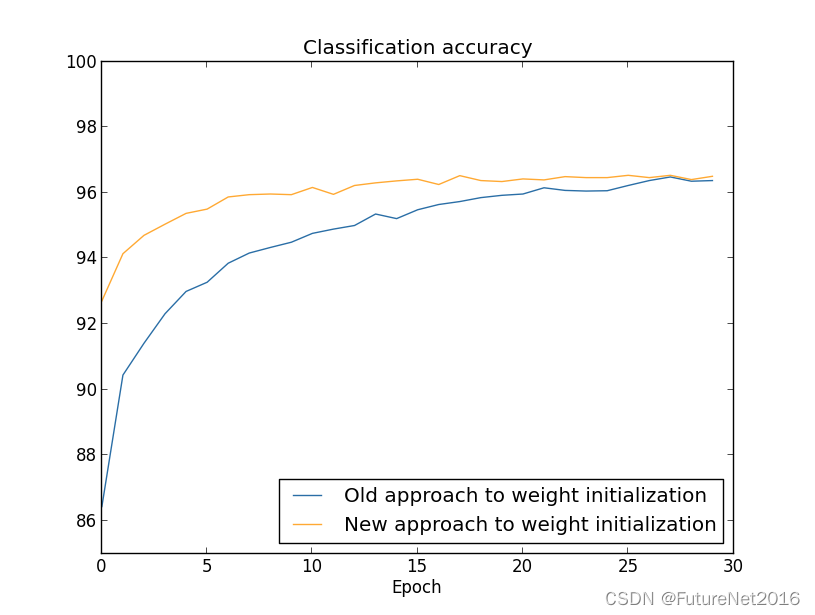
在这两种情况下，我们最终的分类准确率都略高于96%。两种情况下的最终分类准确率几乎完全相同。但是新的初始化技术使我们能够更快地达到这一水平。在训练的第一个周期结束时，旧的权重初始化方法的分类准确率不到87％，而新方法几乎达到了93％。看起来发生的事情是，我们的新的权重初始化方法让我们从一个更好的起点开始，这让我们能够更快地取得良好的结果。如果我们使用100个隐藏神经元绘制结果，也会看到相同的现象：

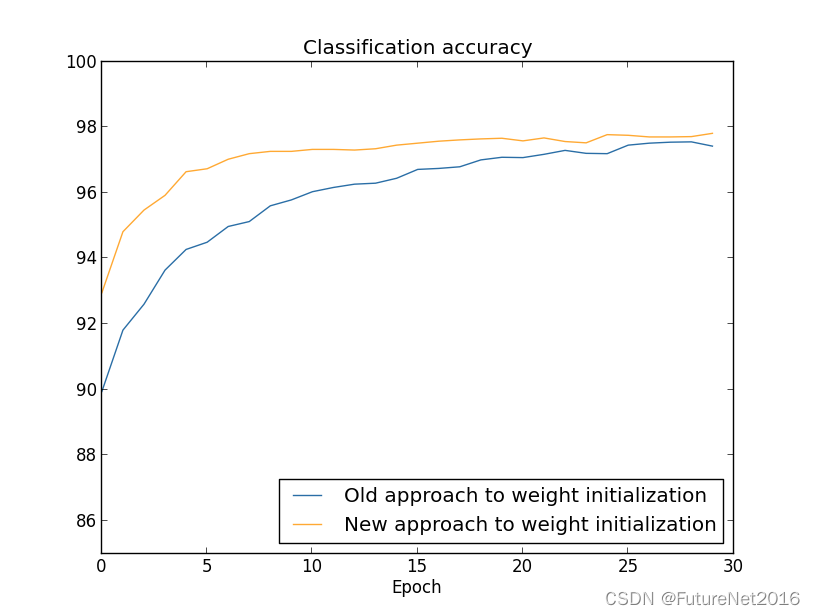
在这种情况下，这两条曲线并不完全相交。然而，我的实验表明，经过几个额外的训练周期（未显示），准确率几乎完全相同。因此，根据这些实验，似乎改进的权重初始化只是加速了学习过程，而没有改变我们网络的最终性能。然而，在第4章中，我们将看到一些神经网络的例子，其中采用了$1/\sqrt{n_{\mathrm{in}}}$权重初始化方法后，长期行为明显更好。因此，改进的权重初始化不仅改善了学习速度，有时还改善了最终性能。

$1/\sqrt{n_{\mathrm{in}}}$权重初始化方法有助于改进我们神经网络的学习方式。还提出了其他权重初始化技术，其中许多都建立在这个基本思想之上。我在这里不会回顾其他方法，因为$1/\sqrt{n_{\mathrm{in}}}$对我们的目的已经足够好了。如果你有兴趣深入了解，我建议查看Yoshua Bengio在2012年的一篇论文中关于第14和第15页的讨论，以及其中的参考文献。