文章目录
- ConKI:用于多模态情感分析的对比知识注入
- 文章信息
- 研究目的
- 研究内容
- 研究方法
- 1.总体结构
- 2.Encoding with Knowledge Injection
- 2.1 Pan-knowledge representations
- 2.2 Knowledge-specific representations
- 3.Hierarchical Contrastive Learning
- 4.损失函数
- 5.训练过程
- 结果与讨论
- 代码和数据集
- 附录
- 1.分层对比学习样本示例
- 2.Temperature Parameter
- 3.分层对比损失原理解释
ConKI:用于多模态情感分析的对比知识注入
总结:提出了一种利用知识注入和分层对比学习来获取更有效的单模态表征的方法。
文章信息
作者:Yakun Yu,Mingjun Zhao
单位:University of Alberta(艾伯塔大学,加拿大)
会议/期刊:Findings of the Association for Computational Linguistics(ACL 2023)(CCF A)
题目:ConKI: Contrastive Knowledge Injection for Multimodal Sentiment Analysis
年份:2023
研究目的
现有的多模态情感分析方法主要基于预训练模型获得的一般知识对模态进行编码,来进行多模态融合和表征学习,从而忽略了特定领域知识的影响。
研究内容
提出了用于多模态情感分析的对比知识注入框架(ConKI),用于学习泛知识表征(来自预训练模型提取的一般知识,如BERT)和特定知识表征(从相关外部数据源获得的领域特定知识)。
- 通过基于适配器架构的知识注入,每种模态不仅学习到一般知识表征,还能学习到来自外部数据源的特定领域知识表征。
- 使用分层对比学习,在单模态内不同知识类型之间、单个样本内不同模态之间、不同样本之间进行对比学习,促进模型学习更有效的特定知识与泛知识表征,从而改善多模态情感预测性能。
研究方法
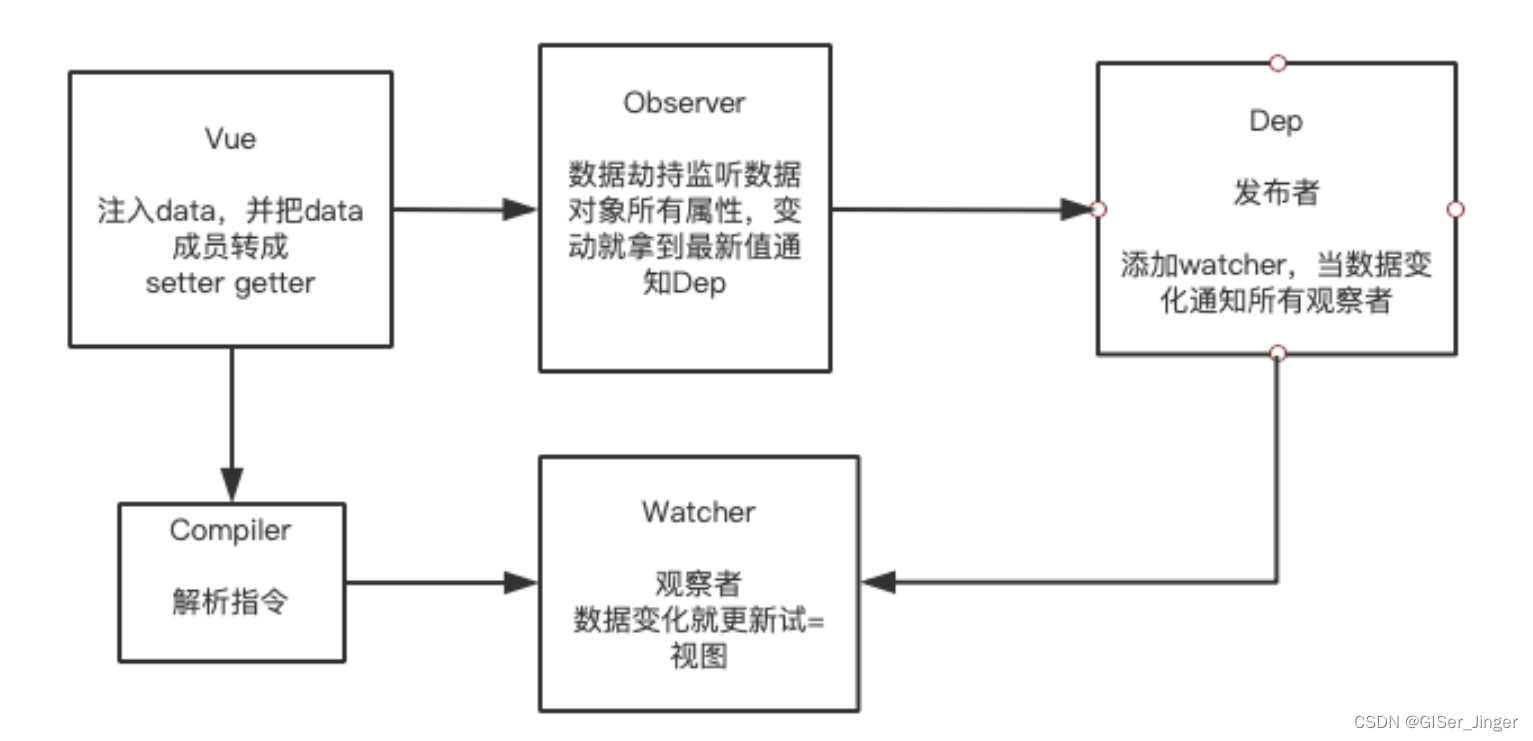
1.总体结构

首先处理原始多模态输入,得到对应的低级特征序列 I m ∈ { t , v , a } I_{m\in\{t,v,a\}} Im∈{t,v,a}。然后将每种模态的低级特征 I m I_m Im编码为特定知识表征 A m A_m Am和泛知识表征 O m O_m Om,其中 A m A_m Am由适配器Adapter的知识注入模型生成,而 O m O_m Om由预训练模型生成(文本使用BERT编码器,视频/音频使用随机初始化的Transformer编码器)。最后,ConKI同时在下游目标数据集上执行两个任务,即主要的MSA回归任务和辅助的分层对比学习子任务。
-
MSA任务
在MSA任务中,首先将每种模态的特定知识表征 A m A_m Am和泛知识表征 O m O_m Om合并起来。然后通过全连接 FC 进行内模态融合。接着使用融合网络 Fusion Network 实现跨模态融合。最后将融合后的表征送入多层感知器 MLP,产生情感预测值 y ^ \hat{y} y^.

-
分层对比学习任务
在知识层面、模态层面和样本层面构建负样本和正样本配对。通过整合这些分层对比,ConKI能够全面捕捉表征之间的动态变化,配对策略如下:
-
由于 A m A_m Am和 O m O_m Om能够捕捉到不同的知识,因此将它们分离开来,使它们相互补充,从而通过知识层面的对比获得更丰富的模态表征。
-
由于视频的情感是由所有模态决定的,因此通过模态级对比来学习六种表征的共性。
-
表达相似情感的视频应具有一定的相关性,因此通过样本级对比来捕捉相关性,以帮助进一步学习情绪接近的样本之间的共性。
-
| 符号 | 含义 |
|---|---|
| t , v , a t,v,a t,v,a | 文本模态,视觉模态,音频模态 |
| I t ∈ R l t × d t I_{t}\in\mathbb{R}^{l_{t}\times d_{t}} It∈Rlt×dt | 文本模态对应的低级特征序列 |
| I v ∈ R l v × d v I_{v}\in\mathbb{R}^{l_{v}\times d_{v}} Iv∈Rlv×dv | 视觉模态对应的低级特征序列 |
| I a ∈ R l a × d a I_a\in\mathbb{R}^{l_a\times d_a} Ia∈Rla×da | 音频模态对应的低级特征序列 |
| l m ∈ { t , v , a } l_{m\in\{t,v,a\}} lm∈{t,v,a} | 每个模态的序列长度 |
| d m ∈ { t , v , a } d_{m\in\{t,v,a\}} dm∈{t,v,a} | 特征向量维度 |
| A m ∈ { t , v , a } A_{m\in\{t,v,a\}} Am∈{t,v,a} | 特定知识表征 |
| O m ∈ { t , v , a } O_{m\in\{t,v,a\}} Om∈{t,v,a} | 泛知识表征 |
2.Encoding with Knowledge Injection
通过预训练编码器将每种模态编码为泛知识表征 O m O_m Om,通过适配器将每种模态编码为特定知识表征 A m A_m Am。
2.1 Pan-knowledge representations
使用预训练的BERT对文本模态进行编码,最后一层的POOL输出作为文本模态的泛知识表征
O
t
O_t
Ot。使用transformer的编码器对音频模态和视频模态进行编码,捕捉音频模态和视觉模态的泛知识表征
O
v
,
O
a
O_v,O_a
Ov,Oa。
O
t
,
H
t
=
Bert
(
I
t
;
θ
t
Bert
)
O
m
,
H
m
=
Encoder
(
I
m
;
θ
m
encoder
)
,
m
∈
{
v
,
a
}
O_t,H_t=\operatorname{Bert}(I_t;\theta_t^{\text{Bert}}) \\ O_m,H_m=\text{Encoder}(I_m;\theta_m^\text{encoder}),m\in\{v,a\}
Ot,Ht=Bert(It;θtBert)Om,Hm=Encoder(Im;θmencoder),m∈{v,a}
符号含义:
H
m
,
m
∈
{
t
,
a
,
v
}
H_m, m\in\{t,a,v\}
Hm,m∈{t,a,v}代表所有层的隐藏状态。
2.2 Knowledge-specific representations
通过知识注入模型(适配器)从外部多模态来源注入特定领域知识,适配器的输出作为各模态的特定知识表征 A t , A a , A v A_t,A_a,A_v At,Aa,Av。

Adapter由多个模块组成(两个FC层,中间有两个transformer层),每个模块可以插入到预训练编码器的任何transformer层之前(每个模态的适配器插入到各自预训练的编码器外部)。
每个模块都将预训练编码器的中间隐藏层状态和前一个适配器模块的输出作为输入。
A
m
=
Adapter
(
H
m
;
θ
m
adapter
)
,
m
∈
{
t
,
v
,
a
}
A_m=\text{Adapter}(H_m;\theta_m^\text{adapter}),m\in\{t,v,a\}
Am=Adapter(Hm;θmadapter),m∈{t,v,a}
【注】:在外部数据集上仅用MSA任务预训练各模态的适配器,然后利用预训练的适配器为下游目标任务(既包括MSA任务又包括分层对比学习子任务)生成特定知识表征
A
m
A_m
Am。
3.Hierarchical Contrastive Learning
-
单模态内不同知识类型对比(拉远)
泛知识表征和特定知识表征应相互分离,因为它们属于不同的知识领域,旨在相互补充。这种情况既存在于每个样本内部(i 和 j 代表同一个样本),也存在于批次中的不同样本之间(i 和 j 代表两个不同的样本)。因此,在一个批次中建立知识间负对:
N 1 i = { ( O m i , A n j ) ∣ m , n ∈ { t , v , a } & i , j ∈ B } ; \begin{gathered}\mathcal{N}_1^i=\{(O_m^i,A_n^j) \mid m,n\in\{t,v,a\}\&i,j\in B\};\end{gathered} N1i={(Omi,Anj)∣m,n∈{t,v,a}&i,j∈B}; -
单个样本内不同模态对比(拉近)
对于单个视频样本 i,所有模态都有说话者的共同动机,这些动机决定了整体情感。不同模态的泛知识表征代表相似的含义,因此需要拉近彼此的距离。同样对于特定知识表征,不同模态的特定知识表征也代表相似的含义,也需要拉近之间的距离。因此,建立样本内泛知识表征正对与特定知识表征正对。
P 1 i = { ( O m i , O n i ) , ( A m i , A n i ) ∣ m , n ∈ { t , v , a } & m ≠ n & i ∈ B } \mathcal{P}_1^i=\{(O_m^i,O_n^i),(A_m^i,A_n^i) \mid m,n\in\{t,v,a\} \& m\neq n\&i\in B\} P1i={(Omi,Oni),(Ami,Ani)∣m,n∈{t,v,a}&m=n&i∈B} -
不同样本间的对比(相同情感拉近,不同情感拉远)
情感接近与否的判断标准是:将不同样本的情感分数进行四舍五入的取整,相同即为接近,反之亦然。
- 对于情感接近的两个任意样本 i 和 j,样本 i 的六个表征应该接近样本 j 对应的六个表征。因此,建立不同样本之间表征的正对。
P 2 i = { ( O m i , O n j ) , ( A m i , A n j ) ∣ m , n ∈ { t , v , a } & r ( y i ) = r ( y j ) & i , j ∈ B & i ≠ j } \mathcal{P}_2^i = \{(O_m^i,O_n^j),(A_m^i,A_n^j)|\quad m,n\in\{t,v,a\}\&r(y^i)=r(y^j)\&i,j\in B\&i\neq j\} P2i={(Omi,Onj),(Ami,Anj)∣m,n∈{t,v,a}&r(yi)=r(yj)&i,j∈B&i=j}
- 对于情感不接近的两个任意样本 i 和 j,样本 i 的六个表征应该远离样本 j 的六个表征。因此,建立不同样本之间表征的负对。
N 2 i = { ( O m i , O n j ) , ( A m i , A n j ) ∣ m , n ∈ { t , v , a } & r ( y i ) ≠ r ( y j ) & i , j ∈ B & i ≠ j } \mathcal{N}_2^i = \{(O_m^i,O_n^j),(A_m^i,A_n^j)|\quad m,n\in\{t,v,a\}\&r(y^i)\neq r(y^j)\&i,j\in B\&i\neq j\} N2i={(Omi,Onj),(Ami,Anj)∣m,n∈{t,v,a}&r(yi)=r(yj)&i,j∈B&i=j}
| 符号 | 含义 |
|---|---|
| y i y^i yi | 代表样本 i 的真实标签 |
| r ( ⋅ ) r(\cdot) r(⋅) | 代表取整函数 |
| B B B | 代表批次 |
分层对比学习样本示例,对上面理论知识的解释
4.损失函数
整体损失:
L
=
L
t
a
s
k
+
λ
L
c
o
n
\mathcal{L}=\mathcal{L}_{task}+\lambda\mathcal{L}_{con}
L=Ltask+λLcon
MSA 任务损失:(均方误差计算)
L
t
a
s
k
=
1
∣
B
∣
∑
i
∣
B
∣
(
y
^
i
−
y
i
)
2
\mathcal{L}_{task}=\frac1{|B|}\sum_i^{|B|}(\hat{y}^i-y^i)^2
Ltask=∣B∣1i∑∣B∣(y^i−yi)2
分层对比损失:
分层对比损失函数将正样本对拉近,将负样本对推远。
L
c
o
n
=
∑
i
∈
B
−
1
∣
P
1
i
∪
P
2
i
∣
×
∑
(
p
,
q
)
∈
P
1
i
∪
P
2
i
log
f
(
(
p
,
q
)
)
∑
(
p
′
,
q
′
)
∈
A
l
l
P
a
i
r
s
f
(
(
p
′
,
q
′
)
)
\mathcal{L}_{con}=\sum_{i\in B}\frac{-1}{|\mathcal{P}_1^i\cup\mathcal{P}_2^i|}\times \sum_{(p,q)\in\mathcal{P}_1^i\cup\mathcal{P}_2^i}\log\frac{f((p,q))}{\sum_{(p^{\prime},q^{\prime})\in\mathsf{All~Pairs}}f((p^{\prime},q^{\prime}))}
Lcon=i∈B∑∣P1i∪P2i∣−1×(p,q)∈P1i∪P2i∑log∑(p′,q′)∈All Pairsf((p′,q′))f((p,q))
f ( ( p , q ) ) = exp ( p ∥ p ∥ 2 ⋅ q ∥ q ∥ 2 ⋅ 1 τ ) , All Pairs = P 1 i ∪ P 2 i ∪ N 1 i ∪ N 2 i . \begin{aligned}f((p,q))&=\exp(\frac p{\|p\|_2}\cdot\frac q{\|q\|_2}\cdot\frac1\tau),\\\\\text{All Pairs}&=\mathcal{P}_1^i\cup\mathcal{P}_2^i\cup\mathcal{N}_1^i\cup\mathcal{N}_2^i.\end{aligned} f((p,q))All Pairs=exp(∥p∥2p⋅∥q∥2q⋅τ1),=P1i∪P2i∪N1i∪N2i.
分层对比损失原理解释
| 符号 | 含义 |
|---|---|
| λ \lambda λ | 平衡MSA任务损失与分层对比学习损失的超参数 |
| $ | \mathcal{P}_1i\cup\mathcal{P}_2i |
| ( p , q ) (p,q) (p,q) | 表示对应集合中的一对,如 ( O t i , O v i ) (O_t^i,O_v^i) (Oti,Ovi) |
| τ \tau τ | 代表温度参数,temperature parameter |
| y y y | 真实标签 |
| y ^ \hat{y} y^ | 预测标签 |
| $ | B |
5.训练过程
首先使用外部数据集,同时固定预训练骨干的模型参数,通过 L t a s k \mathcal{L}_{task} Ltask损失函数,对ConKI中的适配器进行预训练。然后通过优化整体损失 L \mathcal{L} L,利用下游目标数据集对 ConKI 进行微调。


结果与讨论
⚠ 斜体是消融实验
- 通过与 SOTA 模型进行对比,证明了 ConKI 的效果最好,各项评估指标都优于以往的 SOTA 模型。
- 通过使用不同的模态组合,证明了使用三种模态的效果是最好的,验证了多模态的有效性。
- 通过对 ConKI 的四个组件(外部数据集的使用( C1 ),用于知识注入的适配器( C2 ),用于泛知识的预训练编码器( C3 )和分层对比学习( C4 ))进行消融,表明了 ConKI 的四个组件都是有效的。
- 通过去除分层对比学习中的知识间负对 N 1 \mathcal{N}_1 N1,表明 ConKI 学习区分泛知识和特定知识的表征对于分层对比学习至关重要。
- 通过将 ConKI 与经过外部数据集微调的 SOTA 模型进行比较,验证了 ConKI 模型在 MSA 任务上性能的提升不是来自外部数据集,而是与提出的知识注入和对比学习有关。
- 通过可视化在有无对比学习下的六种表征,证明了对比学习的有效性,通过对比学习能够学习到更好的表征。
代码和数据集
代码:未公开
数据集:CMU-MOSI,CMU-MOSEI,CH-SIMS
实验环境:NVIDIA RTX 2080Ti(11G)
附录
1.分层对比学习样本示例
示例批次由三个样本 ( { O t i , O v i , O a i , A t i , A v i , A a i } i = 1 , 2 , 3 ∈ B ) (\{O_t^i,O_v^i,O_a^i,A_t^i,A_v^i,A_a^i\}_{i=1,2,3}\in B) ({Oti,Ovi,Oai,Ati,Avi,Aai}i=1,2,3∈B)组成,其中样本 1 和样本 2 属于同一情感区间,而样本 3 属于不同的情感区间。(下图中的“1”代表行向量和列向量的正对。“0”代表行向量与列向量的负对)

-
单模态内不同知识类型对比(拉远)。上图蓝色方框中的“0”代表知识间的负对, N 1 B \mathcal{N}_1^{B} N1B。
-
单个样本内不同模态对比(拉近)。上图带有红色边框的“1”代表单样本模态之间的正对。
P 1 B = { ( O t 1 , O v 1 ) , ( O t 1 , O a 1 ) , ( O a 1 , O v 1 ) , ( A t 1 , A v 1 ) , ( A t 1 , A a 1 ) , ( A a 1 , A v 1 ) , ( O t 2 , O v 2 ) , ( O t 2 , O a 2 ) , ( O a 2 , O v 2 ) , ( A t 2 , A v 2 ) , ( A t 2 , A a 2 ) , ( A a 2 , A v 2 ) , ( O t 3 , O v 3 ) , ( O t 3 , O a 3 ) , ( O a 3 , O v 3 ) , ( A t 3 , A v 3 ) , ( A t 3 , A a 3 ) , ( A a 3 , A v 3 ) } ; \begin{aligned} \mathcal{P}_{1}^{B}=\{(O_{t}^{1},O_{v}^{1}),(O_{t}^{1},O_{a}^{1}),(O_{a}^{1},O_{v}^{1}), \\ (A_{t}^{1},A_{v}^{1}),(A_{t}^{1},A_{a}^{1}),(A_{a}^{1},A_{v}^{1}), \\ \begin{aligned}(O_{t}^{2},O_{v}^{2}),(O_{t}^{2},O_{a}^{2}),(O_{a}^{2},O_{v}^{2}),\end{aligned} \\ (A_t^2,A_v^2),(A_t^2,A_a^2),(A_a^2,A_v^2), \\ \begin{aligned}(O_t^3,O_v^3),(O_t^3,O_a^3),(O_a^3,O_v^3),\end{aligned} \\ (A_{t}^{3},A_{v}^{3}),(A_{t}^{3},A_{a}^{3}),(A_{a}^{3},A_{v}^{3})\}; \end{aligned} P1B={(Ot1,Ov1),(Ot1,Oa1),(Oa1,Ov1),(At1,Av1),(At1,Aa1),(Aa1,Av1),(Ot2,Ov2),(Ot2,Oa2),(Oa2,Ov2),(At2,Av2),(At2,Aa2),(Aa2,Av2),(Ot3,Ov3),(Ot3,Oa3),(Oa3,Ov3),(At3,Av3),(At3,Aa3),(Aa3,Av3)};
- 不同样本间的对比(相同情感拉近,不同情感拉远)。上图没有红色边框的“1“代表样本间相同情感的正对,蓝色边框外的“0”代表样本间不同情感的负对, N 2 B \mathcal{N}_2^{B} N2B。
P 2 B = { ( O t 1 , O t 2 ) , ( O t 1 , O v 2 ) , ( O t 1 , O a 2 ) , ( O v 1 , O t 2 ) , ( O v 1 , O v 2 ) , ( O v 1 , O a 2 ) , ( O a 1 , O t 2 ) , ( O a 1 , O v 2 ) , ( O a 1 , O a 2 ) , ( A t 1 , A t 2 ) , ( A t 1 , A v 2 ) , ( A t 1 , A a 2 ) , ( A v 1 , A t 2 ) , ( A v 1 , A v 2 ) , ( A v 1 , A a 2 ) , ( A a 1 , A t 2 ) , ( A a 1 , A v 2 ) , ( A a 1 , A a 2 ) } ; \begin{aligned} &&\mathcal{P}_{2}^{B}=\{(O_{t}^{1},O_{t}^{2}),(O_{t}^{1},O_{v}^{2}),(O_{t}^{1},O_{a}^{2}), \\ &&\begin{aligned}(O_{v}^{1},O_{t}^{2}),(O_{v}^{1},O_{v}^{2}),(O_{v}^{1},O_{a}^{2}),\end{aligned} \\ &&\begin{aligned}(O_{a}^{1},O_{t}^{2}),(O_{a}^{1},O_{v}^{2}),(O_{a}^{1},O_{a}^{2}),\end{aligned} \\ &&(A_{t}^{1},A_{t}^{2}),(A_{t}^{1},A_{v}^{2}),(A_{t}^{1},A_{a}^{2}), \\ &&(A_{v}^{1},A_{t}^{2}),(A_{v}^{1},A_{v}^{2}),(A_{v}^{1},A_{a}^{2}), \\ &&(A_{a}^{1},A_{t}^{2}),(A_{a}^{1},A_{v}^{2}),(A_{a}^{1},A_{a}^{2})\}; \end{aligned} P2B={(Ot1,Ot2),(Ot1,Ov2),(Ot1,Oa2),(Ov1,Ot2),(Ov1,Ov2),(Ov1,Oa2),(Oa1,Ot2),(Oa1,Ov2),(Oa1,Oa2),(At1,At2),(At1,Av2),(At1,Aa2),(Av1,At2),(Av1,Av2),(Av1,Aa2),(Aa1,At2),(Aa1,Av2),(Aa1,Aa2)};
2.Temperature Parameter
深度学习中的温度参数(Temperature Parameter)是什么?点击跳转查看
3.分层对比损失原理解释
L c o n = ∑ i ∈ B − 1 ∣ P 1 i ∪ P 2 i ∣ × ∑ ( p , q ) ∈ P 1 i ∪ P 2 i log f ( ( p , q ) ) ∑ ( p ′ , q ′ ) ∈ A l l P a i r s f ( ( p ′ , q ′ ) ) \mathcal{L}_{con}=\sum_{i\in B}\frac{-1}{|\mathcal{P}_1^i\cup\mathcal{P}_2^i|}\times \sum_{(p,q)\in\mathcal{P}_1^i\cup\mathcal{P}_2^i}\log\frac{f((p,q))}{\sum_{(p^{\prime},q^{\prime})\in\mathsf{All~Pairs}}f((p^{\prime},q^{\prime}))} Lcon=i∈B∑∣P1i∪P2i∣−1×(p,q)∈P1i∪P2i∑log∑(p′,q′)∈All Pairsf((p′,q′))f((p,q))
f ( ( p , q ) ) = exp ( p ∥ p ∥ 2 ⋅ q ∥ q ∥ 2 ⋅ 1 τ ) , All Pairs = P 1 i ∪ P 2 i ∪ N 1 i ∪ N 2 i . \begin{aligned}f((p,q))&=\exp(\frac p{\|p\|_2}\cdot\frac q{\|q\|_2}\cdot\frac1\tau),\\\\\text{All Pairs}&=\mathcal{P}_1^i\cup\mathcal{P}_2^i\cup\mathcal{N}_1^i\cup\mathcal{N}_2^i.\end{aligned} f((p,q))All Pairs=exp(∥p∥2p⋅∥q∥2q⋅τ1),=P1i∪P2i∪N1i∪N2i.
分层对比损失函数
L
c
o
n
\mathcal{L}_{con}
Lcon其实可以看做是带有temperature parameter的softmax loss损失函数的改写。
Softmax Loss
=
−
1
N
∑
i
=
1
N
∑
k
=
1
K
y
i
,
k
log
(
exp
(
z
i
,
k
/
T
)
∑
j
=
1
K
exp
(
z
i
,
j
/
T
)
)
\text{Softmax Loss}=-\frac1N\sum_{i=1}^N\sum_{k=1}^Ky_{i,k}\log\left(\frac{\exp(z_{i,k}/T)}{\sum_{j=1}^K\exp(z_{i,j}/T)}\right)
Softmax Loss=−N1i=1∑Nk=1∑Kyi,klog(∑j=1Kexp(zi,j/T)exp(zi,k/T))
∣ P 1 i ∪ P 2 i ∣ |\mathcal{P}_1^i\cup\mathcal{P}_2^i| ∣P1i∪P2i∣表示一个批次B中与样本 i 正对的个数,相当于softmax loss中的 N N N。某种意思上, ∣ P 1 i ∪ P 2 i ∣ |\mathcal{P}_1^i\cup\mathcal{P}_2^i| ∣P1i∪P2i∣也是一个不变的值。
log f ( ( p , q ) ) ∑ ( p ′ , q ′ ) ∈ A l l P a i r s f ( ( p ′ , q ′ ) ) \log\frac{f((p,q))}{\sum_{(p^{\prime},q^{\prime})\in\mathsf{All~Pairs}}f((p^{\prime},q^{\prime}))} log∑(p′,q′)∈All Pairsf((p′,q′))f((p,q)),相当于softmax loss中的 log ( exp ( z i , k / T ) ∑ j = 1 K exp ( z i , j / T ) ) \log\left(\frac{\exp(z_{i,k}/T)}{\sum_{j=1}^K\exp(z_{i,j}/T)}\right) log(∑j=1Kexp(zi,j/T)exp(zi,k/T)),都是用的softmax函数的思想。
f ( ( p , q ) ) = exp ( p ∥ p ∥ 2 ⋅ q ∥ q ∥ 2 ⋅ 1 τ ) f((p,q))=\exp(\frac p{\|p\|_2}\cdot\frac q{\|q\|_2}\cdot\frac1\tau) f((p,q))=exp(∥p∥2p⋅∥q∥2q⋅τ1),类比于 exp ( z i , k / T ) \exp(z_{i,k}/T) exp(zi,k/T),不过不同的是前者计算的是余弦距离得分,后者是logits得分。
所以二者思想是类似的。
分层对比损失函数 L c o n \mathcal{L}_{con} Lcon有效是因为:公式里面计算的,简单的说是正对之间的距离得分,我们想让距离得分越来越大,这样总体的损失就越来越小了。通过反向传播,就实现了这一问题。所以 L c o n \mathcal{L}_{con} Lcon有效。
😃😃😃