期权波动率是什么？怎么计算？

news2025/1/22 15:45:44

期权波动率

历史波动率：基于历史行情计算出来的历史波动率

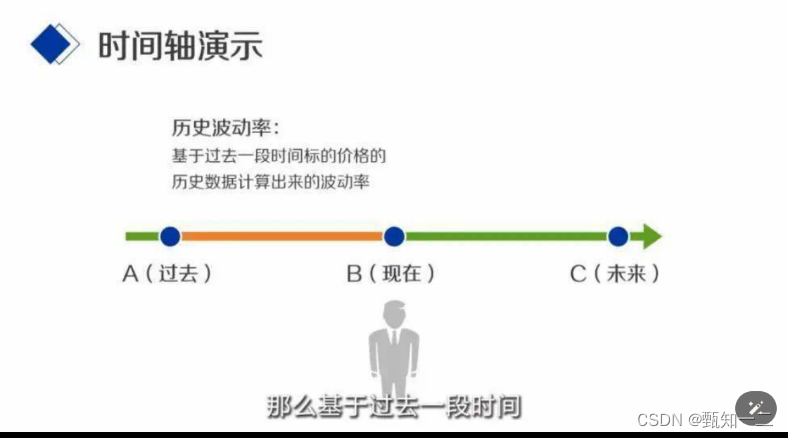
我们现在站在现实时点B回顾过去，从A到B这段时间的历史行情我们是知道的，但是基于过去一段时间，标的价格的历史数据计算出来的波动率，就是历史波动率，上面例子中X和Y股票的波动率，就属于历史波动率。

历史波动率用来反映标的价格，在过去一段时间的波动水平
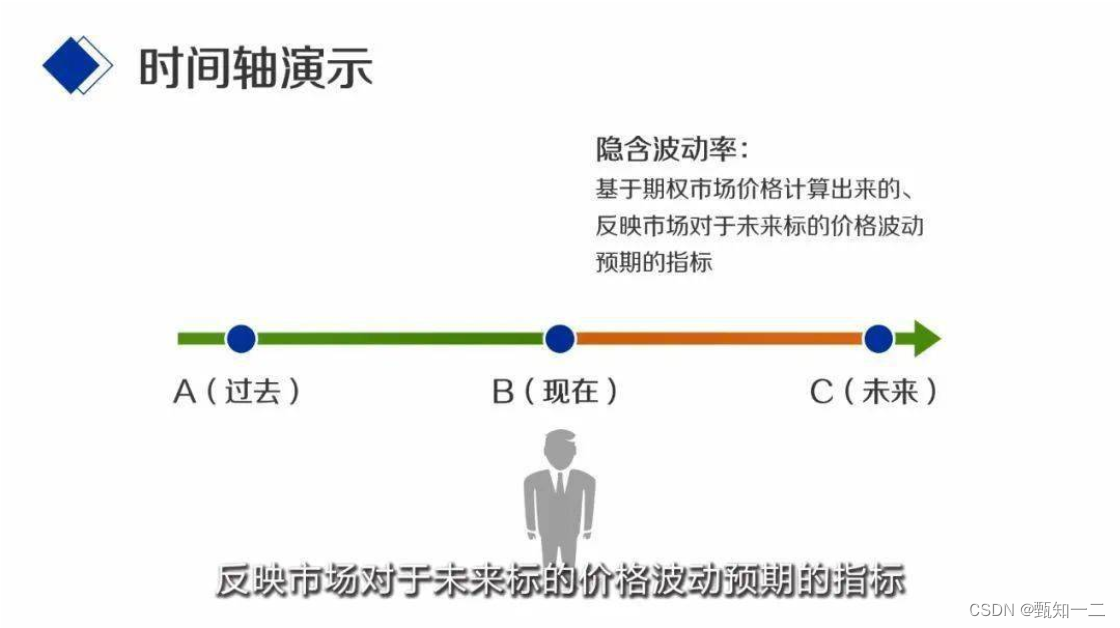
隐含波动率：预测的波动率

同样站在现在这个时间点B我们不仅可以回顾过去，还可以展望未来，虽然未来的标的价格我们不得而知，但是我们可以通过期权市场去发现投资者对于标的价格来来一段时间波动水平的普遍预期，这种基于期权市场价格计算出来的，反映市场对于未来标的价格波动预期的指标，这就是隐含波动率。

例如X公司股票期权以24%的隐含波动率进行交易，而Y公司股票以8%的隐含波动率进行交易，这就反映了出来市场中的一个观点，那就是市场普遍认为，未来X公司股票比Y公司股票的波动性更强。

在这里插入图片描述

已实现波动率：从未来看，波动率的真实值

表示未来的一段时间内，标的价格波动的真实水平，如果我们站在未来时点C，那么它就是历史波动率，但是我们是出于现在这个时点B，因此我们并不能准确的计算出已实现波动率。

已实现波动率通常用于和隐含波动率进行对比，反映出投资者对未来的预期是否准确，换言之就是投资者交易期权是否会盈利。

在这里插入图片描述

隐含波动率计算

def calculateImpv(price, s, k, r, t, cp):
    """计算隐含波动率"""
    # 检查期权价格必须为正数
    if price <= 0:
        return 0
    # 检查期权价格是否满足最小价值（即到期行权价值）
    meet = False
    if cp == 1 and (price > (s - k) * exp(-r * t)):
        meet = True
    elif cp == -1 and (price > k * exp(-r * t) - s):
        meet = True
    # 若不满足最小价值，则直接返回0
    if not meet:
        return 0
    # 采用Newton Raphson方法计算隐含波动率
    v = 0.29 # 初始波动率猜测
    for i in range(50):
        # 计算当前猜测波动率对应的期权价格和vega值
        p = calculatePrice(s, k, r, t, v, cp)
        vega = calculateOriginalVega(s, k, r, t, v, cp)
        
        # 如果vega过小接近0，则直接返回
        if not vega:
            break
        # 计算误差
        dx = (price - p) / vega
        # 检查误差是否满足要求，若满足则跳出循环
        if abs(dx) < DX_TARGET:
            break
        # 计算新一轮猜测的波动率
        v += dx
    # 检查波动率计算结果非负
    if v <= 0:
        return 0
    # 保留4位小数
    v = round(v, 4)
    return v


def calculateOriginalVega(s, k, r, t, v, cp):
    """计算原始vega值"""    
    price1 = calculatePrice(s, k, r, t, v*STEP_UP, cp)
    price2 = calculatePrice(s, k, r, t, v*STEP_DOWN, cp)
    vega = (price1 - price2) / (v * STEP_DIFF)
    return vega
    
def calculatePrice(s, k, r, t, v, cp):
    """计算期权价格"""
    # 如果波动率为0，则直接返回期权空间价值
    if v <= 0:
        return max(0, cp * (s - k))
    d1 = (log(s / k) + (r + 0.5 * pow(v, 2)) * t) / (v * sqrt(t))
    d2 = d1 - v * sqrt(t)
    price = cp * (s * cdf(cp * d1) - k * cdf(cp * d2) * exp(-r * t))
    return price

这个函数的计算过程结合了Newton-Raphson方法和Black-Scholes公式。Black-Scholes公式是一种用来计算欧式期权价格的公式，而Newton-Raphson method是一种用来求解方程根的迭代方法。

在这个函数中，通过解Black-Scholes方程来计算隐含波动率。

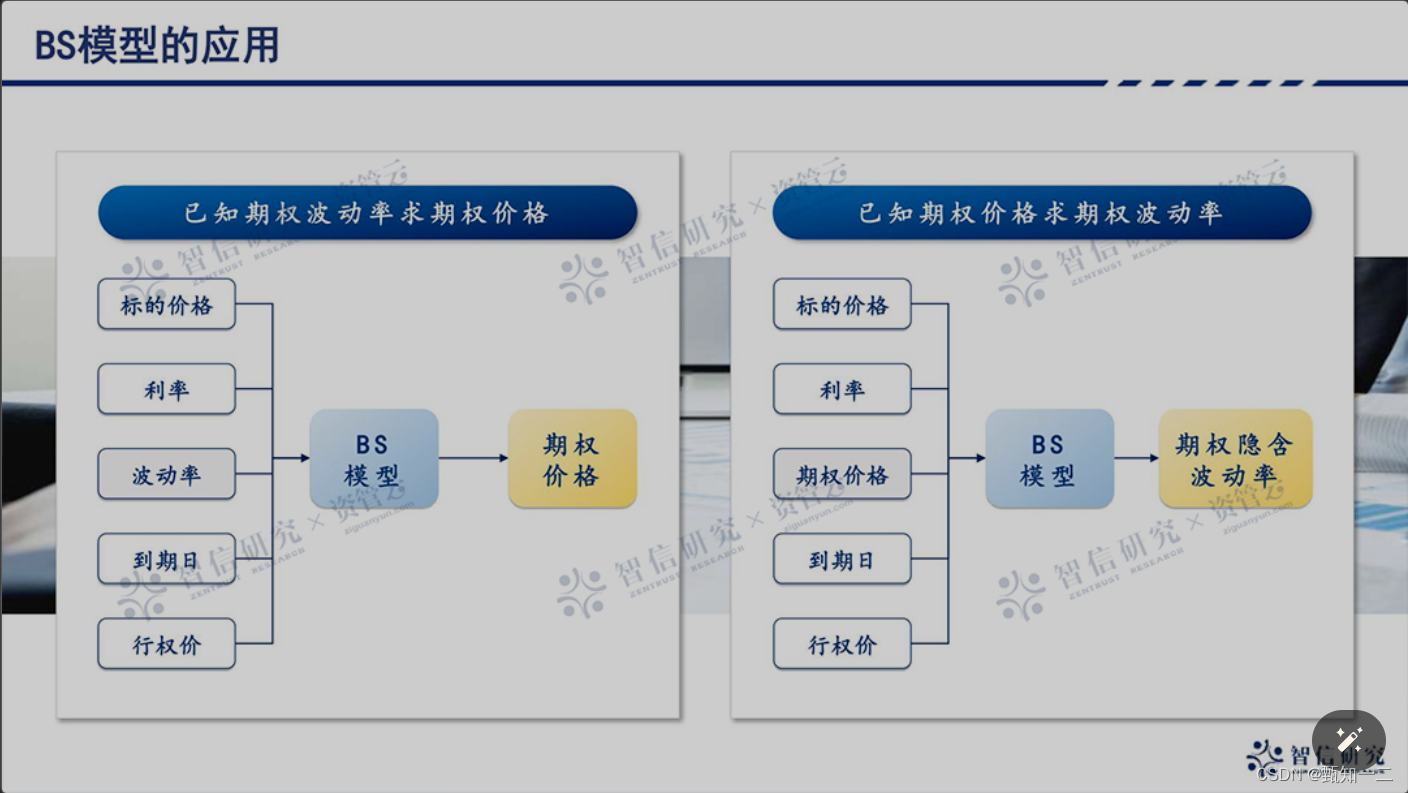
BS公式通俗解答

具体来说，Black-Scholes方程是一个偏微分方程，描述了欧式期权价格C（s,t）与基础标的资产价格St、时间t、波动率、行权价格K和无风险利率r之间的关系。通过解这个方程，我们可以找到一个隐含波动率值，使得期权价格与方程的解相等

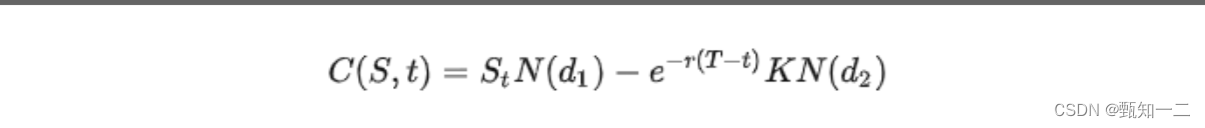
在这里插入图片描述
这里一共定义了三个函数：calculateImpv，calculateOriginalVega和calculatePrice，分别用于计算隐含波动率、原始vega值以及期权价格，可以看到该策略使用的正式Black-Scholes公式，首先检查波动率是否为0，如果为0，则直接返回期权的空间价值，即max(0, cp * (s - k))。这是因为当波动率为0时，期权价格只与基础资产价格和行权价格有关。

如果波动率不为0，那么会根据Black-Scholes公式计算出两个距离分布函数d1和d2，然后根据这些参数计算出期权价格。其中cp代表期权类型（1代表看涨期权，-1代表看跌期权），s代表基础资产价格，k代表行权价格，r代表无风险利率，t代表时间，v代表波动率。

同时在这个情境下，我们可以将期权价格视为一个函数，该函数关于波动率的一阶导数就是vega。因此，通过计算vega并对其进行迭代更新，我们可以更精确地估算出满足某个误差容忍度的波动率值。简单来说，vega在这里起到了一个桥梁的作用，帮助我们将期权价格与波动率联系起来，从而可以通过迭代方法找到合适的波动率值。

在这里插入图片描述