目录
- 一、力扣93.复原IP地址
- 1.1 题目
- 1.2 思路
- 1.3 代码
- 1.4 总结
- 二、力扣78.子集
- 2.1 题目
- 2.2 思路
- 2.3 代码
- 2.4 总结
- 三、力扣90.子集二
- 3.1 题目
- 3.2 思路
- 3.3 代码
- 3.4 总结
一、力扣93.复原IP地址
(比较困难,做起来很吃力)
1.1 题目

1.2 思路
同样是分割问题,不过本题需要在字符串上直接进行操作,由于String是不可修改的,所以需要借助StringBuilder来处理字符串的增减及拼接操作;
递归终止条件:设置pointCount来记录点的数量,当ip地址中已加入三个点时终止,然后记得再判断最后一段的有效性;
回溯:pointCount的减减以及删掉刚刚加入到字符串里的点;
1.3 代码
class Solution {
public List<String> res = new ArrayList<>();
public int pointCount = 0;//ip地址中点的数量
public List<String> restoreIpAddresses(String s) {
//java处理字符串用StringBuilder
StringBuilder str = new StringBuilder(s);
backTracking(str,0);
return res;
}
public void backTracking(StringBuilder str,int startIndex){
//递归终止条件
if(pointCount == 3){
//还剩最后一段的合法性未判断
if(isVaild(str,startIndex,str.length()-1)){
res.add(str.toString());
}
return;
}
//递归+回溯
for(int i = startIndex;i < str.length();i++){
if(isVaild(str,startIndex,i)){
//合法,那么加点切割
str.insert(i+1,".");
pointCount++;
backTracking(str,i+2);
str.deleteCharAt(i+1);
pointCount--;
}else{
break;
}
}
}
//判断字符串str[left,right]左闭右闭是否满足ip段要求
public boolean isVaild(StringBuilder str,int left,int right){
if(left > right){
return false;
}
//不能含有前导0
if(str.charAt(left) == '0' && left != right){
return false;
}
//介于0-255之间
int num = 0;
for(int i = left;i <= right ;i++){
if(str.charAt(i) < '0' || str.charAt(i) > '9'){
return false;
}
num = (num * 10) + (str.charAt(i)-'0');
if(num > 255){
return false;
}
}
return true;
}
}
1.4 总结
StringBuilder使用方法:https://blog.csdn.net/qq_50617271/article/details/112686826
判断ip段是否合法时的方法isVaild()中的循环: s[i],表示字符串中的一位,S【i】-0. 把字符串转化成数字。 num*10,是下一个循环的时候上一位数字要左移。假设s=【255】, 循环三次的结果就是 2->25->255.
二、力扣78.子集
2.1 题目

2.2 思路
如果把 子集问题、组合问题、分割问题都抽象为一棵树的话,那么组合问题和分割问题都是收集树的叶子节点,而子集问题是找树的所有节点!
自己的想法:和组合问题类似,不同的地方是树结构的每个结点的数据都要加入到结果集中,即path当中每加入一个元素就需要将path加入到res结果集里。
2.3 代码
class Solution {
public List<List<Integer>> res = new ArrayList<>();
public List<Integer> path = new ArrayList<>();
public List<List<Integer>> subsets(int[] nums) {
res.add(new ArrayList<>(path));//添加空集
backTracking(nums,0);
return res;
}
public void backTracking(int[] nums,int startIndex){
//递归终止条件
if(startIndex == nums.length){
return;
}
for(int i = startIndex; i< nums.length;i++){
path.add(nums[i]);
res.add(new ArrayList<>(path));
backTracking(nums,i+1);
path.remove(path.size()-1);
}
}
}
2.4 总结
如果把 子集问题、组合问题、分割问题都抽象为一棵树的话,那么组合问题和分割问题都是收集树的叶子节点,而子集问题是找树的所有节点!
三、力扣90.子集二
3.1 题目
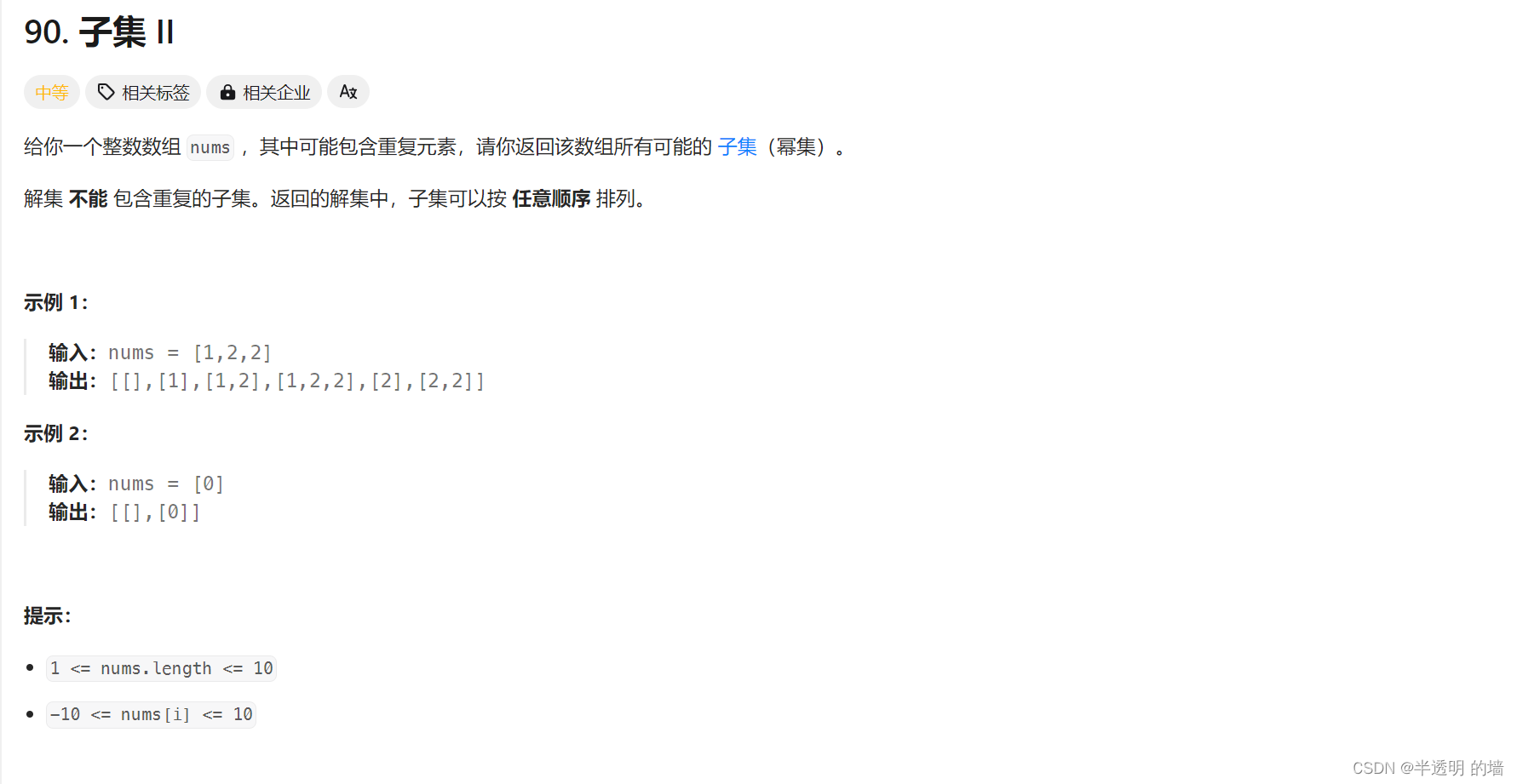
3.2 思路
在上一题子集问题的基础上多了个条件:可能包含重复元素,那么就需要先排序,然后按照树的结构横向去重,即兄弟之间去重。
3.3 代码
class Solution {
public List<List<Integer>> res = new ArrayList<>();
public List<Integer> path = new ArrayList<>();
boolean[] used;//记录数据元素是否使用过,用来去重
public List<List<Integer>> subsetsWithDup(int[] nums) {
used = new boolean[nums.length];
for(int i = 0;i<nums.length;i++){
used[i] = false;
}
//先向结果集中加入空集
res.add(new ArrayList<>(path));
//对原数组排序
Arrays.sort(nums);
backTracking(nums,0);
return res;
}
//递归回溯
public void backTracking(int[] nums,int startIndex){
//递归终止条件
if(startIndex == nums.length){
return;
}
for(int i = startIndex;i<nums.length;i++){
//兄弟去重
if(i!=0 && nums[i] == nums[i-1] && used[i-1] == false){
continue;
}
path.add(nums[i]);
res.add(new ArrayList<>(path));
used[i] = true;
backTracking(nums,i+1);
path.remove(path.size()-1);
used[i] = false;
}
}
}
3.4 总结
横向(兄弟)去重:注意是used[i-1] == false;即前一个相同的元素没有被用,也就是如果用当前位置元素的话汇合上一次for循环i-1的组合重复,所有要continue,避免重复,即横向(兄弟)去重。
//兄弟去重
if(i!=0 && nums[i] == nums[i-1] && used[i-1] == false){
continue;
}