题目描述：

n 个小朋友站成一排。

现在要把他们按身高从低到高的顺序排列，但是每次只能交换位置相邻的两个小朋友。

每个小朋友都有一个不高兴的程度。

开始的时候，所有小朋友的不高兴程度都是 0。

如果某个小朋友第一次被要求交换，则他的不高兴程度增加 1，如果第二次要求他交换，则他的不高兴程度增加 2（即不高兴程度为 3），依次类推。当要求某个小朋友第 k 次交换时，他的不高兴程度增加 k。

请问，要让所有小朋友按从低到高排队，他们的不高兴程度之和最小是多少。

如果有两个小朋友身高一样，则他们谁站在谁前面是没有关系的。

输入格式：

输入的第一行包含一个整数 n，表示小朋友的个数。

第二行包含 n 个整数 H1,H2,…,Hn分别表示每个小朋友的身高。

输出格式：

输出一行，包含一个整数，表示小朋友的不高兴程度和的最小值。

数据范围：

1≤n≤100000
0≤Hi≤1000000

输入样例：

3
3 2 1

输出样例：

9

样例解释：

首先交换身高为3和2的小朋友，再交换身高为3和1的小朋友，再交换身高为2和1的小朋友，每个小朋友的不高兴程度都是3，总和为9。

分析步骤：

  第一，看完题目我们可以得知，我们要一个一个将相邻的升高不符合位置的同学移动到正确的位置，并且要移动的次数最少。每个小朋友需要交换的次数是前面比它大的数和后面比它小的数，因为如果前面有比它大的数，那么它必定和前面的交换一次，使得前面大的数排到后面，同理可以知道比它小的数一定要和它交换到前面。这其实是一道求逆序对的题目，所以我们可以用归并排序解决这道题目。

  第二：书写主函数，构建整体框架。

              我们先将升高输入进数组 q 的第一个位置，再将他的第二个值定为 i ， 因为 i 为他站的位置，之后进行归并排序从第 0 个 位置到第 n - 1 个位置，进行枚举。解出答案后，因为每次增加的不高兴程度为1 ， 2 ， 3 ，4.........我们可以轻松看出来这是一个等差数列。所以最终用一个for循环，并且利用等差数列求和公式求出每个小朋友的不高兴程度并且相加，进行动态更新。

int main()
{
    cin>>n;
    for(int i = 0 ; i < n ; i ++){
        cin>>q[i].x;
        q[i].y = i;
    }
    merge(0 , n - 1);
    LL res = 0 ; 
    for(int i = 0 ; i < n ; i ++) res += (LL)sum[i] * (sum[i]+1)/2;
    cout<<res;
    return 0;
}

  第三：书写归并排序

             我们定义的 l ， r为我们归并排序的左右边界，所以如果当左边界大于了右边界的话就返回退出。

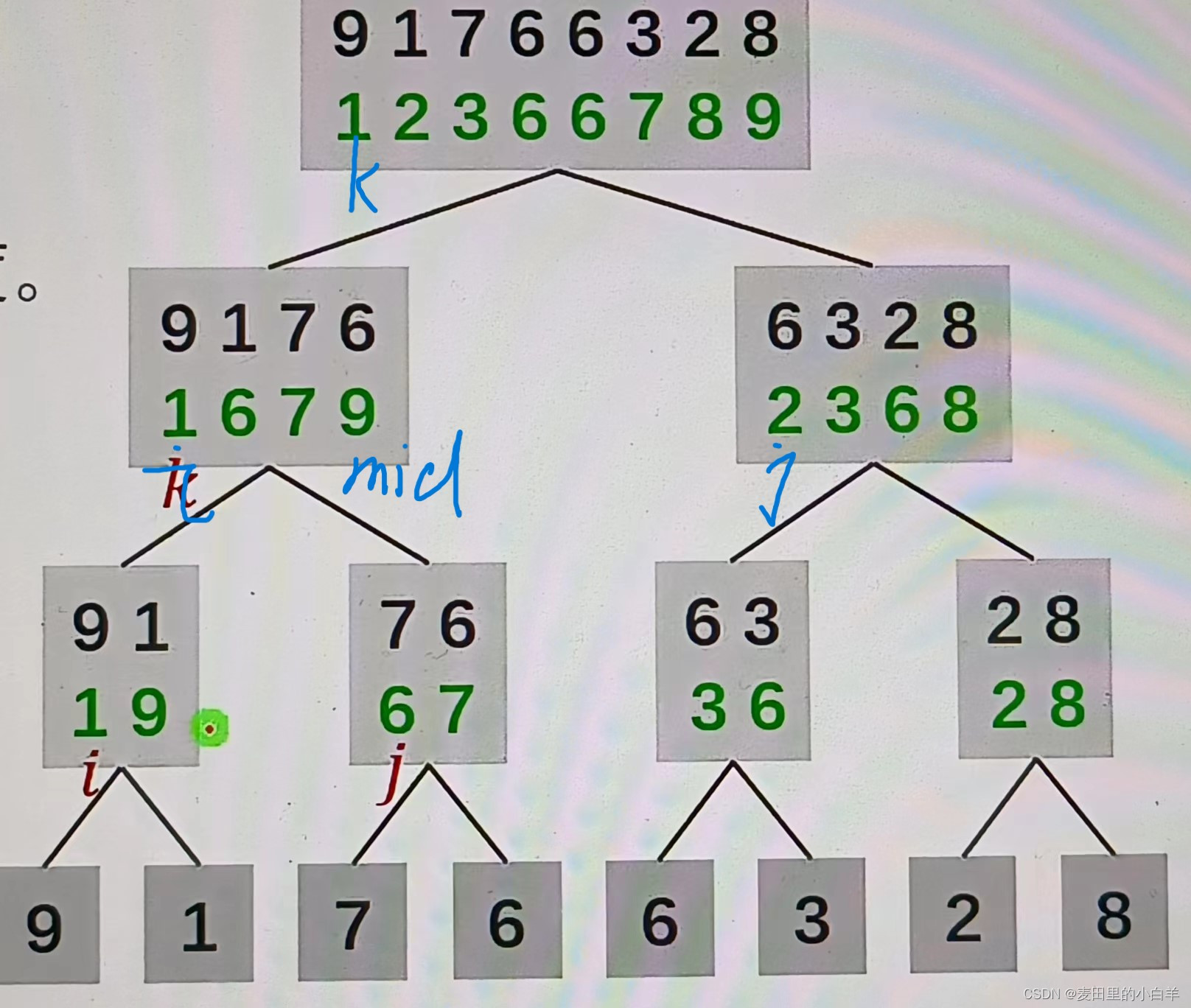
            求出 mid 将 i 赋值为 l ; j 赋值为 mid+1；看赋值为0；最后再将【l,mid】和【mid+1,r】进行归并排序，直到数字分为一个一个的。大家要始终清楚 i , j , k 代表的是什么，他们所在哪个位置。i左区间第一个数，j为右区间第一个数，k为新数组的第一个位置。这个新数组来存归并后的数据顺序。

            进入while循环注意判断条件只有 i <= mid and j <= r都符合条件时才可以继续循环，如果有一个不满足的话，就代表有一个数组已经全部被排好序了。

            如果左边区间的值 小于等于 右边区间的值的话，也就是前边小朋友的身高 小于 后边小朋友的身高，则这个小朋友需要被调整的次数时 j - mid - 1。为什么是这个值？因为表示当前元素q[i]不会产生逆序对。由于q[mid+1...j-1]的元素都大于等于q[i].x，所以与q[i]进行比较的时候，逆序对的数量为j - mid - 1。即在右半部分数组中，小于q[i].x的元素的数量。并且将这个值放入我们的新数组temp之中。

           如果左边区间的值 大于 右边区间的值的话，也就是前边小朋友的身高 大于 后边小朋友的身高是，则需要被调整的次数是 mid - i + 1。为什么是这个值？因为表示当前元素q[i]会产生逆序对，逆序对的数量是mid - i + 1，将这个数排到左边数组的最后，即在左半部分数组中，大于q[i].x的元素的数量。并且将这个值放入我们的新数组temp之中。

           倘若这个循环结束了的话，就代表着左边数组或者右边数组有一个已经排完了，这个时候我们就在遍历一下如果左边没有排序完，就进入while循环更新sum值（需要更换的次数）；如果右边没有排序完，我们就直接将其放入新数组，不要计算需要更换位置的次数，因为前边的已经排好序了，直接放入进去就行；

           最后将我们刚刚存好的tmp数组的值 ”还给“ 之前的q数组。

void merge(int l, int r)
{
    if(l >= r) return ;
    int mid = (l+r) / 2;
    int i = l , j = mid + 1 , k = 0;
    merge(l , mid) , merge(mid+1 , r);
    while(i <= mid and j <= r){
        if(q[i].x <= q[j].x ){
            sum[q[i].y] += j - mid - 1;
            tmp[k++] = q[i++];
        }
        else{
                sum[q[j].y] += mid - i + 1;
                tmp[k++] = q[j++];
        }
    }
    while(i <= mid){
        sum[q[i].y] += j- mid - 1 ;
        tmp[k++] = q[i++];
    }
    while(j <= r){
        tmp[k++] = q[j++];
    }
    for(int i = l , j = 0 ; i <= r ; j ++ , i ++){
        q[i] = tmp[j];
    }
}

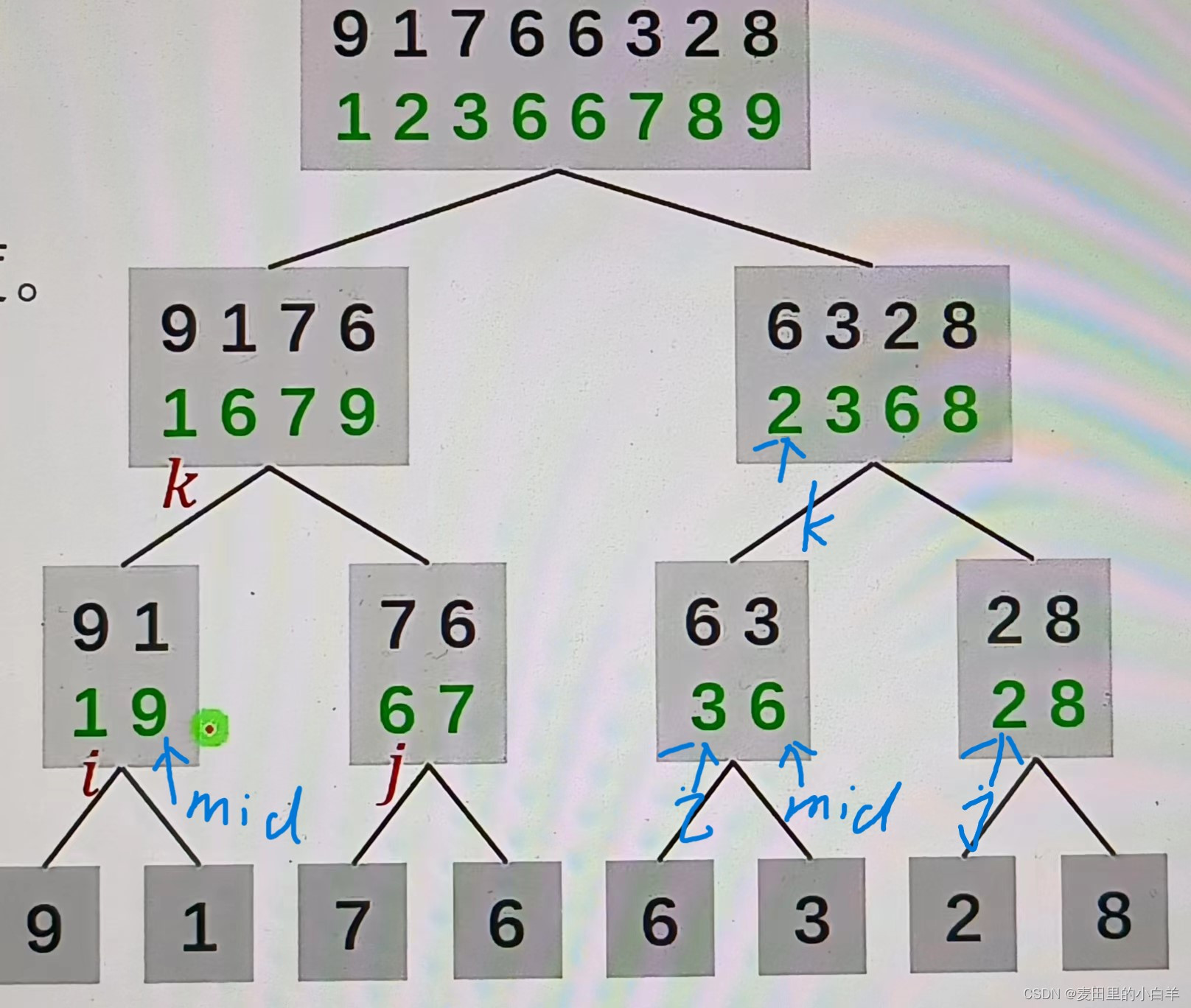
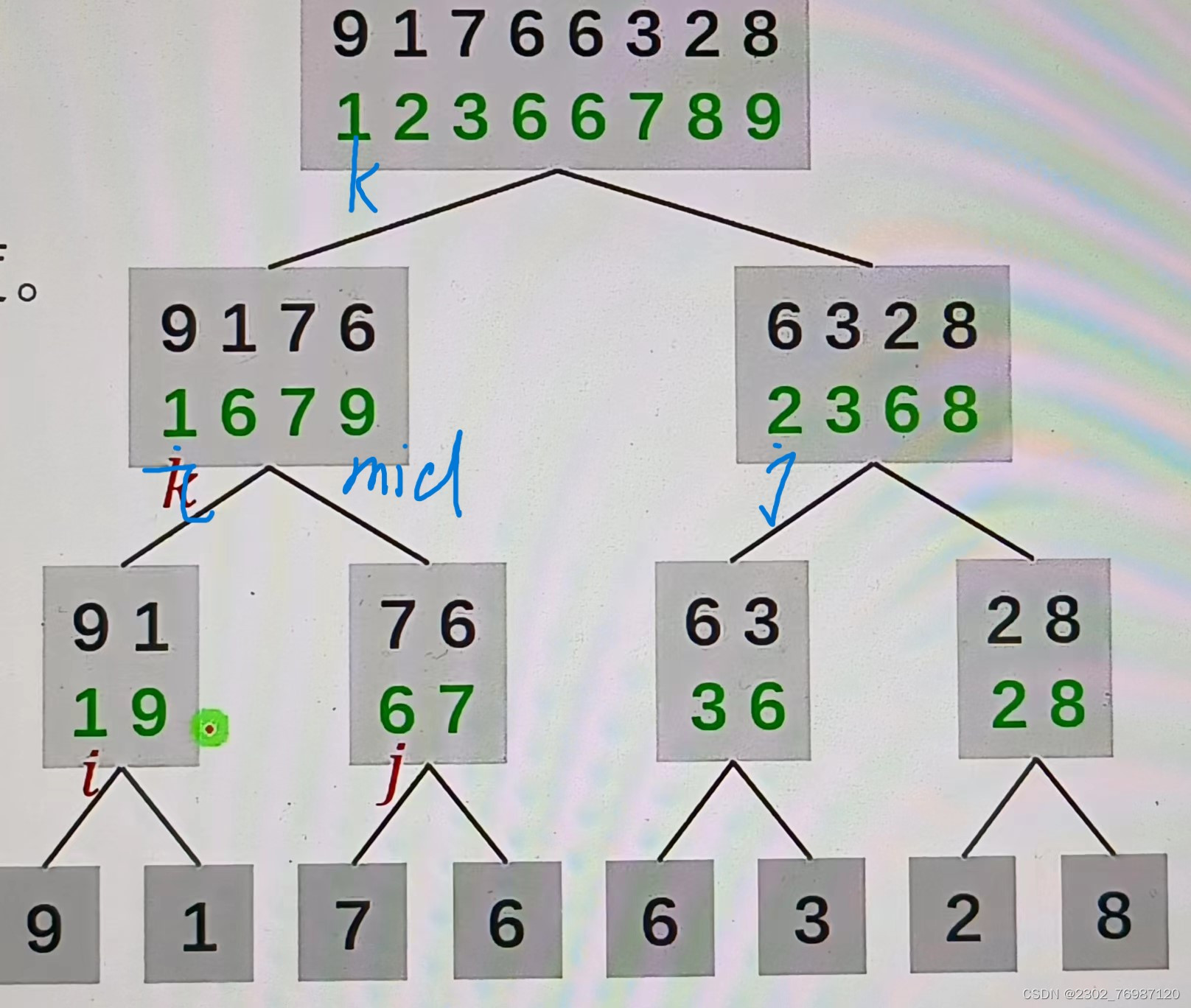
这两个图我给大家标出了i ， j ，k的位置，大家可以好好注意注意，对于不理解的位置变化的那个式子，也可以根据这个图自己动手写一些，纸上得来终觉浅，得知此事要躬行

代码：

#include <iostream>
#include <cstring>
#include <algorithm>
#define x first
#define y second
typedef long long LL;

using namespace std;
typedef pair<int, int> PII;

const int N = 1e5+10;
int  n;
PII q[N], tmp[N];
int sum[N];

void merge(int l, int r)
{
    if(l >= r) return ;
    int mid = (l+r) / 2;
    int i = l , j = mid + 1 , k = 0;
    merge(l , mid) , merge(mid+1 , r);
    while(i <= mid and j <= r){
        if(q[i].x <= q[j].x ){
            sum[q[i].y] += j - mid - 1;
            tmp[k++] = q[i++];
        }
        else{
                sum[q[j].y] += mid - i + 1;
                tmp[k++] = q[j++];
        }
    }
    while(i <= mid){
        sum[q[i].y] += j- mid - 1 ;
        tmp[k++] = q[i++];
    }
    while(j <= r){
        tmp[k++] = q[j++];
    }
    for(int i = l , j = 0 ; i <= r ; j ++ , i ++){
        q[i] = tmp[j];
    }
}

int main()
{
    cin>>n;
    for(int i = 0 ; i < n ; i ++){
        cin>>q[i].x;
        q[i].y = i;
    }
    merge(0 , n - 1);
    LL res = 0 ; 
    for(int i = 0 ; i < n ; i ++) res += (LL)sum[i] * (sum[i]+1)/2;
    cout<<res;
    return 0;
}