题目解析参考:验证二叉搜索树_哔哩哔哩_bilibili
一开始做呢,就跟这位老兄一样:


因为没有考虑到5和3的比较
接下来走入整体:
先根遍历解法:
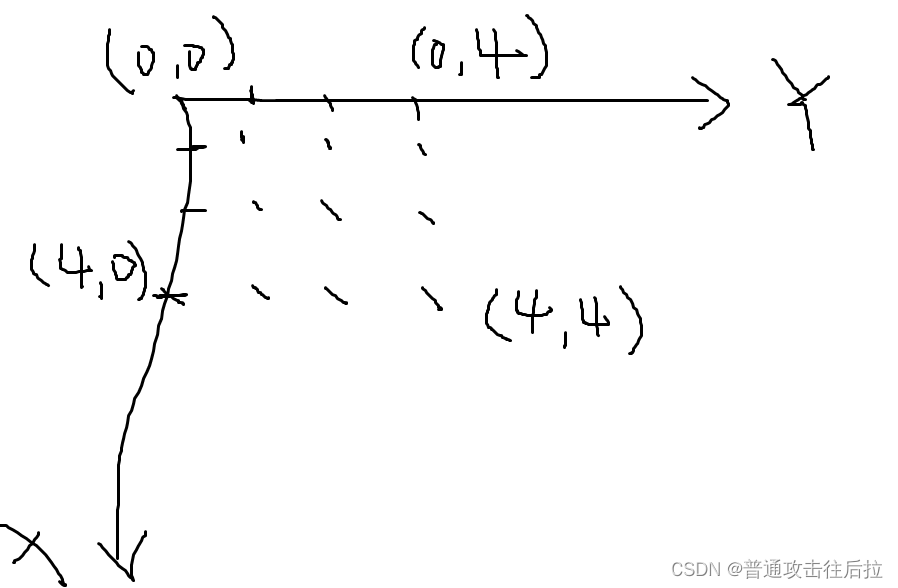
首先 每个点其实都有范围,比如根节点的范围在(-INF,INF),就拿上面图片举例子,4这个节点的范围应该是(-INF,5),所以先序遍历,我们要先比较根节点是否在他应该在的范围,其次判断左子树,接下来判断右子树。题目中的数据比较有趣,建议大家用LONG_MIN和LONG_MAX来定义-INF和INF。推荐博客:宏LONG_MAX和LLONG_MAX-CSDN博客
代码:
C++:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool dfs(TreeNode* root,long int left,long int right){
if(root==nullptr){return true;}
if(root->val<=left || root->val>=right){return false;}
if(dfs(root->left,left,root->val)==false){return false;}
if(dfs(root->right,root->val,right)==false){return false;}
return true;
}
bool isValidBST(TreeNode* root) {
return dfs(root,LONG_MIN,LONG_MAX);
}
};Python:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
def dfs(root:Optional[TreeNode],left:int,right:int) -> bool:
if root is None:
return True
if root.val<=left or root.val>=right:
return False
if dfs(root.left,left,root.val)==False:
return False
if dfs(root.right,root.val,right)==False:
return False
return True
return dfs(root,-float('INF'),float('INF'))需要注意的地方有:
Python中表示正无穷为:
-float('INF'),float('INF')参考博客为:python 中正无穷,负无穷的表示-CSDN博客
中根遍历解法:
中根遍历二叉搜索树得到的是有序数列,那么我们只需简单的判断上次判断的那个数是否小于正在判断的这个数即可。即先判断左子树,给出判断条件,再判断右子树。
代码:
C++:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
long pre=LONG_MIN;
bool isValidBST(TreeNode* root) {
if(root==nullptr){return true;}
if(isValidBST(root->left)==false){return false;}
if(root->val<=pre){return false;}
pre=root->val;
if(isValidBST(root->right)==false){return false;}
return true;
}
};Python:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
pre=-float("INF")
def isValidBST(self, root: Optional[TreeNode]) -> bool:
if root is None:
return True
if self.isValidBST(root.left)==False:
return False
if root.val<=self.pre:
return False
self.pre=root.val
if self.isValidBST(root.right)==False:
return False
return True注意这行代码,否则会出错:
self.pre=root.val后根遍历解法:
与力扣--二叉树的最近公共祖先-CSDN博客思路类似,都是把下面的左子树和右子树的最小值和最大值向上传,如果根节点的值小于等于左子树的最大值 或者 根节点的值大于等于右子树的最小值,那么这就不是个二叉搜索树(返回-INF,INF,最后判断根节点返回的两个值是不是-INF,INF即可)。那么向上传的值是什么呢,是这个子树的最小值以及最大值,最小值即为左子树的最小值和该节点的值取最小(为什么还要考虑该节点呢?因为有没有左子树的情况,此时左子树的最小值为INF,最大值为-INF),同理最大值即为右子树的最大值和该节点的值取最大。
代码:
C++:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
pair<long,long> dfs(TreeNode* root){
if(root==nullptr){return {LONG_MAX,LONG_MIN};}
auto[l_min,l_max]=dfs(root->left);
auto[r_min,r_max]=dfs(root->right);
//cout<<l_min<<' '<<l_max<<' '<<r_min<<' '<<r_max<<endl;
if(root->val<=l_max || root->val>=r_min){return {LONG_MIN,LONG_MAX};}
return {min(l_min,long(root->val)),max(r_max,long(root->val))};
}
bool isValidBST(TreeNode* root) {
auto[res_l,res_r]=dfs(root);
if(res_l==LONG_MIN){return false;}
return true;
}
};Python:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
def dfs(root:Optional[TreeNode]) -> Tuple:
if root is None:
return float("INF"),-float("INF")
l_min,l_max=dfs(root.left)
r_min,r_max=dfs(root.right)
if root.val<=l_max or root.val>=r_min:
return -float("INF"),float("INF")
return min(l_min,root.val),max(r_max,root.val)
res_l,res_r=dfs(root)
if res_l==-float("INF"):
return False
return True