LeetCode 每日一题 Day 102-108

2789. 合并后数组中的最大元素

给你一个下标从 0 开始、由正整数组成的数组 nums 。

你可以在数组上执行下述操作任意次：

选中一个同时满足 0 <= i < nums.length - 1 和 nums[i] <= nums[i + 1] 的整数 i 。将元素 nums[i + 1] 替换为 nums[i] + nums[i + 1] ，并从数组中删除元素 nums[i] 。
返回你可以从最终数组中获得的最大元素的值。

示例 1：

输入：nums = [2,3,7,9,3]
输出：21
解释：我们可以在数组上执行下述操作：

选中 i = 0 ，得到数组 nums = [5,7,9,3] 。
选中 i = 1 ，得到数组 nums = [5,16,3] 。
选中 i = 0 ，得到数组 nums = [21,3] 。
最终数组中的最大元素是 21 。可以证明我们无法获得更大的元素。
示例 2：

输入：nums = [5,3,3]
输出：11
解释：我们可以在数组上执行下述操作：

选中 i = 1 ，得到数组 nums = [5,6] 。
选中 i = 0 ，得到数组 nums = [11] 。
最终数组中只有一个元素，即 11 。

提示：

1 <= nums.length <= 1e5
1 <= nums[i] <= 1e6

暴力枚举能过：

class Solution {
public:
    long long maxArrayValue(vector<int>& nums) {
        long long sum = nums.back();
        for (int i = nums.size() - 2; i >= 0; i--) {
            sum = nums[i] <= sum ? sum + nums[i] : nums[i];
        }
        return sum;
    }
};

2684. 矩阵中移动的最大次数

给你一个下标从 0 开始、大小为 m x n 的矩阵 grid ，矩阵由若干正整数组成。

你可以从矩阵第一列中的任一单元格出发，按以下方式遍历 grid ：

从单元格 (row, col) 可以移动到 (row - 1, col + 1)、(row, col + 1) 和 (row + 1, col + 1) 三个单元格中任一满足值严格大于当前单元格的单元格。
返回你在矩阵中能够移动的最大次数。

示例 1：

输入：grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
输出：3
解释：可以从单元格 (0, 0) 开始并且按下面的路径移动：

(0, 0) -> (0, 1).
(0, 1) -> (1, 2).
(1, 2) -> (2, 3).
可以证明这是能够移动的最大次数。
示例 2：

输入：grid = [[3,2,4],[2,1,9],[1,1,7]]
输出：0
解释：从第一列的任一单元格开始都无法移动。

提示：

m == grid.length
n == grid[i].length
2 <= m, n <= 1000
4 <= m * n <= 1e5
1 <= grid[i][j] <= 1e6

DFS或BFS都可做：

class Solution {
public:
    int maxMoves(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        int ans = 0;
        function<void(int, int)> dfs = [&](int i, int j) {
            ans = max(ans, j);
            if (ans == n - 1) {
                return;
            }
            for (int k = max(i - 1, 0); k < min(i + 2, m); k++) {
                if (grid[k][j + 1] > grid[i][j]) {
                    dfs(k, j + 1);
                }
            }
            grid[i][j] = 0;
        };
        for (int i = 0; i < m; i++) {
            dfs(i, 0);
        }
        return ans;
    }
};

BFS方法(灵神）：

class Solution {
public:
    int maxMoves(vector<vector<int>> &grid) {
        int m = grid.size(), n = grid[0].size();
        vector<int> vis(m, -1), q(m);
        iota(q.begin(), q.end(), 0);
        for (int j = 0; j < n - 1; j++) {
            vector<int> nxt;
            for (int i : q) {
                for (int k = max(i - 1, 0); k < min(i + 2, m); k++) {
                    if (vis[k] != j && grid[k][j + 1] > grid[i][j]) {
                        vis[k] = j; // 第 k 行目前最右访问到了 j
                        nxt.push_back(k);
                    }
                }
            }
            if (nxt.empty()) { // 无法再往右走了
                return j;
            }
            q = move(nxt);
        }
        return n - 1;
    }
};

310. 最小高度树

树是一个无向图，其中任何两个顶点只通过一条路径连接。换句话说，任何一个没有简单环路的连通图都是一棵树。

给你一棵包含 n 个节点的树，标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表（每一个边都是一对标签），其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。

可选择树中任何一个节点作为根。当选择节点 x 作为根节点时，设结果树的高度为 h 。在所有可能的树中，具有最小高度的树（即，min(h)）被称为最小高度树。

请你找到所有的最小高度树并按任意顺序返回它们的根节点标签列表。

树的高度是指根节点和叶子节点之间最长向下路径上边的数量。

示例 1：

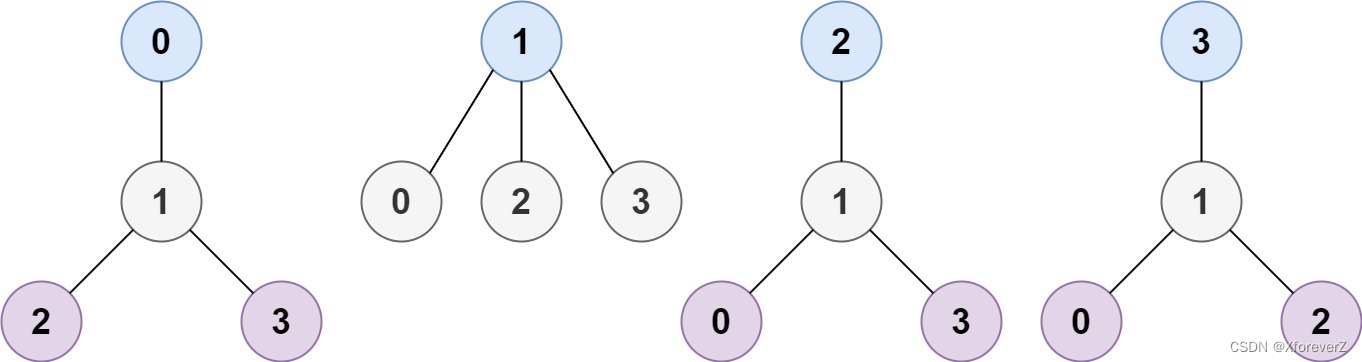
输入：n = 4, edges = [[1,0],[1,2],[1,3]]
输出：[1]
解释：如图所示，当根是标签为 1 的节点时，树的高度是 1 ，这是唯一的最小高度树。
示例 2：

输入：n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
输出：[3,4]

提示：

1 <= n <= 2 * 1e4
edges.length == n - 1
0 <= ai, bi < n
ai != bi
所有 (ai, bi) 互不相同
给定的输入保证是一棵树，并且不会有重复的边

没怎么了解过拓扑排序的题目，当然也可以用BFS或DFS做（虽然我没想出来orz）：

class Solution {
public:
    vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
        if (n == 1)
            return {0};
        vector<vector<int>> adj(n);
        vector<int> degree(n, 0);
        for (auto& edge : edges) {
            adj[edge[0]].push_back(edge[1]);
            adj[edge[1]].push_back(edge[0]);
            degree[edge[0]]++;
            degree[edge[1]]++;
        }
        queue<int> q;
        for (int i = 0; i < n; ++i) {
            if (degree[i] == 1)
                q.push(i);
        }
        while (n > 2) {
            int sz = q.size();
            n -= sz;
            for (int i = 0; i < sz; ++i) {
                int t = q.front();
                q.pop();
                for (auto& a : adj[t]) {
                    --degree[a];
                    if (degree[a] == 1)
                        q.push(a);
                }
            }
        }
        vector<int> res;
        while (!q.empty()) {
            res.push_back(q.front());
            q.pop();
        }
        return res;
    }
};

[303. 区域和检索 - 数组不可变](https://leetcode.cn/problems/range-sum-query-immutable/description/?envType=daily-question&envId=2024-03-18

给定一个整数数组 nums，处理以下类型的多个查询:

计算索引 left 和 right （包含 left 和 right）之间的 nums 元素的和，其中 left <= right
实现 NumArray 类：

NumArray(int[] nums) 使用数组 nums 初始化对象
int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的总和，包含 left 和 right 两点（也就是 nums[left] + nums[left + 1] + … + nums[right] )

示例 1：

输入：
[“NumArray”, “sumRange”, “sumRange”, “sumRange”]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出：
[null, 1, -1, -3]

解释：
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1))
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))

提示：

1 <= nums.length <= 1e4
-1e5 <= nums[i] <= 1e5
0 <= i <= j < nums.length
最多调用 1e4 次 sumRange 方法

经典前缀和：

class NumArray {
public:
    vector<int> preSum;

    NumArray(vector<int>& nums) {
        preSum.resize(nums.size() + 1, 0);
        for (int i = 0; i < nums.size(); ++i) {
            preSum[i + 1] = preSum[i] + nums[i];
        }
    }

    int sumRange(int i, int j) { return preSum[j + 1] - preSum[i]; }
};

1793. 好子数组的最大分数(Hard)

给你一个整数数组 nums （下标从 0 开始）和一个整数 k 。

一个子数组 (i, j) 的分数定义为 min(nums[i], nums[i+1], …, nums[j]) * (j - i + 1) 。一个好子数组的两个端点下标需要满足 i <= k <= j 。

请你返回好子数组的最大可能分数。

示例 1：

输入：nums = [1,4,3,7,4,5], k = 3
输出：15
解释：最优子数组的左右端点下标是 (1, 5) ，分数为 min(4,3,7,4,5) * (5-1+1) = 3 * 5 = 15 。
示例 2：

输入：nums = [5,5,4,5,4,1,1,1], k = 0
输出：20
解释：最优子数组的左右端点下标是 (0, 4) ，分数为 min(5,5,4,5,4) * (4-0+1) = 4 * 5 = 20 。

提示：

1 <= nums.length <= 1e5
1 <= nums[i] <= 2 * 1e4
0 <= k < nums.length

单调栈：

class Solution {
public:
    int maximumScore(vector<int>& nums, int k) {
        int n = nums.size();
        vector<int> left(n), right(n);
        stack<int> stk;
        for (int i = 0; i < n; ++i) {
            while (!stk.empty() && nums[stk.top()] >= nums[i]) {
                stk.pop();
            }
            left[i] = stk.empty() ? -1 : stk.top();
            stk.push(i);
        }
        while (!stk.empty()) {
            stk.pop();
        }
        for (int i = n - 1; i >= 0; --i) {
            while (!stk.empty() && nums[stk.top()] >= nums[i]) {
                stk.pop();
            }
            right[i] = stk.empty() ? n : stk.top();
            stk.push(i);
        }
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            if (left[i] < k && k < right[i]) {
                ans = max(ans, nums[i] * (right[i] - left[i] - 1));
            }
        }
        return ans;
    }
};