目录
332.重新安排行程
思路:
51. N皇后
思路:
37. 解数独
332.重新安排行程
力扣题目链接
(opens new window)
给定一个机票的字符串二维数组 [from, to],子数组中的两个成员分别表示飞机出发和降落的机场地点,对该行程进行重新规划排序。所有这些机票都属于一个从 JFK(肯尼迪国际机场)出发的先生,所以该行程必须从 JFK 开始。
提示:
- 如果存在多种有效的行程,请你按字符自然排序返回最小的行程组合。例如,行程 ["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小,排序更靠前
- 所有的机场都用三个大写字母表示(机场代码)。
- 假定所有机票至少存在一种合理的行程。
- 所有的机票必须都用一次 且 只能用一次。
示例 1:
- 输入:[["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
- 输出:["JFK", "MUC", "LHR", "SFO", "SJC"]
示例 2:
- 输入:[["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
- 输出:["JFK","ATL","JFK","SFO","ATL","SFO"]
- 解释:另一种有效的行程是 ["JFK","SFO","ATL","JFK","ATL","SFO"]。但是它自然排序更大更靠后。
思路:这道题目有几个难点:
- 一个行程中,如果航班处理不好容易变成一个圈,成为死循环
- 有多种解法,字母序靠前排在前面,让很多同学望而退步,如何该记录映射关系呢 ?
- 使用回溯法(也可以说深搜) 的话,那么终止条件是什么呢?
- 搜索的过程中,如何遍历一个机场所对应的所有机场。
如何该记录映射关系呢 ?
一个机场映射多个机场,机场之间要靠字母序排列,一个机场映射多个机场,可以使用std::unordered_map,如果让多个机场之间再有顺序的话,就是用std::map 或者std::multimap 或者 std::multiset。
这样存放映射关系可以定义为
unordered_map<string, multiset<string>> targets或者unordered_map<string, map<string, int>> targets含义如下:
unordered_map<string, multiset> targets:unordered_map<出发机场, 到达机场的集合> targets
unordered_map<string, map<string, int>> targets:unordered_map<出发机场, map<到达机场, 航班次数>> targets
这两个结构,我选择了后者,因为如果使用
unordered_map<string, multiset<string>> targets遍历multiset的时候,不能删除元素,一旦删除元素,迭代器就失效了。所以搜索的过程中就是要不断的删multiset里的元素,那么推荐使用
unordered_map<string, map<string, int>> targets。在遍历
unordered_map<出发机场, map<到达机场, 航班次数>> targets的过程中,可以使用"航班次数"这个字段的数字做相应的增减,来标记到达机场是否使用过了。如果“航班次数”大于零,说明目的地还可以飞,如果“航班次数”等于零说明目的地不能飞了,而不用对集合做删除元素或者增加元素的操作。
相当于说我不删,我就做一个标记
class Solution {
public:
//unordered_map<出发机场, map<到达机场,航班次数>>targets;
unordered_map<string, map<string,int>>targets;
bool backtracking(int ticketNum,vector<string>& result){
if(result.size()==ticketNum+1){
return true;
}
for(pair<const string,int>&target:targets[result[result.size()-1]]){
if(target.second>0){//记录飞机是否到过
result.push_back(target.first);
target.second--;
if(backtracking(ticketNum,result))return true;
target.second++;
result.pop_back();
}
}
return false;
}
vector<string> findItinerary(vector<vector<string>>& tickets) {
targets.clear();
vector<string>result;
for(const vector<string>& vec:tickets){
targets[vec[0]][vec[1]]++;//记录映射关系
}
result.push_back("JFK");//开始机场
backtracking(tickets.size(),result);
return result;
}
};51. N皇后
力扣题目链接
(opens new window)
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
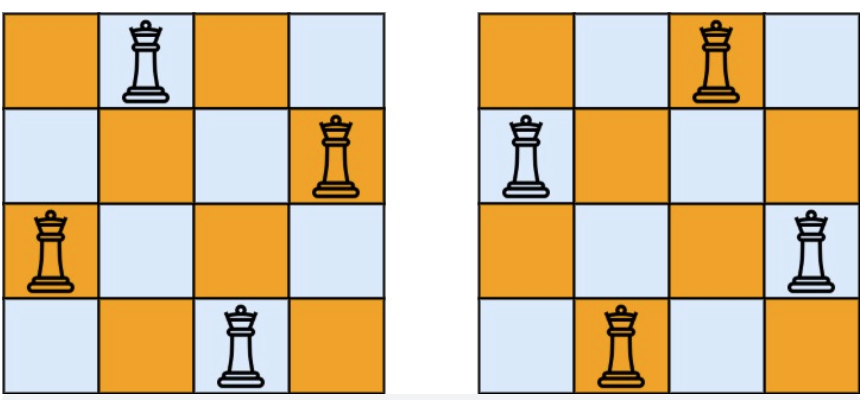
- 输入:n = 4
- 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
- 解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
- 输入:n = 1
- 输出:[["Q"]]
思路:先来看一下皇后们的约束条件:
- 不能同行
- 不能同列
- 不能同斜线
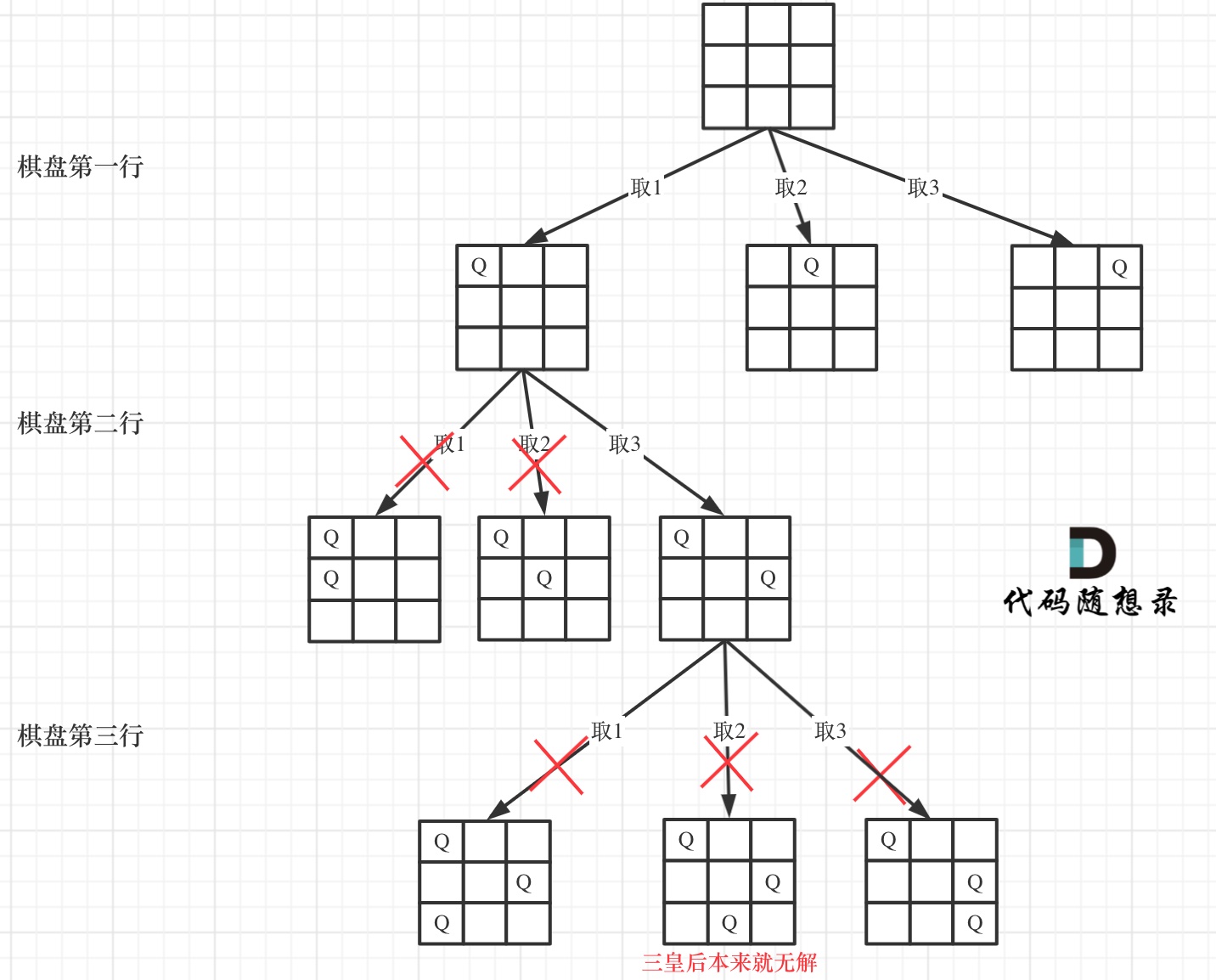
确定完约束条件,来看看究竟要怎么去搜索皇后们的位置,其实搜索皇后的位置,可以抽象为一棵树。
下面我用一个 3 * 3 的棋盘,将搜索过程抽象为一棵树,如图:
从图中,可以看出,二维矩阵中矩阵的高就是这棵树的高度,矩阵的宽就是树形结构中每一个节点的宽度。
那么我们用皇后们的约束条件,来回溯搜索这棵树,只要搜索到了树的叶子节点,说明就找到了皇后们的合理位置了
递归深度就是row控制棋盘的行,每一层里for循环的col控制棋盘的列,一行一列,确定了放置皇后的位置。
每次都是要从新的一行的起始位置开始搜,所以都是从0开始。
可以看出,当递归到棋盘最底层(也就是叶子节点)的时候,就可以收集结果并返回了。
class Solution {
public:
vector<vector<string>>result;
void backtracking(int n, int row, vector<string>& chessboard){
if(row==n){
result.push_back(chessboard);
return;
}
for(int col=0;col<n;col++){//横向遍历,遍历列
if(isValid(row, col, chessboard, n)){
chessboard[row][col]='Q';
backtracking(n, row+1, chessboard);//纵向遍历,遍历行
chessboard[row][col]='.';//回溯
}
}
}
bool isValid(int row, int col, vector<string>& chessboard, int n){
//检查列
for(int i=0; i<row;i++){
if(chessboard[i][col]=='Q')return false;
}
//检查45度
for(int i=row-1,j=col-1;i>=0&&j>=0;i--,j--){
if(chessboard[i][j]=='Q')return false;
}
//检查135度
for(int i=row-1,j=col+1; i>=0&&j<n;i--,j++){
if(chessboard[i][j]=='Q')return false;
}
return true;
}
vector<vector<string>> solveNQueens(int n) {
result.clear();
vector<string>chessboard(n,string(n,'.'));
backtracking(n,0,chessboard);
return result;
}
};37. 解数独
力扣题目链接
(opens new window)
编写一个程序,通过填充空格来解决数独问题。
一个数独的解法需遵循如下规则: 数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。 空白格用 '.' 表示。
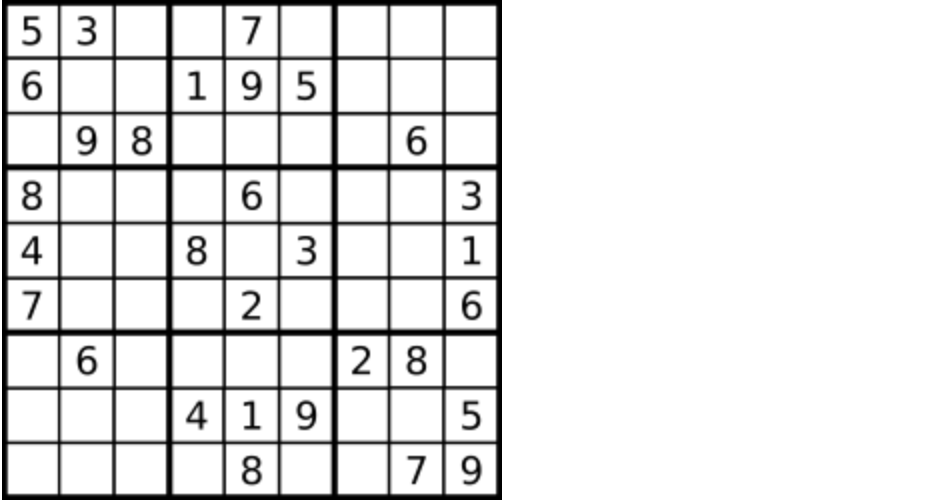
一个数独。
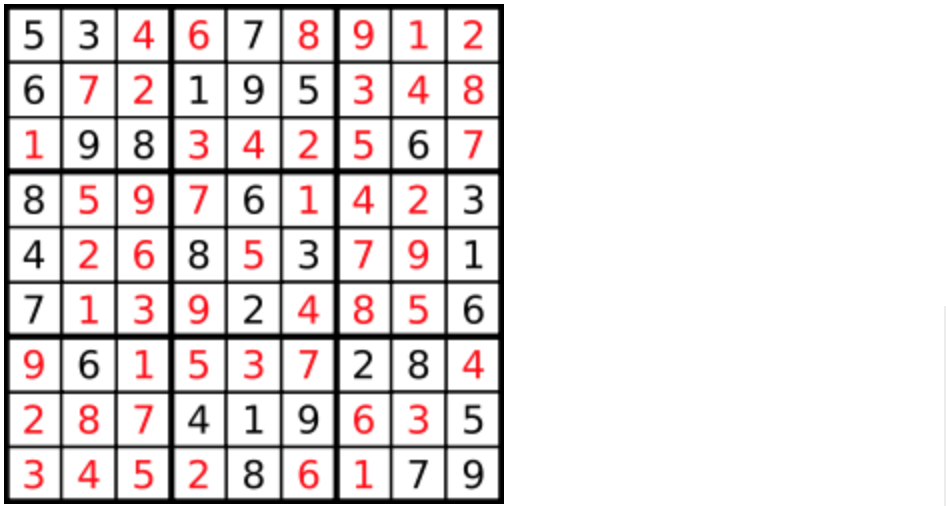
答案被标成红色。
提示:
- 给定的数独序列只包含数字 1-9 和字符 '.' 。
- 你可以假设给定的数独只有唯一解。
- 给定数独永远是 9x9 形式的
思路:
N皇后问题
(opens new window)是因为每一行每一列只放一个皇后,只需要一层for循环遍历一行,递归来遍历列,然后一行一列确定皇后的唯一位置。
本题就不一样了,本题中棋盘的每一个位置都要放一个数字(而N皇后是一行只放一个皇后),并检查数字是否合法,解数独的树形结构要比N皇后更宽更深。
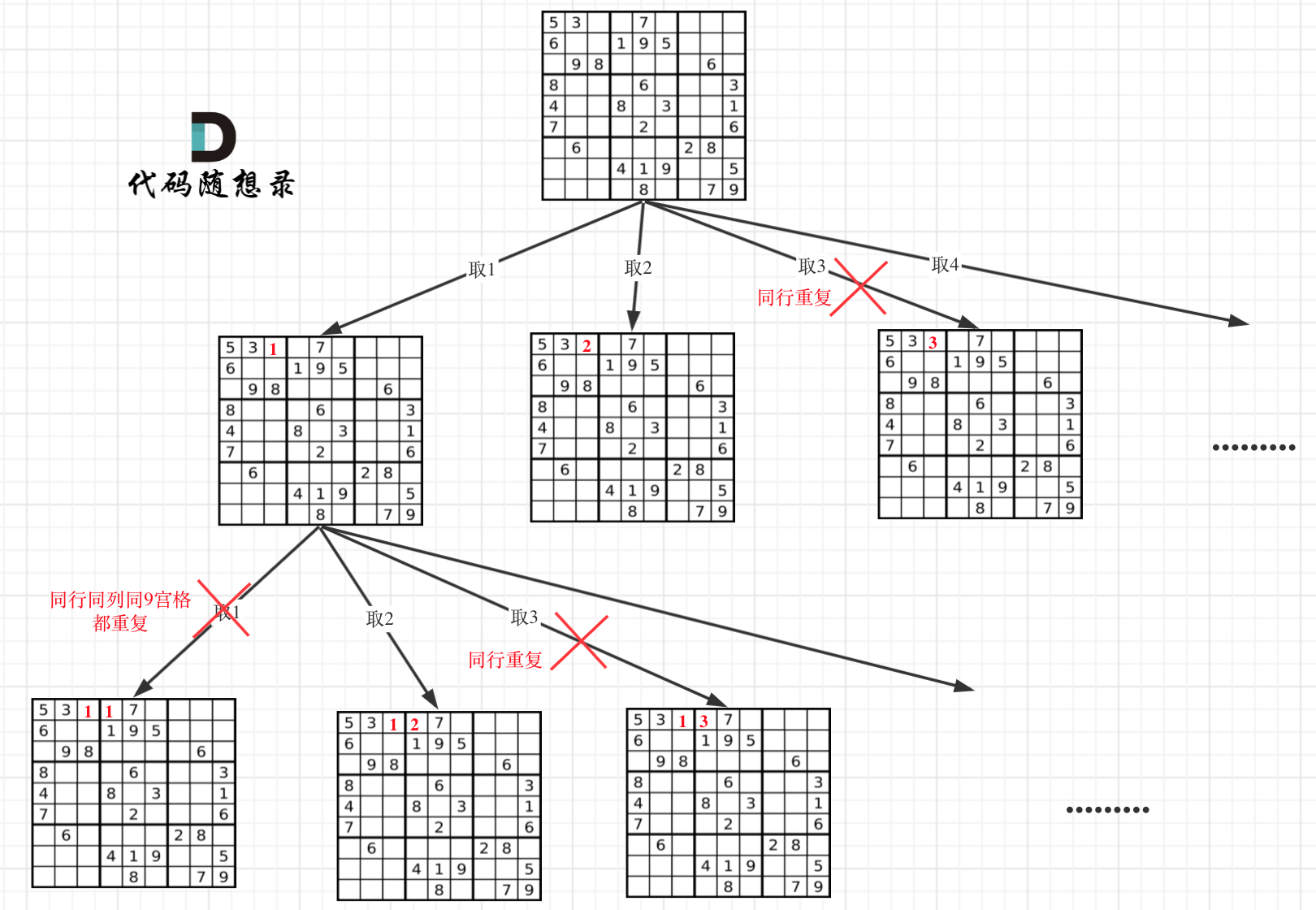
因为这个树形结构太大了,我抽取一部分,如图所示:
在树形图中可以看出我们需要的是一个二维的递归(也就是两个for循环嵌套着递归)
一个for循环遍历棋盘的行,一个for循环遍历棋盘的列,一行一列确定下来之后,递归遍历这个位置放9个数字的可能性!
判断棋盘是否合法有如下三个维度:
- 同行是否重复
- 同列是否重复
- 9宫格里是否重复
class Solution {
public:
bool backtracking(vector<vector<char>>& board){
for(int i=0;i<board.size();i++){//遍历行
for(int j=0;j<board[0].size();j++){//遍历列
//遍历1-9看看是否能放在这里
if(board[i][j]=='.'){
for(char k='1';k<='9';k++){
if(isValid(i,j,k,board)){
board[i][j]=k;
if(backtracking(board))return true;
board[i][j]='.';//回溯
}
}
return false;//1-9都不合适,放置失败
}
}
}
return true;
}
bool isValid(int row, int col, int val, vector<vector<char>>& board){
//检查行
for(int i=0;i<9;i++){
if(board[row][i]==val)return false;
}
//检查列
for(int j=0;j<9;j++){
if(board[j][col]==val)return false;
}
//检查3*3九宫格
int startRow=(row/3)*3;
int startCol=(col/3)*3;
for(int i=startRow;i<startRow+3;i++){
for(int j=startCol;j<startCol+3;j++){
if(board[i][j]==val)return false;
}
}
return true;
}
void solveSudoku(vector<vector<char>>& board) {
backtracking(board);
}
};参考:代码随想录