文章目录
- 📝前言
- 🌠 创建简单二叉树
- 🌉二叉树的三种遍历
- 🌠前序
- 🌉中序遍历
- 🌠后序遍历
- 🌠二叉树节点个数
- 🌉二叉树节点个数注意点
- 🚩总结
📝前言
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
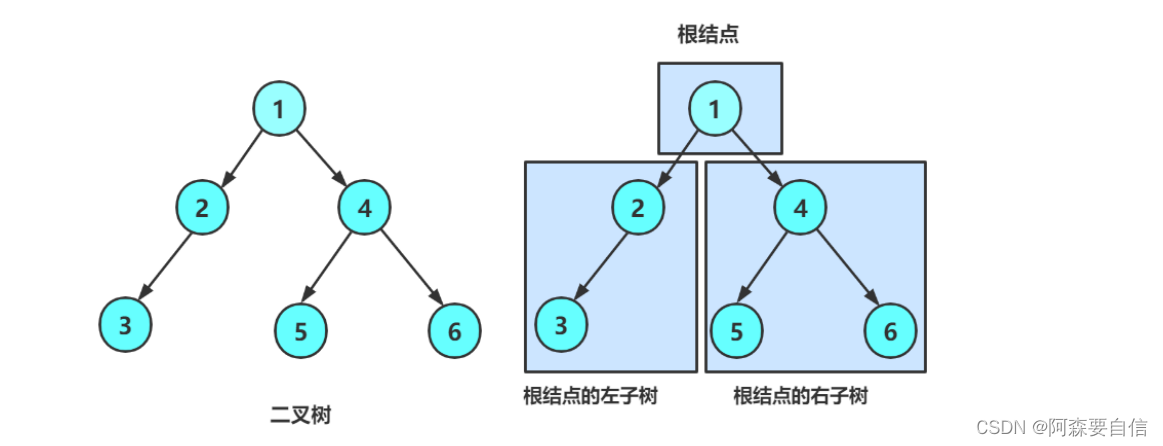
二叉树可以没有节点(空树)否则,它包含一个根节点,这个根节点最多可以有两个分支:左子树和右子树,左右子树也符合二叉树的定义,可以是空树,或者由根节点和其左右子树组成。
因此二叉树的定义采用的是递归的思想:一个二叉树要么为空,要么由根节点和其左右两个子二叉树组成。左右子树本身也符合二叉树的定义,可以递归定义下去。
本小节我们将学习二叉树的前中后序遍历!
🌠 创建简单二叉树
在学习二叉树的基本操作之前,需要先创建一棵二叉树,然后才能学习相关的基本操作。由于现在大家对二叉树结构的理解还不够深入,为了降低学习成本,这里手动快速创建一棵简单的二叉树,以便快速进入二叉树操作学习。等大家对二叉树结构有了一定了解之后,再深入研究二叉树的真正创建方式。
手插简单二叉树代码:
// 二叉树节点结构体定义
typedef struct BinTreeNode
{
// 左子节点指针
struct BinTreeNode* left;
// 右子节点指针
struct BinTreeNode* right;
// 节点值
int val;
}BTNode;
// 创建节点,分配内存并返回
BTNode* BuyBTNode(int val)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
// 空间分配失败
if (newnode == NULL)
{
perror("malloc fail");
return NULL;
}
// 初始化节点值
newnode->val = val;
// 初始化左右子节点为NULL
newnode->left = NULL;
newnode->right = NULL;
return newnode;
}
// 创建示例树
BTNode* CreateTree()
{
// 创建节点1-6
BTNode* n1 = BuyBTNode(1);
BTNode* n2 = BuyBTNode(2);
BTNode* n3 = BuyBTNode(3);
BTNode* n4 = BuyBTNode(4);
BTNode* n5 = BuyBTNode(5);
BTNode* n6 = BuyBTNode(6);
// 构建树结构
n1->left = n2;
n1->right = n4;
n2->left = n3;
n4->left = n5;
n4->right = n6;
return n1; // 返回根节点
}
二叉树的图像:
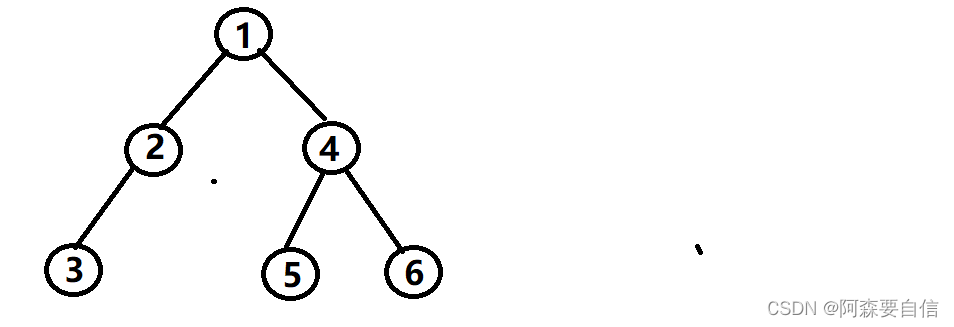
注意:上述代码并不是创建二叉树的方式,真正创建二叉树方式后序详解重点讲解。
🌉二叉树的三种遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
🌠前序
您说得对,我来补充一下前序遍历的注释:
前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
算法:
访问根节点 -> 前序遍历左子树 -> 前序遍历右子树
- 即先访问根节点,然后遍历其左子树,再遍历其右子树。
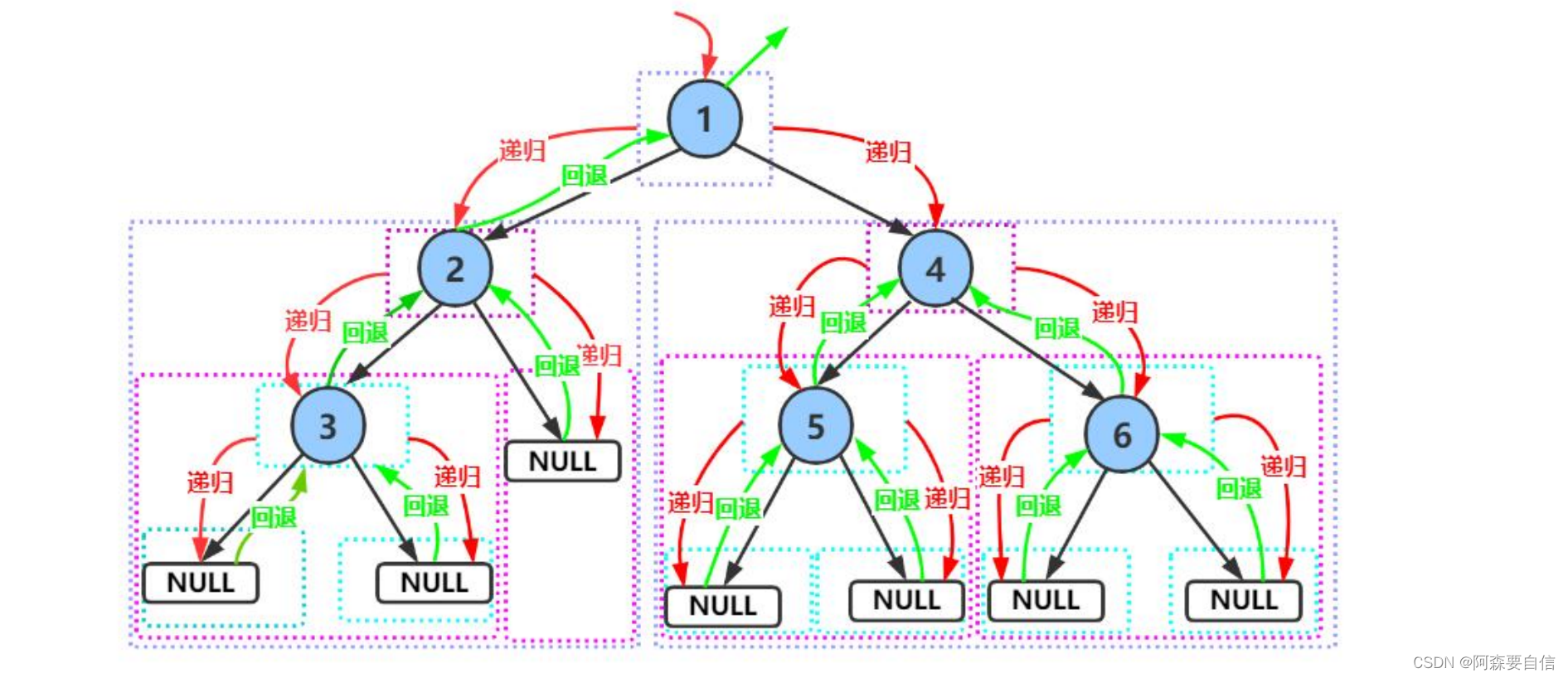
注意:
递归基准条件是当根节点为NULL时返回。访问根节点要放在递归左右子树之前,这保证了根节点一定先于其子节点被访问。递归左子树和右子树的顺序不能调换,否则就不是前序遍历了。
代码:
void PreOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
printf("%d ", root->val);
PreOrder(root->left);
PreOrder(root->right);
}
int main()
{
BTNode* root = CreateTree();
PreOrder(root);
printf("\n");
}
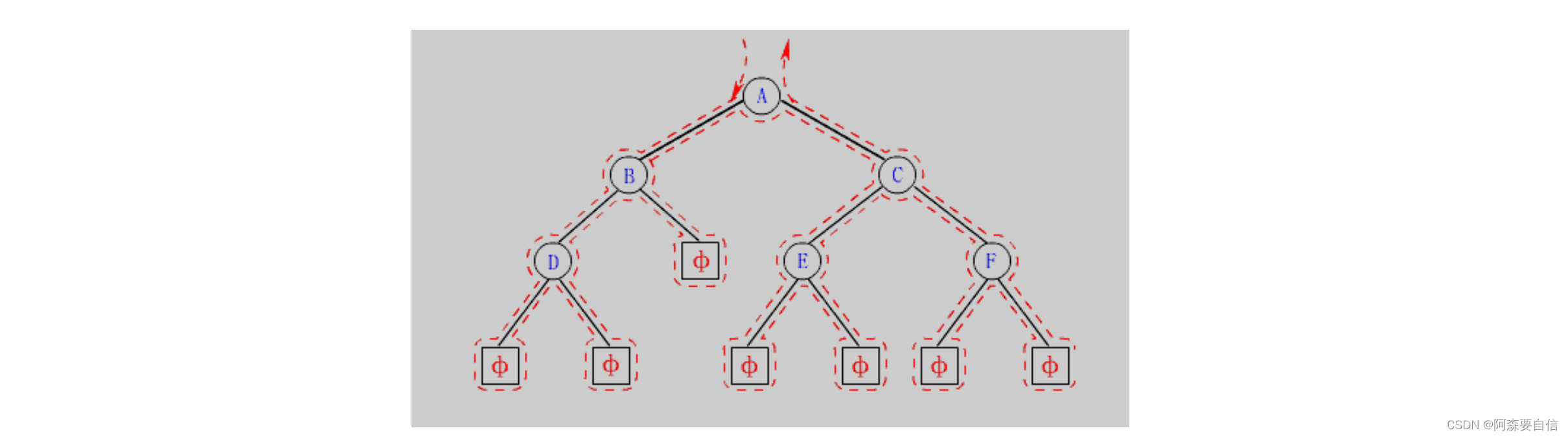
前序递归图解:
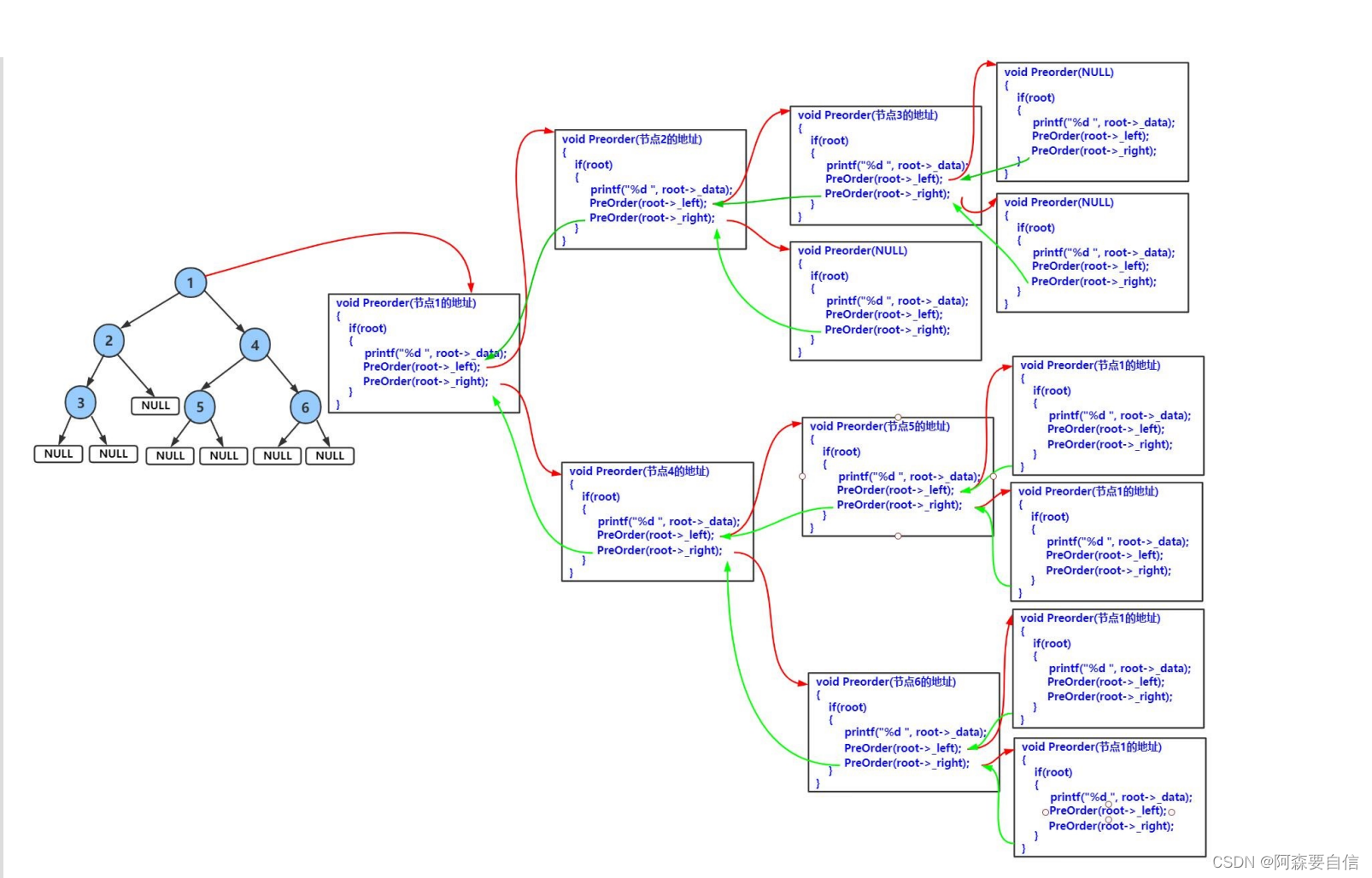
运行:
🌉中序遍历
中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。中序遍历是在遍历一个结点的左子树后,然后访问这个结点,最后遍历它的右子树。
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
InOrder(root->left);
printf("%d ", root->val);
InOrder(root->right);
}

🌠后序遍历
后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
后序遍历是先遍历一个结点的左右子树,最后再访问这个结点。
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->val);
}
后序运行图:

由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。

🌠二叉树节点个数
这里分别实现前序、中序和后序遍历方式统计二叉树节点个数:
前序遍历:
int PreOrderCount(BTNode* root)
{
if(root == NULL) return 0;
count++;
PreOrderCount(root->left);
PreOrderCount(root->right);
return count;
}
int TreeSize(BTNode* root)
{
if(root == NULL) return 0;
count = 0;
PreOrderCount(root);
return count;
}
中序遍历:
int InOrderCount(BTNode* root)
{
if(root == NULL) return 0;
InOrderCount(root->left);
count++;
InOrderCount(root->right);
return count;
}
int TreeSize(BTNode* root)
{
if(root == NULL) return 0;
count = 0;
InOrderCount(root);
return count;
}
后序遍历:
int PostOrderCount(BTNode* root)
{
if(root == NULL) return 0;
PostOrderCount(root->left);
PostOrderCount(root->right);
count++;
return count;
}
int TreeSize(BTNode* root)
{
if(root == NULL) return 0;
count = 0;
PostOrderCount(root);
return count;
}
三种遍历方式都是通过递归遍历每个节点,并在遍历每个节点时将统计变量count加1,最终count的值即为树的节点总数。
🌉二叉树节点个数注意点
注意当我们TreeSize函数使用了static变量size来统计节点个数,static变量的值会在函数调用之间保留,所以第二次调用TreeSize时,size的值会继续增加,导致统计结果叠加。
int TreeSize(BTNode* root)
{
static int size = 0;
if (root == NULL)
return 0;
else
++size;
TreeSize(root->left);
TreeSize(root->right);
return size;
}
int main()
{
printf("TreeSize : %d\n", TreeSize(root));
printf("TreeSize : %d\n", TreeSize(root));
}
代码运行:

改进
为了解决使用static变量导致的结果叠加问题,可以考虑使用以下方法:
- 每次调用TreeSize前重置size为0:
int TreeSize(BTNode* root) {
static int size = 0;
size = 0;
// reset size
if (root == NULL)
return 0;
else
++size;
TreeSize(root->left);
TreeSize(root->right);
return size;
}
- 不使用static变量,直接返回递归调用的结果:
int TreeSize(BTNode* root)
{
if (root == NULL)
return 0;
else
return 1 + TreeSize(root->left) + TreeSize(root->right);
}
如果当前节点为NULL,直接返回0否则,返回:当前节点本身为1,加上左子树的节点数(TreeSize(root->left)返回值),加上右子树的节点数(TreeSize(root->right)返回值)
- 将size定义为函数参数,每次递归传递:
int TreeSize(BTNode* root, int* size)
{
if (root == NULL)
return 0;
*size += 1;
TreeSize(root->left, size);
TreeSize(root->right, size);
return *size;
}
int main()
{
// 调用
int size = 0;
TreeSize(root, &size);
}
🚩总结