在旋转点,旋转矩阵的逆等于矩阵的转置

视图变换和投影变换

三维变换

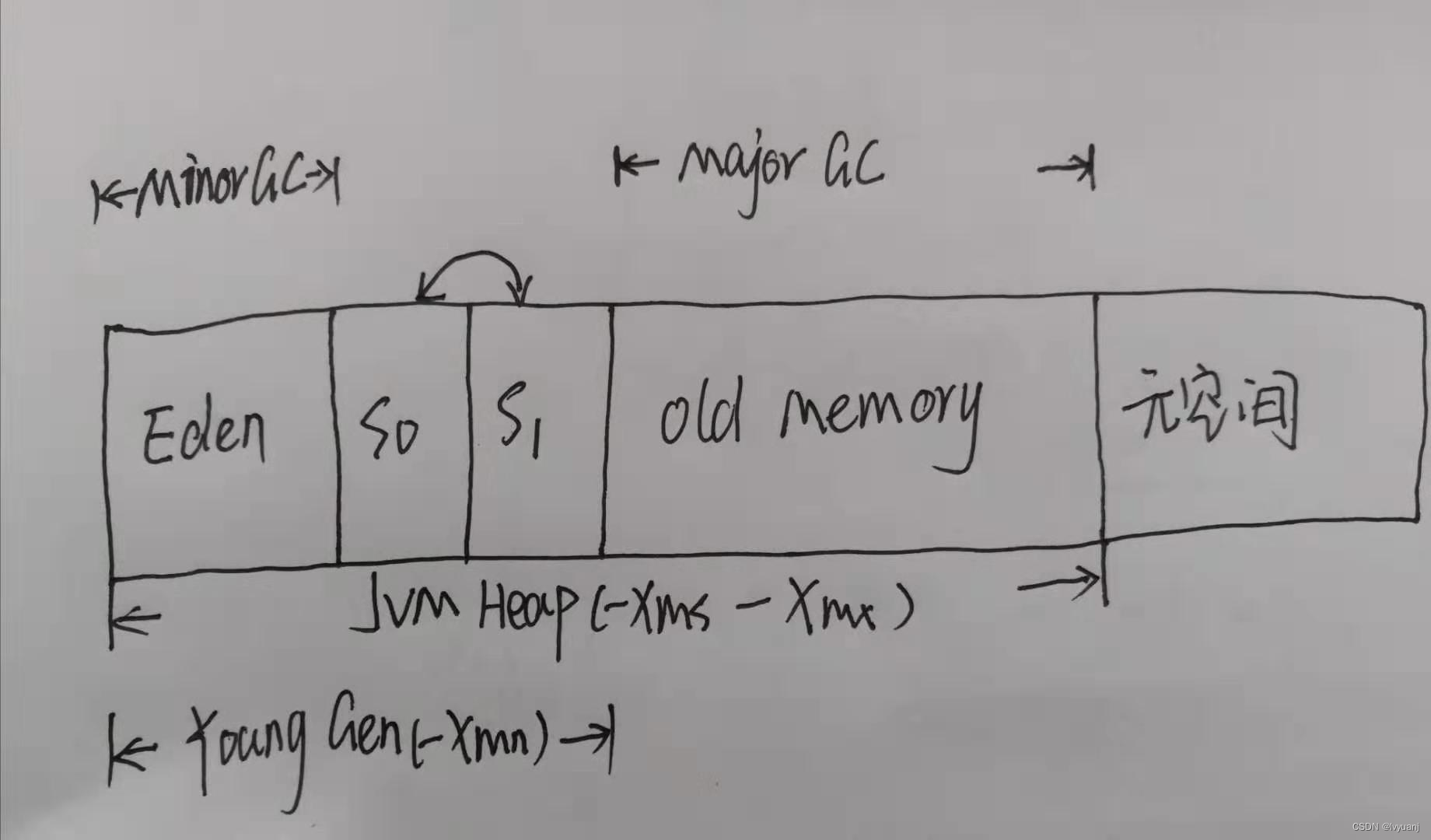
左边3*3是线性变换,右边一列是仿射变换(平移)

先线性再平移
缩放、旋转、平移


x叉乘y得到z,y叉乘z得到x, xyz给任何两个可以得到另一个
(循环对称) z叉乘x得到y,所以y是反的
3D旋转

任意绕3d轴旋转可以分解为绕x,y,z轴旋转。三个角为欧拉角
罗德里格斯旋转公式
绕n单位向量方向旋转α角。
推导过程

N的矩阵和把叉乘转成矩阵时的矩阵是一样的
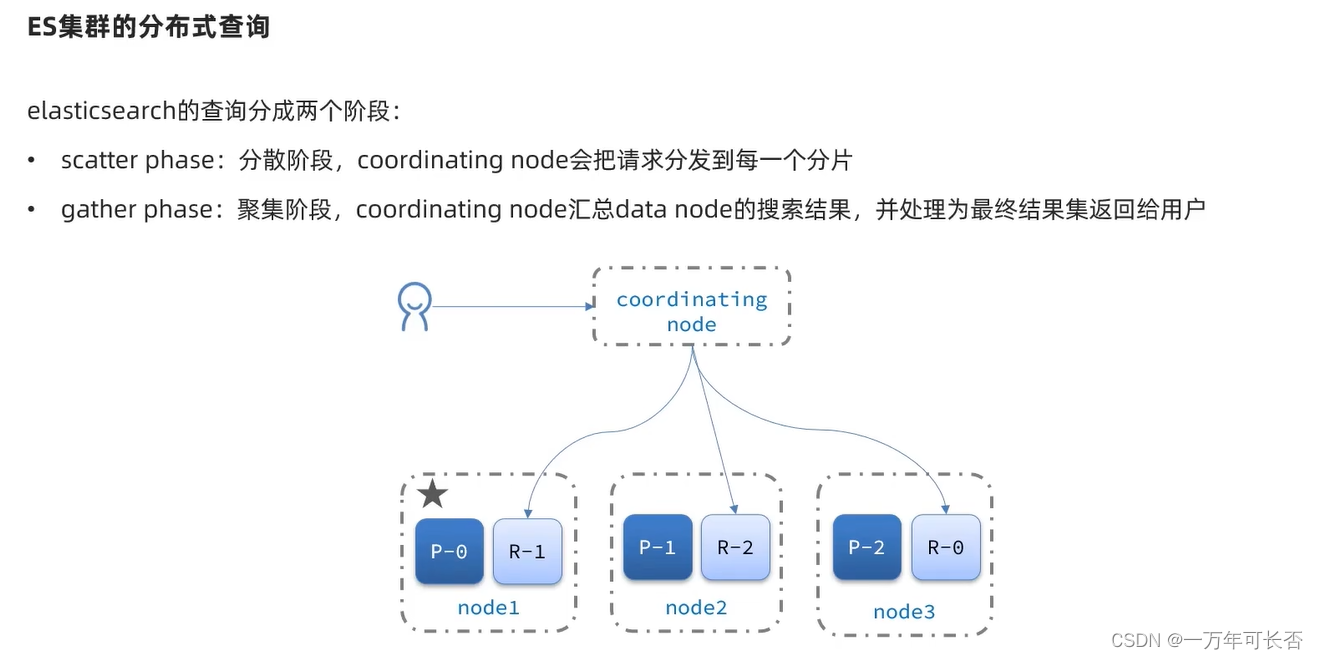
View/Camera Transformation
MVP变换:
拍照:
找一个位置,人站好。相当于模型变换
找一个好的角度放相机。相当于视图变换
拍照。相当于投影变换

相机的位置,相机的朝向,定义相机向上的方向

相机默认放在原点,朝向-z,向上为y

从e平移到原点,把观察轴g旋转成-z,旋转t到y,g*t自然就是x轴方向

原始旋转Rview不好求,可以反过来求从原点旋转到相机角度,即x旋转到g叉乘t,y旋转到t,z旋转到-g
==>> (1,0,0)转到
(
x
g
×
t
,
y
g
×
t
,
z
g
×
t
)
(x_{g{\times}t},y_{g{\times}t},z_{g{\times}t})
(xg×t,yg×t,zg×t), (0,1,0)转到
(
x
t
,
y
t
,
z
t
)
(x_t,y_t,z_t)
(xt,yt,zt), (0,0,1)转到
(
x
−
g
,
y
−
g
,
z
−
g
)
(x_{-g},y_{-g},z_{-g})
(x−g,y−g,z−g)
==>>
R
v
i
e
w
−
1
⋅
(
0
,
1
,
0
)
=
(
x
t
,
y
t
,
z
t
)
R^{-1}_{view} · (0,1,0) = (x_t,y_t,z_t)
Rview−1⋅(0,1,0)=(xt,yt,zt)
==>> 矩阵中间一列是
[
x
t
,
y
t
,
z
t
]
[x_t,y_t, z_t]
[xt,yt,zt]
再做逆变换 (旋转矩阵是正交矩阵,所以旋转矩阵求逆等于将其转置)
逆矩阵:矩阵的逆是指对于一个可逆矩阵 A,存在一个矩阵 B,使得 A 乘以 B 等于单位矩阵。B为A的逆矩阵
转置矩阵:将矩阵的行和列互换得到的新矩阵
如果是反向旋转一个角度,最终得到的旋转矩阵其实是正向旋转矩阵的 逆矩阵 ,由于这个矩阵是正交阵 ,所以逆矩阵就是转置矩阵
总结:物体和相机做一样的变换,相机变换到原点,向上为y,朝向-z。即模型视图变换(ModelView Transformation)
Projection transformation

正交投影:不会有近大远小的现象
透视投影

正交投影相当于相机离的无限远,则近平面与远平面几乎一样大小
正交投影

相机归位原点后,扔掉z坐标,不管x,y范围多到,转换到[-1,1], 得到的结果就是正交投影

定义空间中的一个立方体(空间中要做正交投影的范围),定义立方体的左右在x轴上是多少,下上在y轴是多少,远近在z轴是多少。将立方体映射到标准立方体[-1,1]
如何映射:把立方体的中心移到原点,把xyz轴分别拉成 -1到1。
f、n代表了远近,越远,z值越小,即 n > f。因为是沿着-z方向。为了保证右手坐标系。
在一些api如openGL等是左手系,但是x叉乘y不再等于z

先平移再缩放
透视变换

近大远小,平行线不再平行,相较于一点

(1,0,0,1)和(2,0,0,2)在3D里代表同一个点

从一个点往外看,同样定义一个近平面和远平面。
先将远平面的4个点挤到近平面,再做正交投影
注意:
- 近平面永远不变
- 挤完之后,远平面z值不变
- 挤完之后,中心点仍为中心


从透视到正交:从侧面看,是相似三角形。求出远平面的y点在近平面的y点,x同理。
根据齐次坐标都乘以z

注意第4行是(0,0,1,0)而不是(0,0,0,z)因为z不是常量

任何一个点在近平面都不变,任何点在近平面和远平面的z值不变,近平面的z值定义为n
近平面的(x,y,n,1)经过0000投影变换仍是(x,y,n,1)

远平面的中心点经过变换仍是中心点,远平面的z值为f
远平面的(0,0,f,1)经过投影变换仍是(0,0,f,1)

透视矩阵的参数:
fov:视场角
aspect:宽高比
far:远平面
near:近平面
提问/作业
问题:对于中间的任何一个点,某一个z,如 z =
n
+
f
2
{n+f}\over{2}
2n+f,经过变换后,z会如何变换。是变大(更接近于n)还是变小(更接近于f):
x,y影响忽略,带入(0,0,
n
+
f
2
{n+f}\over{2}
2n+f, 1)到投影变换方程
==>> (0,0,
n
2
+
f
2
2
{n^2+f^2}\over{2}
2n2+f2,
n
+
f
2
{n+f}\over{2}
2n+f)
==>> (0,0,
n
2
+
f
2
n
+
f
{n^2+f^2}\over{n+f}
n+fn2+f2, 1)
==>>
n
2
+
f
2
n
+
f
{n^2+f^2}\over{n+f}
n+fn2+f2 -
n
+
f
2
{n+f}\over{2}
2n+f
==>>
(
n
−
f
)
2
2
(
n
+
f
)
{(n-f)^2}\over{2(n+f)}
2(n+f)(n−f)2
==>> 镜头朝向-z,分母为负,分子为正。 小于0
==>>变换后的z值小于变换前的z值,更接近与远平面
==>>近大远小
显示三角形并控制旋转

绕任一向量旋转
绕(1,1,-1)

github 作业地址



![flask之ssti [WesternCTF2018]shrine1](https://img-blog.csdnimg.cn/direct/9db481941a844b6da32e8093be44f411.png)