1、嵌套循环时间复杂度的计算

该程序，最上面的嵌套循环里，i每执行一次，j就执行N次，所以嵌套循环执行次数为N*N次；中间的k变量循环了2*N次；最后M变量循环10次。所以总共执行了 N*N+2*N+10 次！

所以该程序时间复杂度为O(N²) 。

2、双重循环时间复杂度的计算

该程序，上面的for循环执行了2*N次，下面的M循环了10次。所以该时间复杂度的函数式为 F(N)=2N+10。则时间复杂度为O(N)。

该程序，上面的循环了M次，下面循环了N次，所以该时间复杂度为O(M+N)。

3、常数循环时间复杂度的计算

该程序执行了100次，因为没有未知数是常数次，所以该程序的时间复杂度为O(1)。注意不是代表算法运行一次，运行的是常数次。

4、strchr时间复杂度的计算

strchr的功能是查找字符，程序大致如下：

我们假设从hello world中去查找字符，那么

所以我们认为该时间复杂度为最坏情况O(N)。

5、冒泡排序的时间复杂度计算

冒泡排序的执行次数是(N-1)+(N-2)+…+1次。

举个例子来说，一个数列 5 4 3 2 1 进行冒泡升序排列，第一次大循环从第一个数（5）开始到倒数第二个数（2）结束。
比较过程：先比较5和4，4比5小，交换位置变成4 5 3 2 1，比较5和3，3比5小，交换位置变成4 3 5 2 1……最后比较5和1，1比5小，交换位置变成4 3 2 1 5，这时候共进行了4次比较交换运算，最后1个数变成了数列最大数。

对于n位的数列则有比较次数为 (n-1) + (n-2) + …… + 1 = n * (n - 1) / 2，也就是等差数列求和，这就得到了最大的比较次数。
将n * (n - 1) / 2展开得到的最大量级为n²。所以冒泡排序的时间复杂度为O(n²)。

6、二分查找的时间复杂度计算

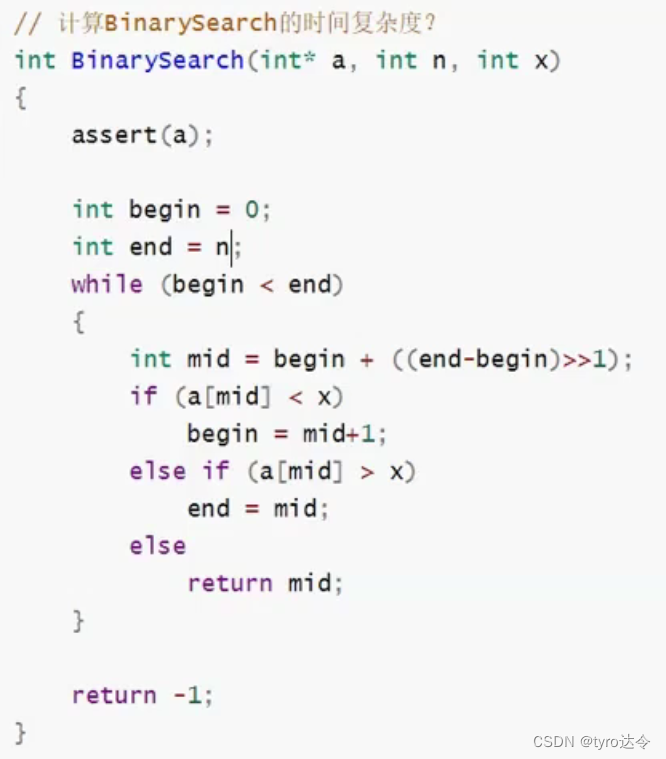
算时间复杂度不能只是去看几层循环，而是要去看它的思想。
此处，二分查找每查找一次就要除以2。假设一个数组大小为N，那么每查找一次，N就要除以2，最好的情况是O(1)，最坏的情况是查找到最后N/2/2/…/2=1,也就是2^x=N，所以X=log2N

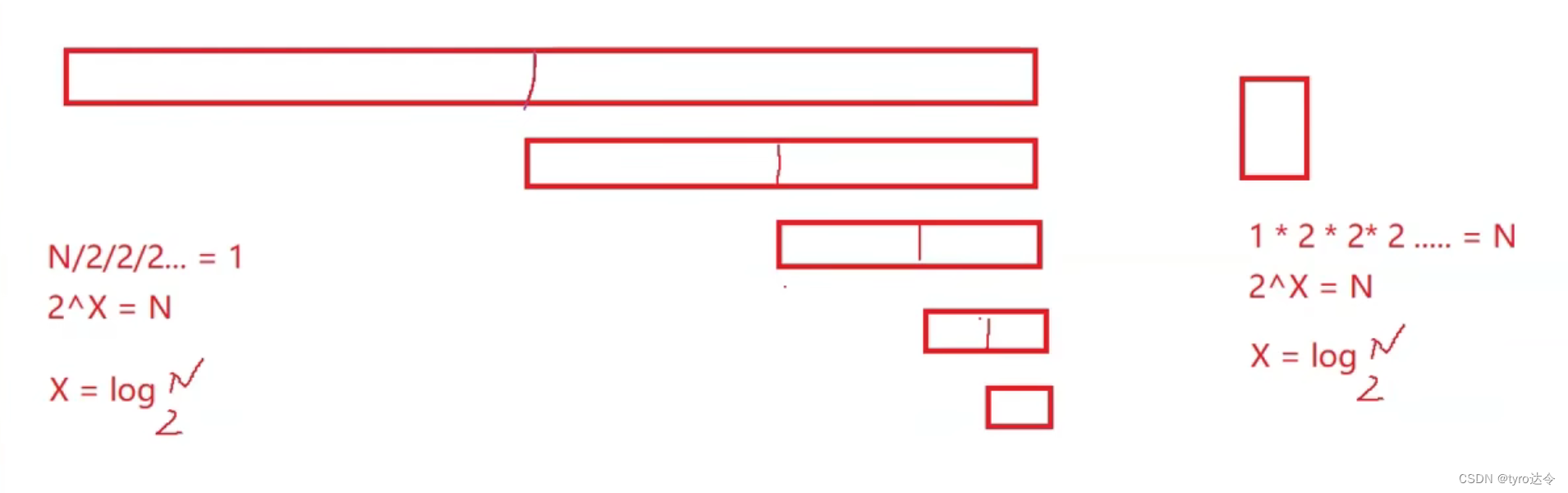
所以是二分查找时间复杂度为

7、计算n的阶乘递归时间复杂度计算

递归算法：递归次数*每次递归调用的次数。
这里递归了N次，而每次调用的次数为常数次，所以可忽略，则该时间复杂度为O(N)。

8、斐波那契的时间复杂度计算

这里也可用递归算法求，也就是递归次数*每次递归调用的次数。

递归次数为2⁰+2¹+…+2^n-1，而每次递归调用的次数为常数次可忽略不计。所以可看成等比数列求和。

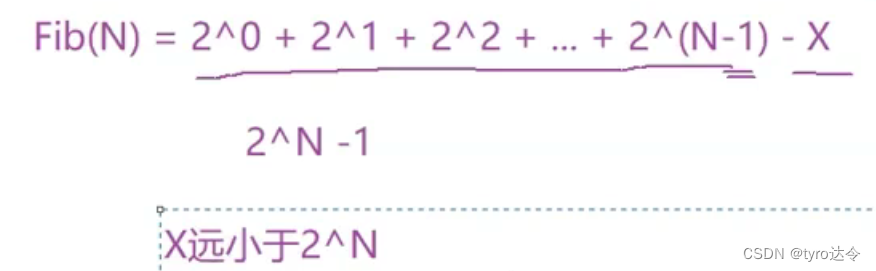
所以该时间复杂度为O(2^N)。

最后总结，我们计算时间复杂度不能单纯只看执行次数，最好是画图自己理解计算，利用公式等来求我们的时间复杂度。