概述

求一个点沿任意直线对称的点的坐标，这是一个简单的初中几何问题，如果用传统的求解思路，就是用公式，解方程组。但是作为Godot的使用者，要深谙向量的魅力。
我们绘制如下的图来分析：

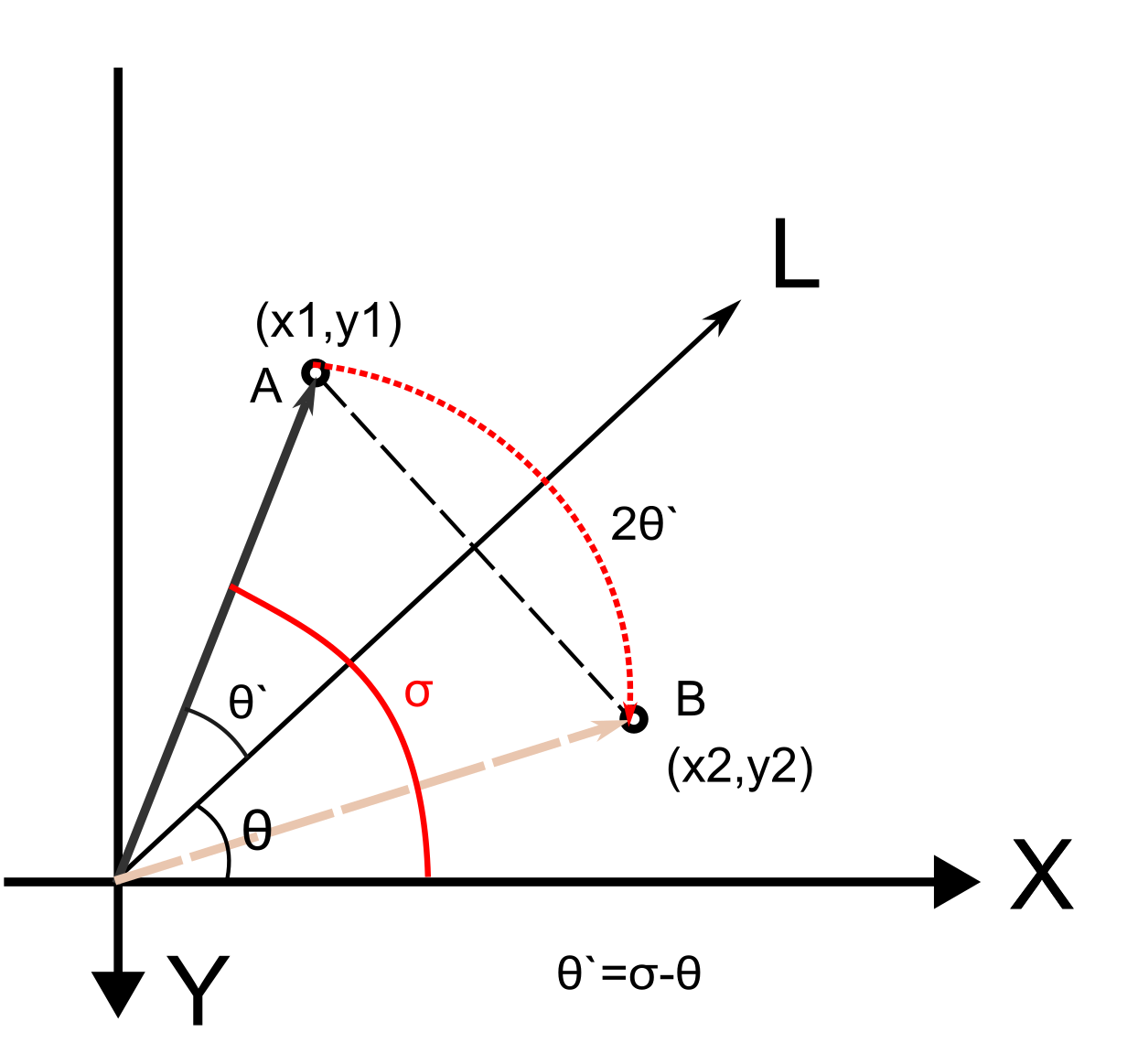
• 对称轴L可以被理解为一个向量
• A点也可以理解为一个从坐标系原点指向(x1,y1)的向量
• A向量与X轴的夹角为σ
• L向量与X轴的夹角为θ
• 则A向量与对称轴L向量的夹角θ'=σ-θ
• 那么B点坐标就可以通过A向量旋转2θ'求得。
• 如果L不经过原点，那么只需要加上偏移值offset就可以了

测试

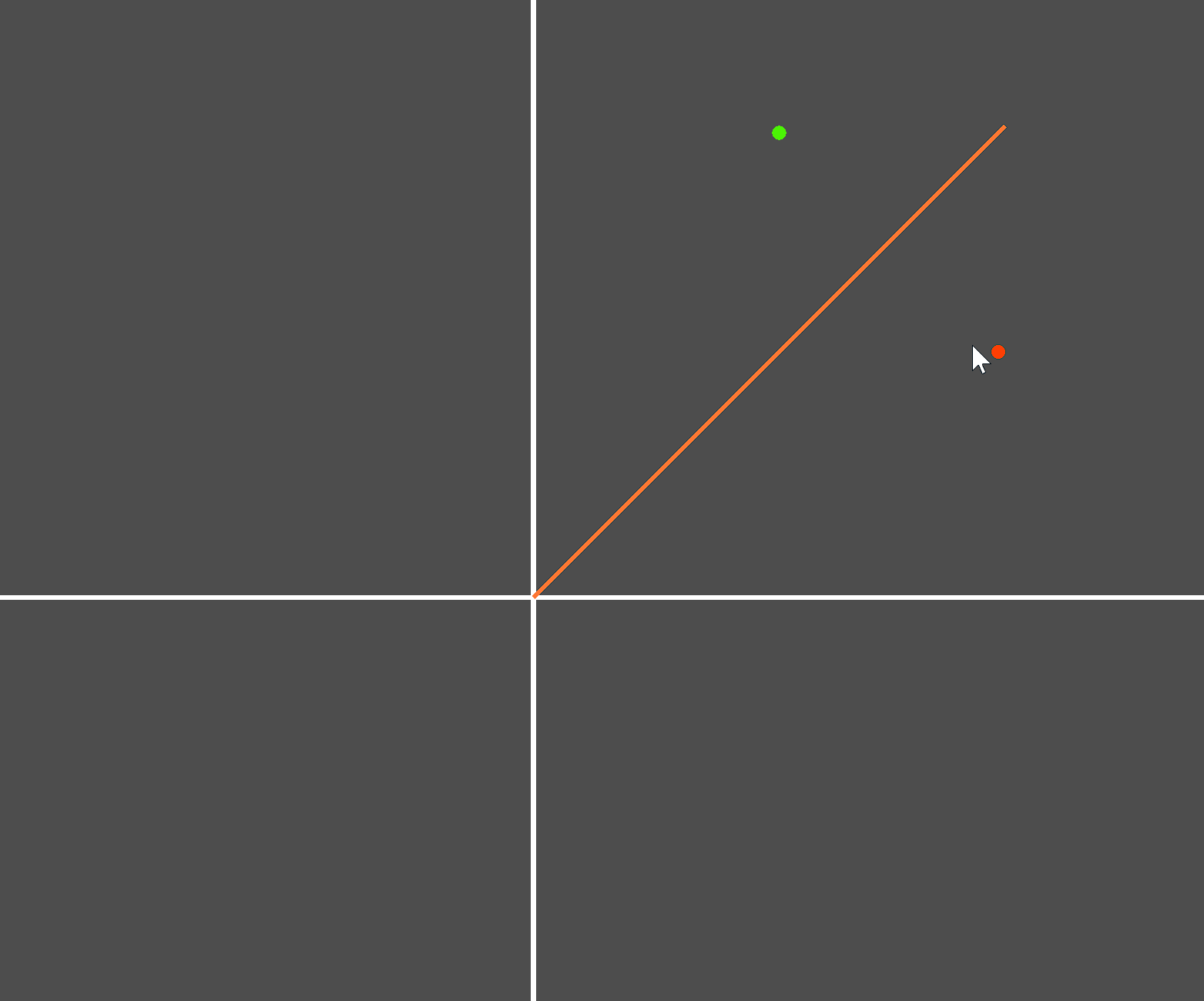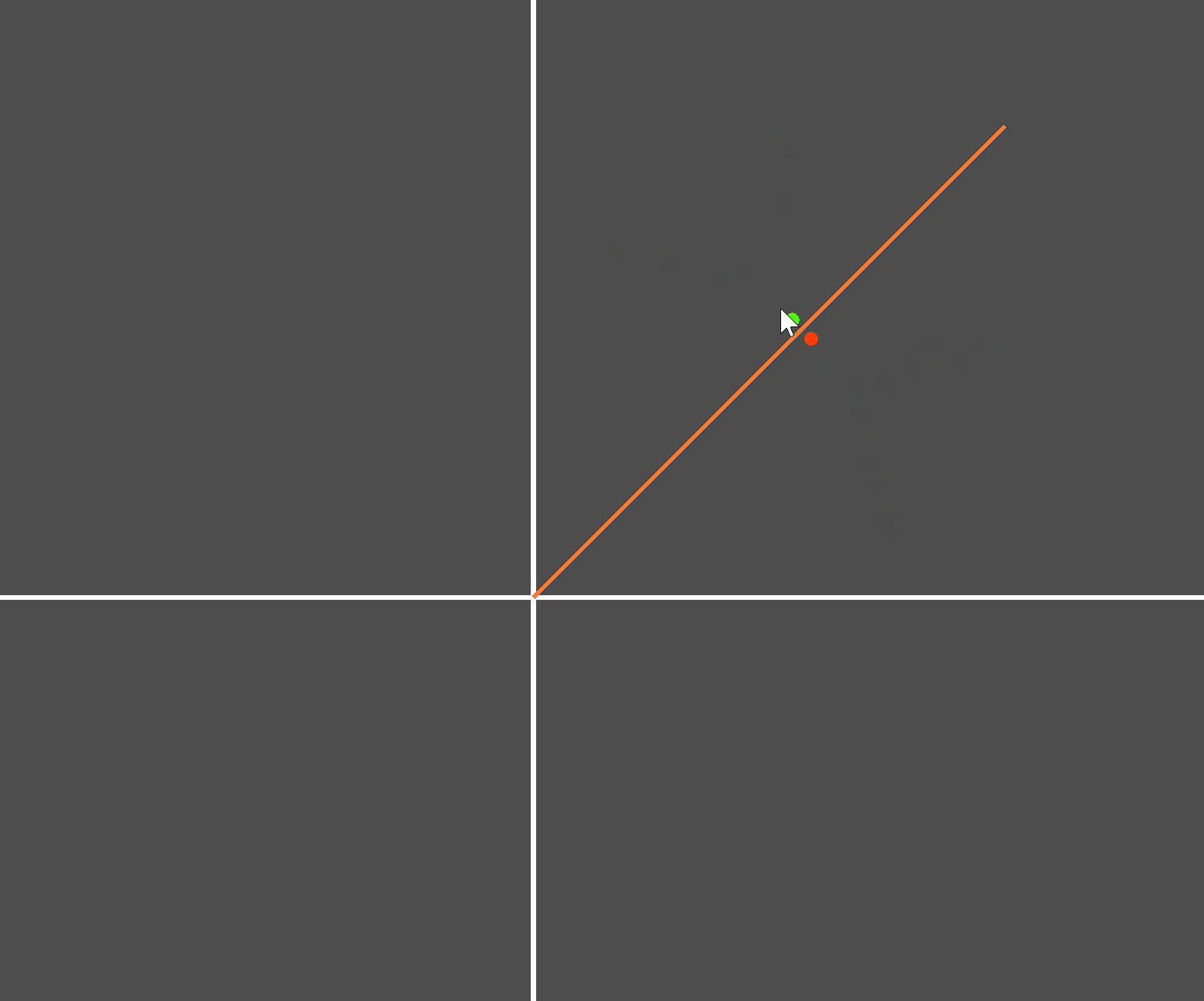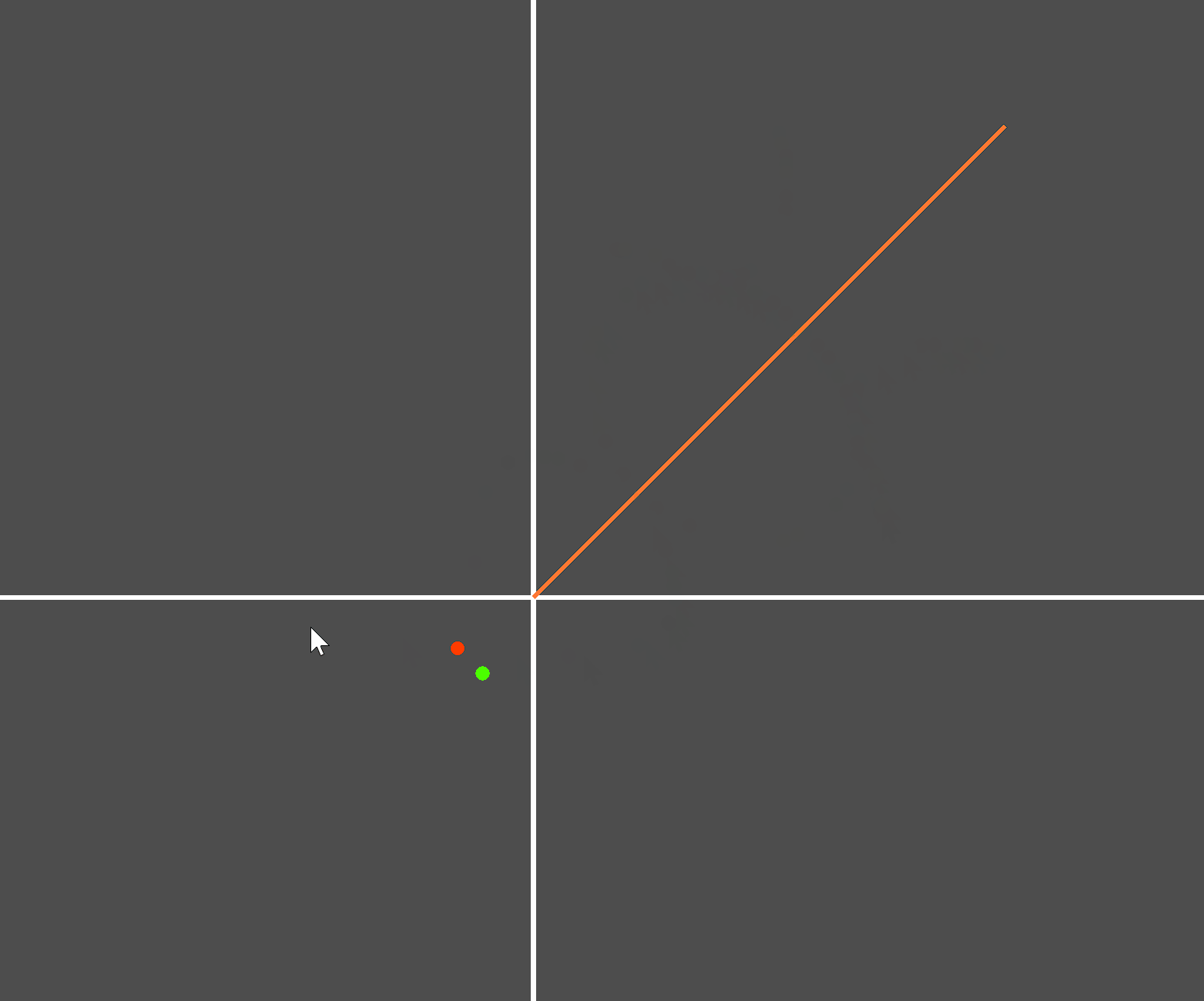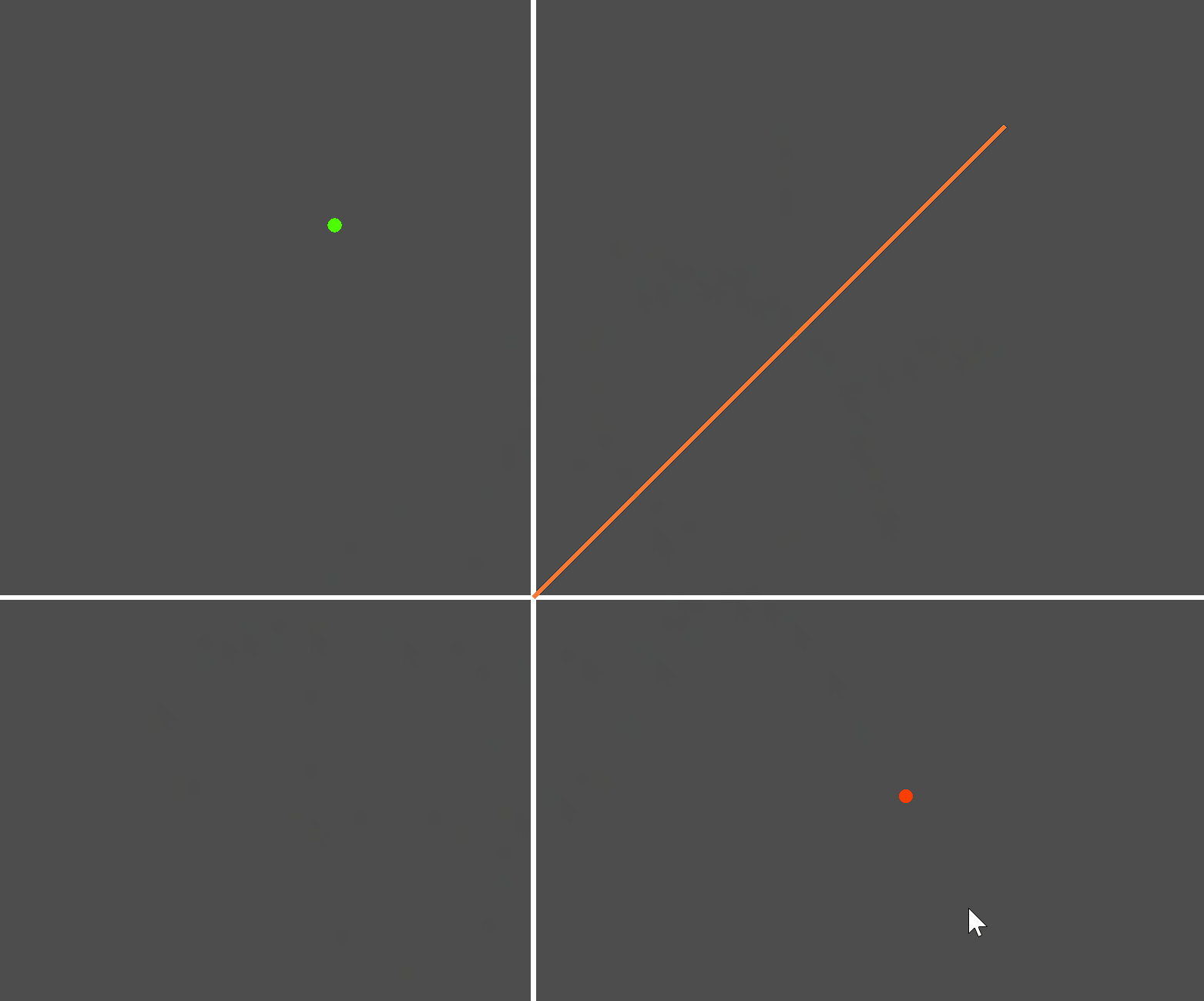
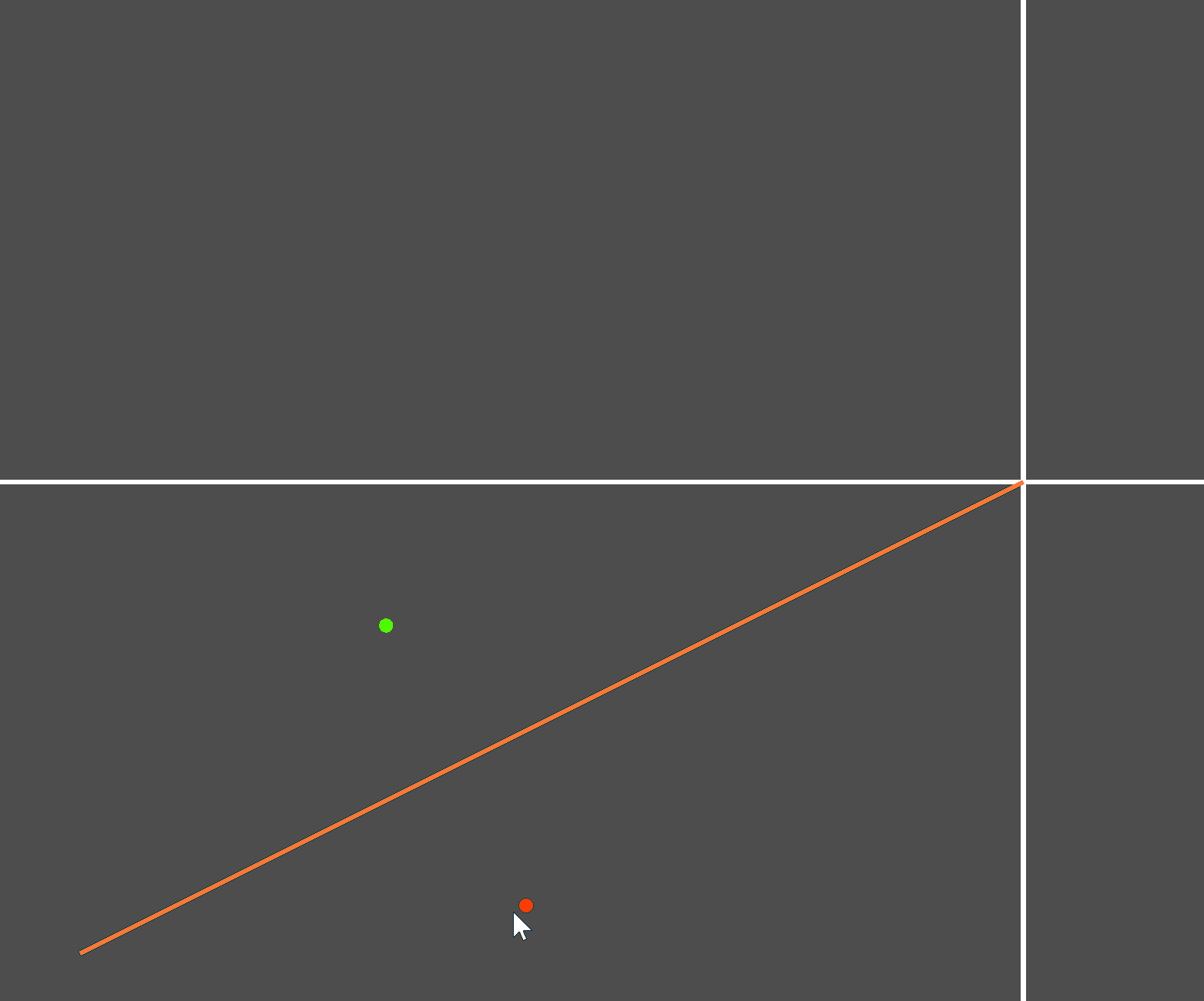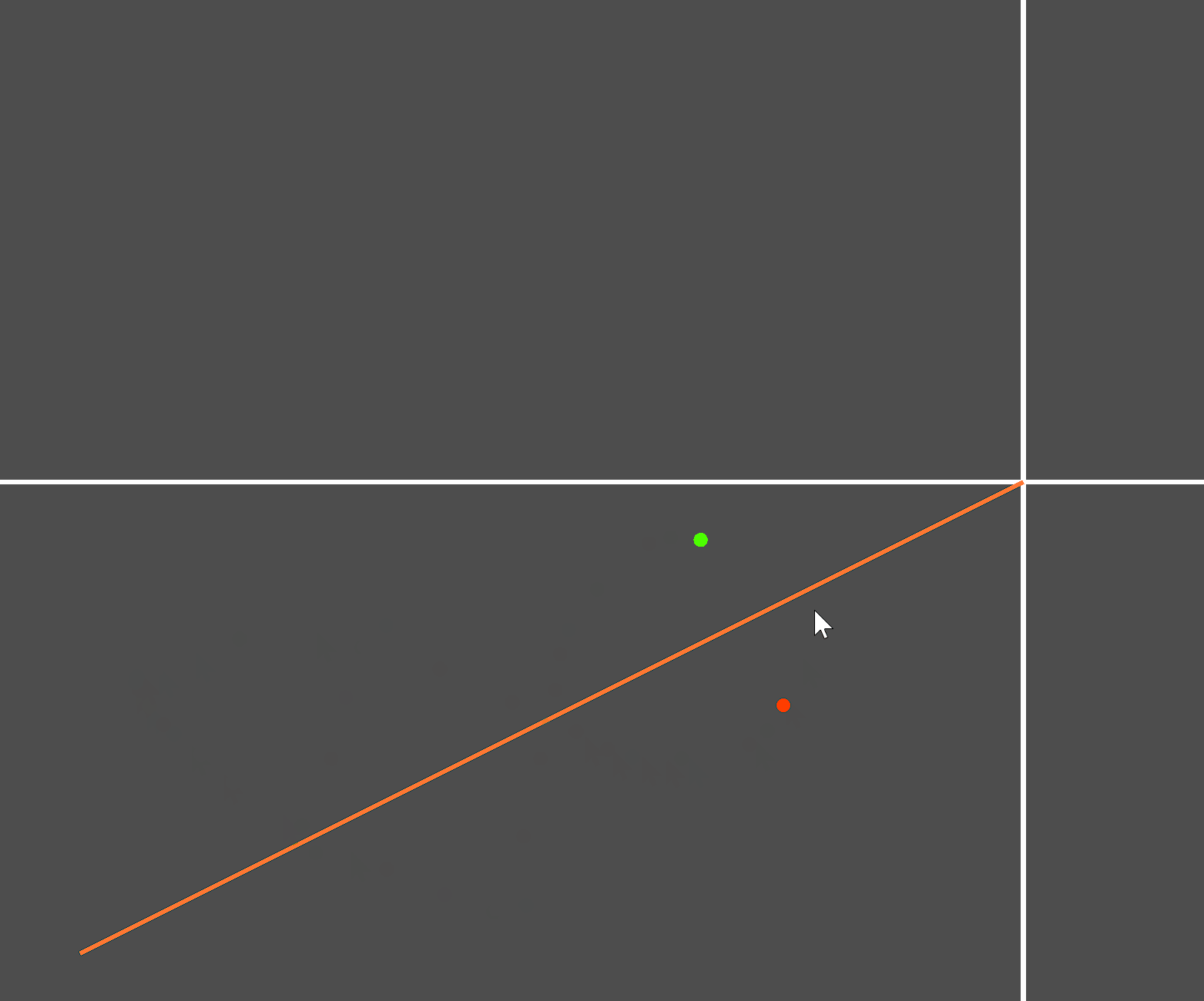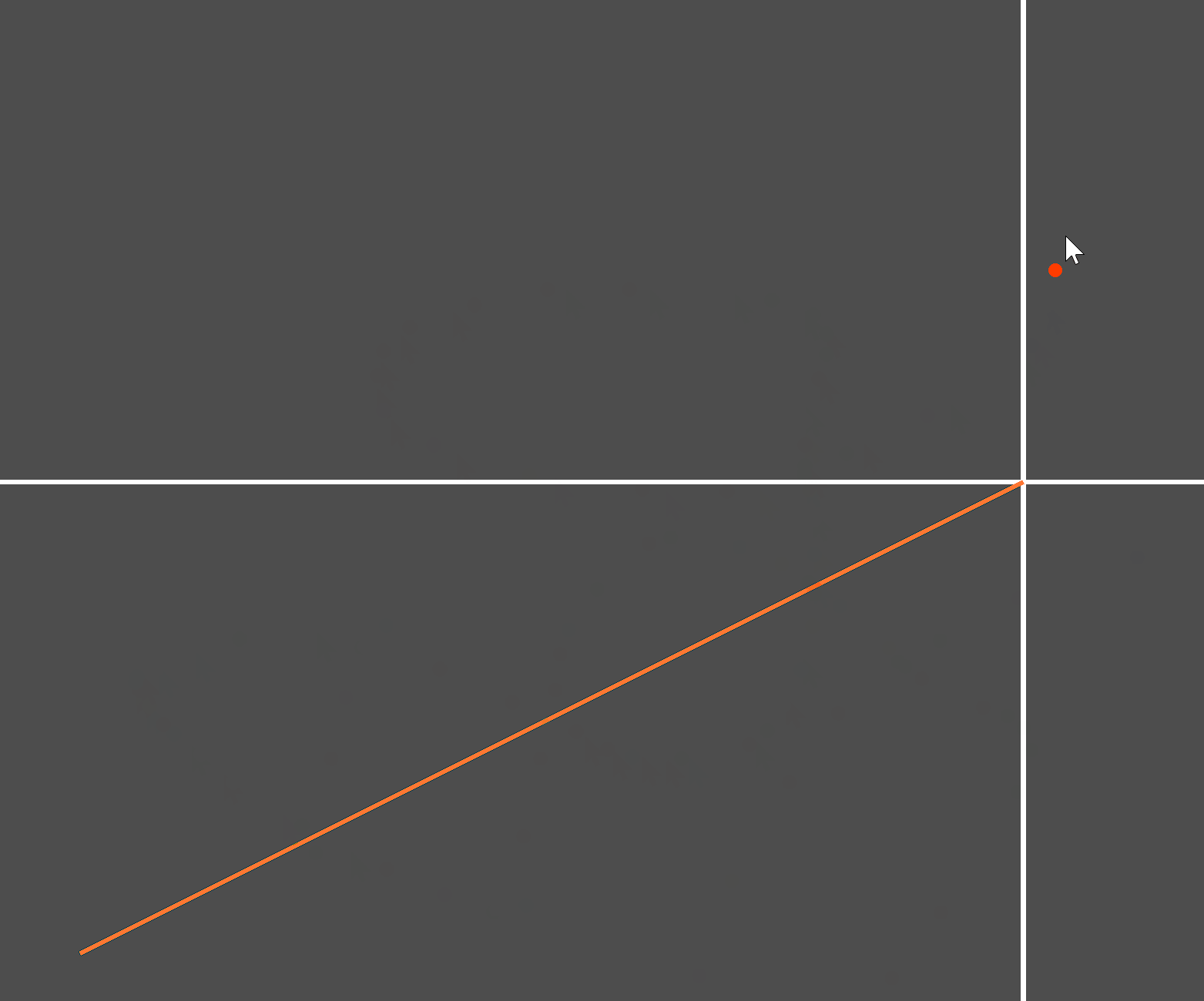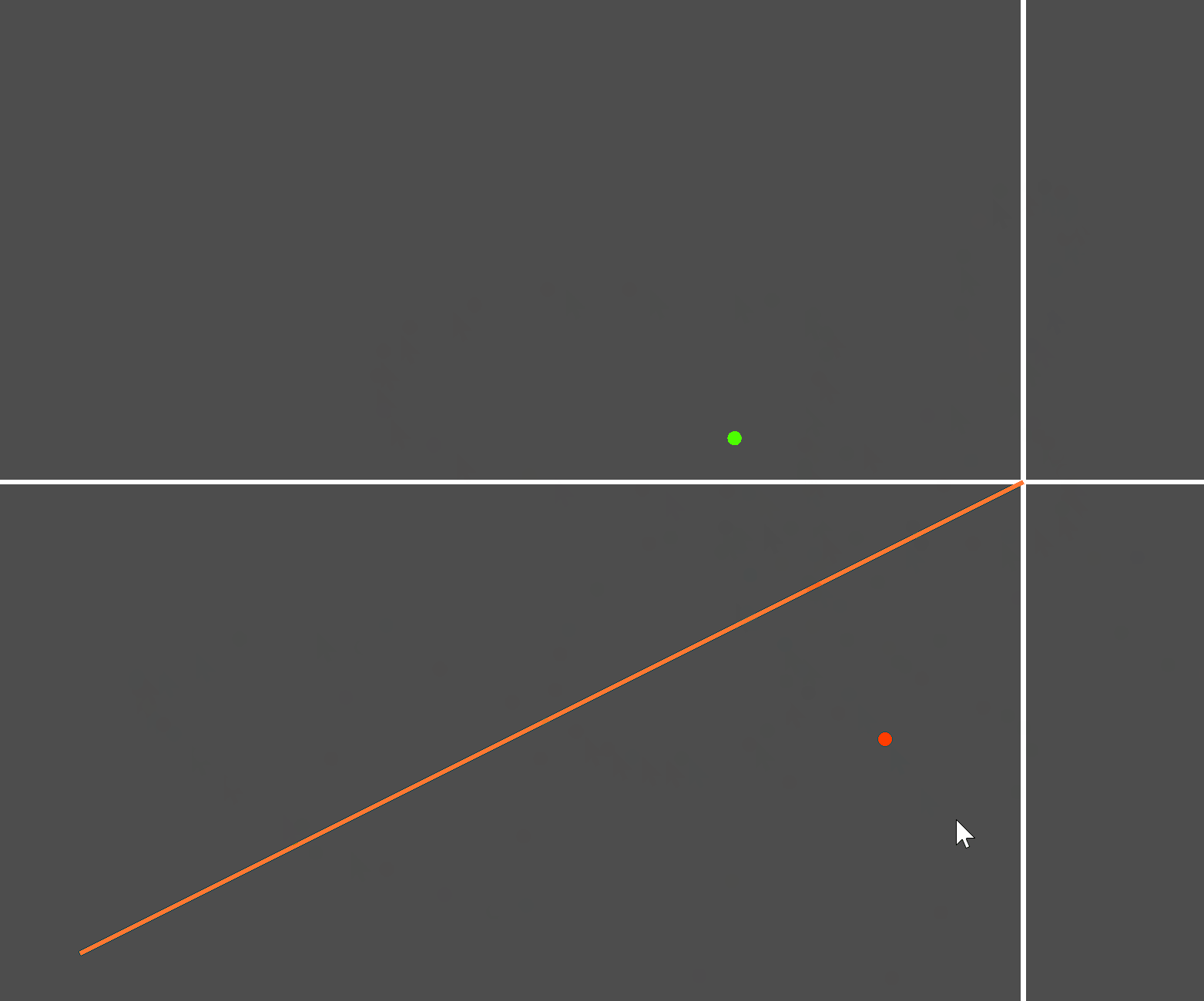
原理和思路有了，接下来测试。创建如下测试场景：

设定窗口拉伸模式：

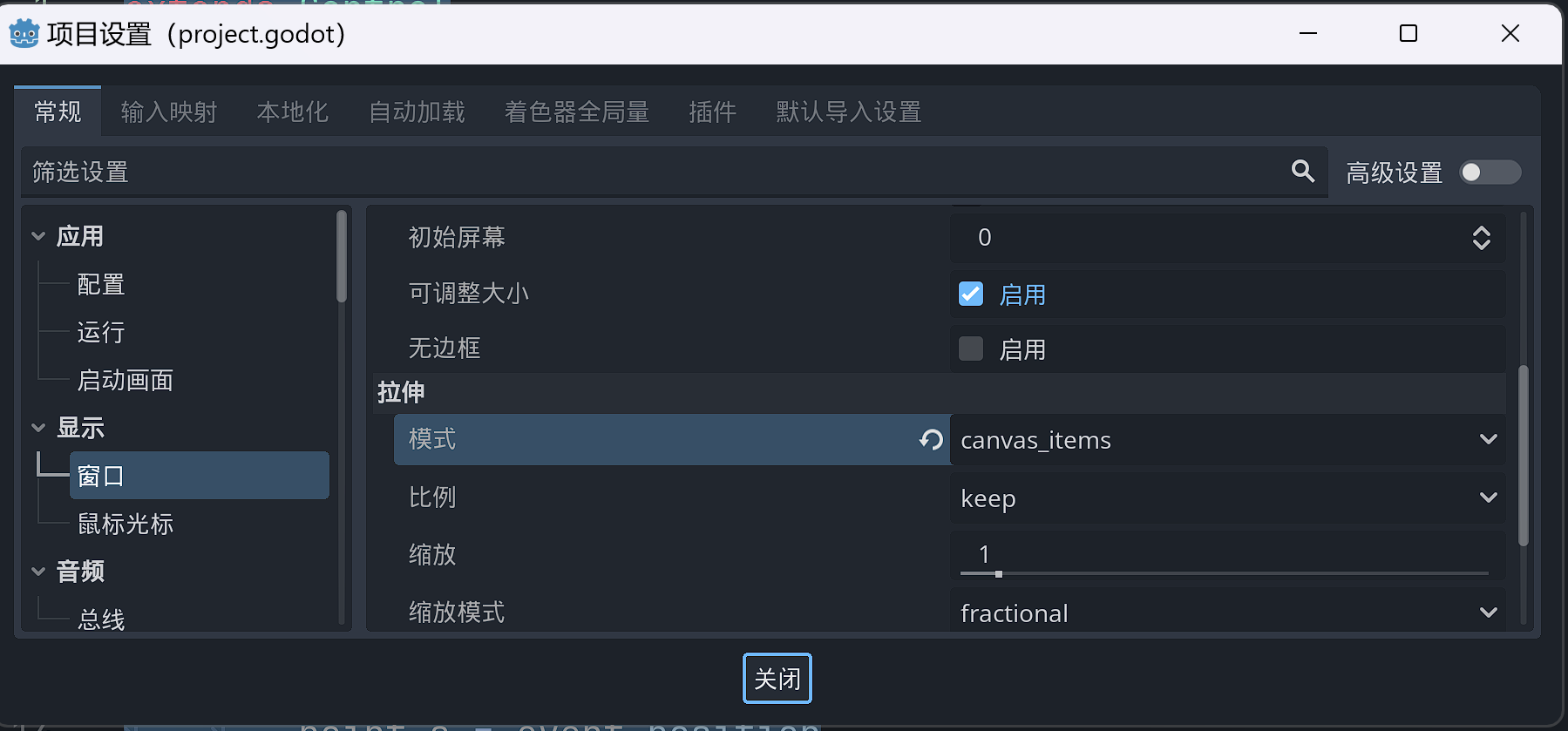
添加如下代码：

extends Control

var dcz = Vector2(-1,1)  # 对称轴
var dcz_length = 200.0  # 对称轴长度
@export var dcz_color:Color = Color.WHITE
@export var point_a_color:Color = Color.WHITE
@export var point_b_color:Color = Color.WHITE

var point_a:Vector2    # 点A


func _input(event):
	if event is InputEventMouseMotion:
		point_a = event.position
		queue_redraw()

func _draw():
	var window_rect:Rect2 = get_rect()             # 控件矩形
	var center:Vector2 = window_rect.get_center()  # 矩形中心
	
	# 在控件中心绘制坐标轴
	draw_line(Vector2(center.x,0),Vector2(center.x,size.y),Color.WHITE,2)
	draw_line(Vector2(0,center.y),Vector2(size.x,center.y),Color.WHITE,2)
	
	# 绘制对称轴
	draw_line(center,center + dcz * dcz_length,dcz_color,2)
	
	# 绘制点A
	draw_circle(point_a,3,point_a_color)
	
	# 求对称点B坐标
	var a = point_a - center  # A点向量的实际值
	var s = a.angle() - dcz.angle()
	var b = a.rotated(- s * 2.0)
	var point_b = b + center
	
	# 绘制对称点B
	draw_circle(point_b,3,point_b_color)

其中：

• dcz为对称轴，用一个向量表示，为了显示的清楚，将其乘以dcz_length。
• 可以分别设定对称轴、A点和B点的颜色：

实际测试：