树上差分

多次对树上的一些路径做加法操作，然后询问某个点或某条边经过操作后的值，就要考虑树上差分了。

点差分

模拟这个过程

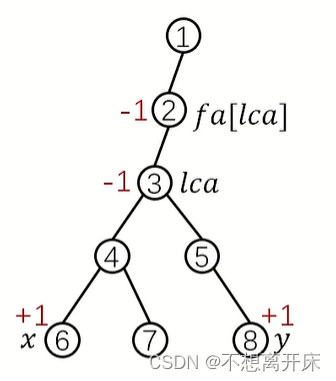
对x到y路径上的点权值均+1，可以等价成对x和y的权值加1，对lca的权值-1，对fa[lca]的权值-1

• 遍历到x，权值为1
• 回溯到4，通过递归求得子树和，得到权值为1，
• 遍历到7，再回溯回4，权值不变
• 回溯到3，权值-1+1为0
• 遍历到5，再遍历到y，y权值为1
• 回溯到5，权值+1为1
• 回溯到3，权值为0+1=1
• 再回溯到2，权值为-1+1=0

故做到了通过一趟dfs就可以求出权值，且不影响其他无关的点

边差分

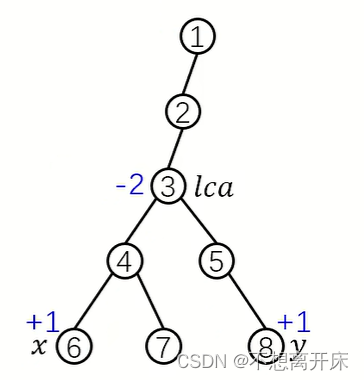
这个模拟的过程和点差分差不多，不过这里边的权值是映射到边下面那个点上，如这个操作是

• x的权值+1，即4到6这条边的权值+1
• y的权值+1，即5到8这条边的权值+1
• lca的权值-2

砍树【蓝桥杯】例题

思路：题目说要砍掉边，其实就是这条边是这些路径的公共边，且走了m次，用边差分，cnt[i]表示编号为i的边走过多少次，即权值，e[i]表示标号为i的点对应的边

#include<iostream>
#include<vector>
using namespace std;
typedef long long LL;
vector<pair<int,int>> v[100005];
LL cnt[100005],f[100005][21],dep[100005],e[100005];
void dfs(int u,int fa)
{
    dep[u]=dep[fa]+1;
    f[u][0]=fa;
    for(int i=1;(1<<i)<=dep[u];i++) f[u][i]=f[f[u][i-1]][i-1];
    for(auto &p:v[u])
    {
        if(p.first==fa) continue;
        dfs(p.first,u);
        //给点赋值对应的边
        e[p.first]=p.second;
    }
}
//求LCA
int lca(int u,int v)
{
    if(dep[u]<dep[v]) swap(u,v);
    for(int i=20;i>=0;i--)
    {
        if(dep[f[u][i]]>=dep[v]) u=f[u][i];
        if(u==v) return u;
    }
    for(int i=20;i>=0;i--)
    {
        if(f[u][i]!=f[v][i]) 
        {
            u=f[u][i];
            v=f[v][i];
        }
    }
    return f[u][0];
}
void dfs2(int u)
{
    for(auto &p:v[u])
    {
        if(p.first==f[u][0]) continue;
        dfs2(p.first);
        cnt[e[u]]+=cnt[e[p.first]];
    }
}
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<n;i++)
    {
        int a,b;
        cin>>a>>b;
        //记录边及编号
        v[a].push_back({b,i});
        v[b].push_back({a,i});
    }
    dfs(1,0);
    for(int i=0;i<m;i++)
    {
        int a,b;
        cin>>a>>b;
        //树上差分边差分操作
        cnt[e[a]]++;
        cnt[e[b]]++;
        cnt[e[lca(a,b)]]-=2;
    }
    //遍历回溯
    dfs2(1);
    int ans=0;
    for(int i=1;i<n;i++)
    {
        if(cnt[i]==m) ans=i;
    }
    cout<<ans<<endl;
    return 0;
}