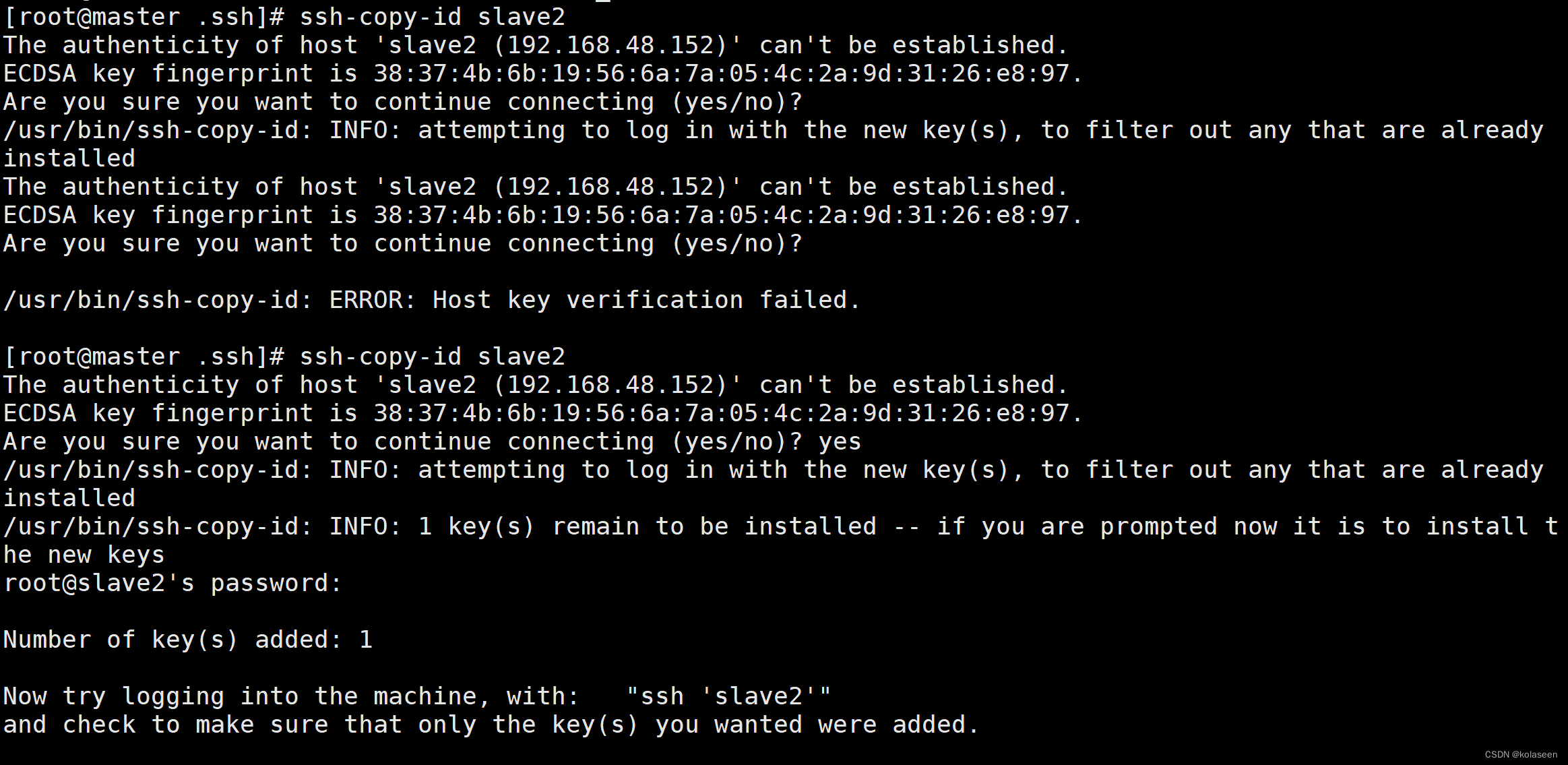
1 梯度下降概念
1.1 概念
梯度下降是一种优化算法,用于最小化一个函数的值,特别是用于训练机器学习模型中的参数,其基本思想是通过不断迭代调整参数的值,使得函数值沿着梯度的反方向逐渐减小,直至达到局部或全局最小值
1.2 理解
在实际业务中,一般多个特征对应一个目标结果值。即对一个多维复杂的方程组的每一维的特征权重进行计算,以求出这个方程局部或全局最小值。如果使用正规方程的进计算,计算量太大,时间及财力消耗巨大。采用梯度下降方法,选定一个经验初始值,一步步沿着梯度的反方向进行计算,使方程解尽快达到收敛,并得出最优解。
1.3 分类
- 批量梯度下降(Batch Gradient Descent)
- 随机梯度下降(Stochastic Gradient Descent)
- 小批量梯度下降(Mini-batch Gradient Descent)
1.4 应用
梯度下降法是机器学习和优化领域中最常用的优化算法之一,被广泛应用于训练神经网络、线性回归、逻辑回归等各种机器学习模型中
2 梯度下降公式
2.1 表达公式
θ n + 1 = θ n − α ∗ g r a d i a n t \theta^{n+1} = \theta^n - \alpha * gradiant θn+1=θn−α∗gradiant
其中
α
\alpha
α表示学习率,
g
r
a
d
i
e
n
t
gradient
gradient表示梯度
θ n + 1 = θ n − α ∗ ∂ J ( θ ) ∂ θ \theta^{n+1} = \theta^n - \alpha * \frac{\partial J (\theta )}{\partial \theta} θn+1=θn−α∗∂θ∂J(θ)
另一种写法
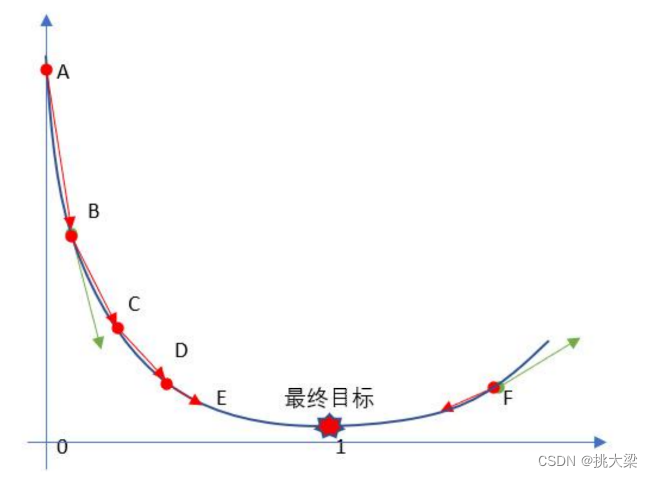
2.2 图示
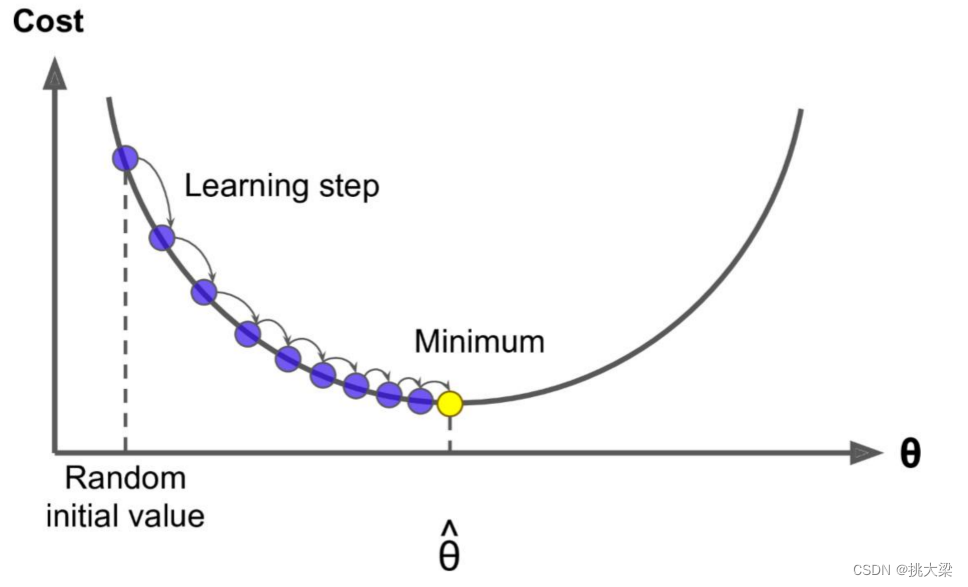
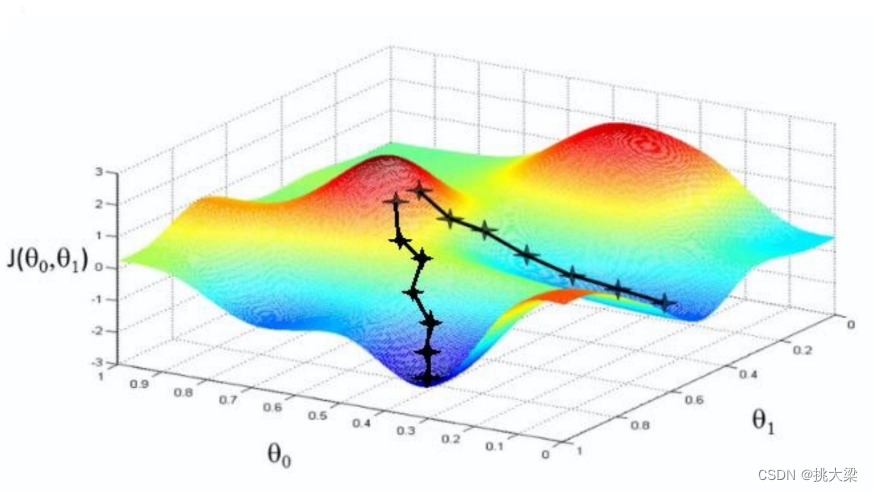
2.3 每一维求解,一起找到 J ( θ ) J(\theta) J(θ)最小值
θ
0
n
+
1
=
θ
0
n
−
α
∗
∂
J
(
θ
)
∂
θ
0
\theta_0^{n+1} = \theta_0^n - \alpha * \frac{\partial J (\theta )}{\partial \theta_0}
θ0n+1=θ0n−α∗∂θ0∂J(θ)
θ
1
n
+
1
=
θ
1
n
−
α
∗
∂
J
(
θ
)
∂
θ
1
\theta_1^{n+1} = \theta_1^n - \alpha * \frac{\partial J (\theta )}{\partial \theta_1}
θ1n+1=θ1n−α∗∂θ1∂J(θ)
θ
m
n
+
1
=
θ
m
n
−
α
∗
∂
J
(
θ
)
∂
θ
m
\theta_m^{n+1} = \theta_m^n - \alpha * \frac{\partial J (\theta )}{\partial \theta_m}
θmn+1=θmn−α∗∂θm∂J(θ)
…
3 梯度下降学习率
3.1 概念
梯度下降算法中的学习率learning rate 是一个非常重要的超参数,它控制了每次参数更新的步长大小。学习率决定了在梯度下降过程中参数更新的速度和稳定性
3.2 理解
为得到局部或全局最小函数值,特征权重按梯度反方向逐渐减小,这个减去的值,就叫作学习率或步长
3.3 调整策略
-
固定学习率: 将学习率设置为一个固定的常数,例如0.01或0.001。这是最简单的学习率调整策略,但可能不够灵活,无法适应不同问题和数据的特性。
-
学习率衰减(Learning Rate Decay): 在训练过程中逐渐减小学习率,以使模型在接近最优解时更加稳定。常见的衰减策略包括指数衰减、分段衰减等。
-
自适应学习率(Adaptive Learning Rate): 根据参数更新的情况动态地调整学习率。例如,AdaGrad、RMSProp、Adam等优化算法会根据梯度的历史信息来自适应地调整学习率,以更有效地更新参数。
-
学习率搜索(Learning Rate Search): 在训练过程中动态地搜索最优的学习率。例如,可以使用学习率范围测试(Learning Rate Range Test)等方法来估计合适的学习率范围。
3.4 应用
-
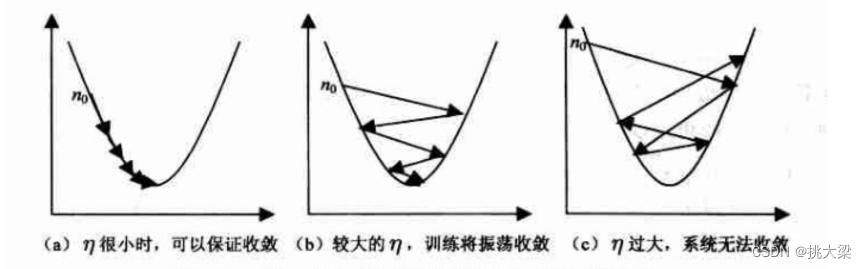
学习率设置得太小,参数更新的步长就会很小,导致收敛速度缓慢,需要更多的迭代次数才能收敛到最优解,或者在达到最优解之前就提前停止。
-
学习率设置得太大,参数更新的步长就会很大,可能导致算法无法收敛,甚至发生震荡或发散。
使用 η \eta η 表示学习率,下图3种学习率情况
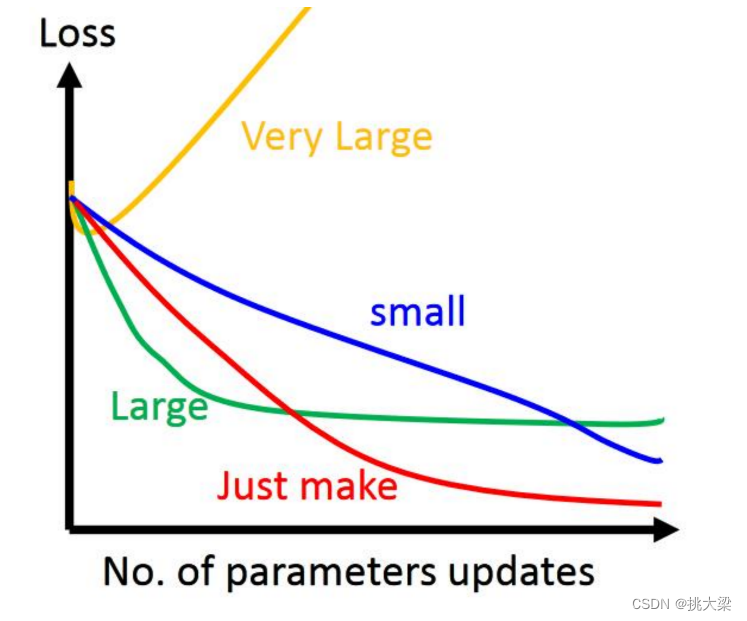
3.5 设置学习率
学习率的是一个经验,把它设置成一个比较小的正整数,0.1、0.01、0.001、0.0001,just make
4 梯度下降实验步骤
- 随机设置最优解 θ \theta θ ,
- 随机生成一组数值 w 0 、 w 1 、 w 2 、 w n w_0、w_1、w_2、w_n w0、w1、w2、wn, 期望 为 0 方差 为 1 的正太分布数据。 、
- 求梯度 g ,梯度代表曲线某点上的切线的斜率,沿着切线往下就相当于沿着坡度最陡峭的方向下降
- if g < 0, 变大,if g > 0, 变小
- 判断是否收敛 convergence,如果收敛跳出迭代,如果没有达到收敛,回第 3 步,继续迭代3~4步
收敛的判断标准是: 随着迭代进行损失函数Loss,变化非常微小甚至不再改变,即认为达到收敛