Machine Learning ---- Multiple linear regression equation

news2024/10/7 16:25:51

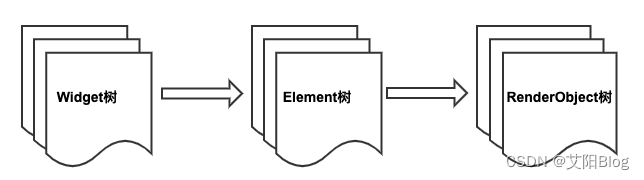
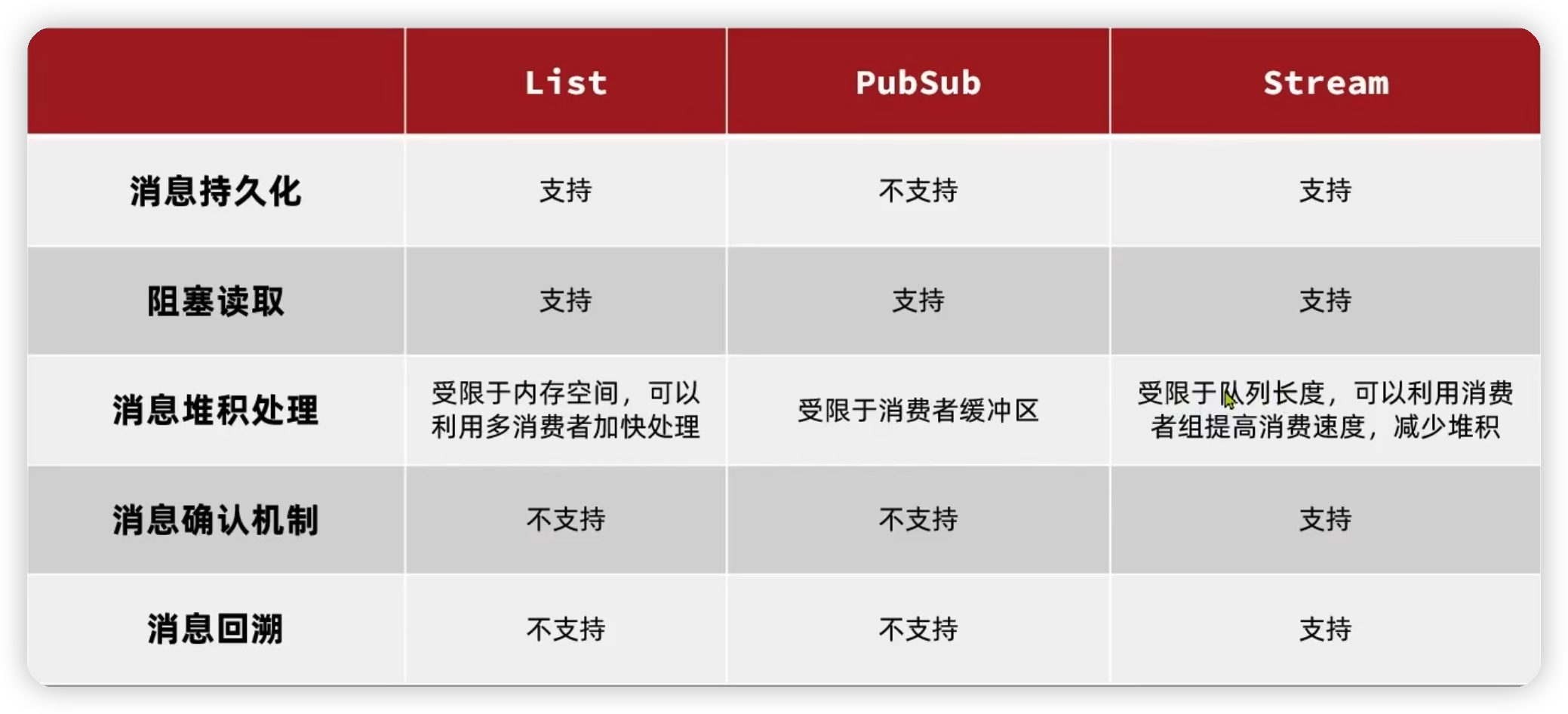
一、Multiple linear regression:

In the study of real-world problems, the changes in the dependent variable are often influenced by several important factors. In this case, it is necessary to use two or more influencing factors as independent variables to explain the changes in the dependent variable. This is known as multiple regression, also known as multiple regression. When there is a linear relationship between multiple independent variables and the dependent variable, the regression analysis conducted is called multiple linear regression.

Let's first review its univariate linear regression equation:

$f(x_i) = wx_i + b$

So, for its multiple linear regression equation, we only need to transform w and x in it:

$f_{\vec{w},b}(\vec{x}) = \vec{w}_i\vec{x}_i + b$

each of $\vec{w}_i$ and $\vec{x}_i$ is a set of vectors，b is a number。

二、Deeply understand：

within this function, $\vec{x}_i = [x_1,x_2.....x_i]$ , $\vec{w}_i = [w_1,w_2.....w_i]$ ,the standard expansion formula is：

$f_{\vec{w},b}(\vec{x}) = \vec{w}_1\vec{x}_1 + \vec{w}_2\vec{x}_2 + \vec{w}_3\vec{x}_3 + ...... + \vec{w}_i\vec{x}_i + b$

That is, the impact of number of $i$ factors on the variable:

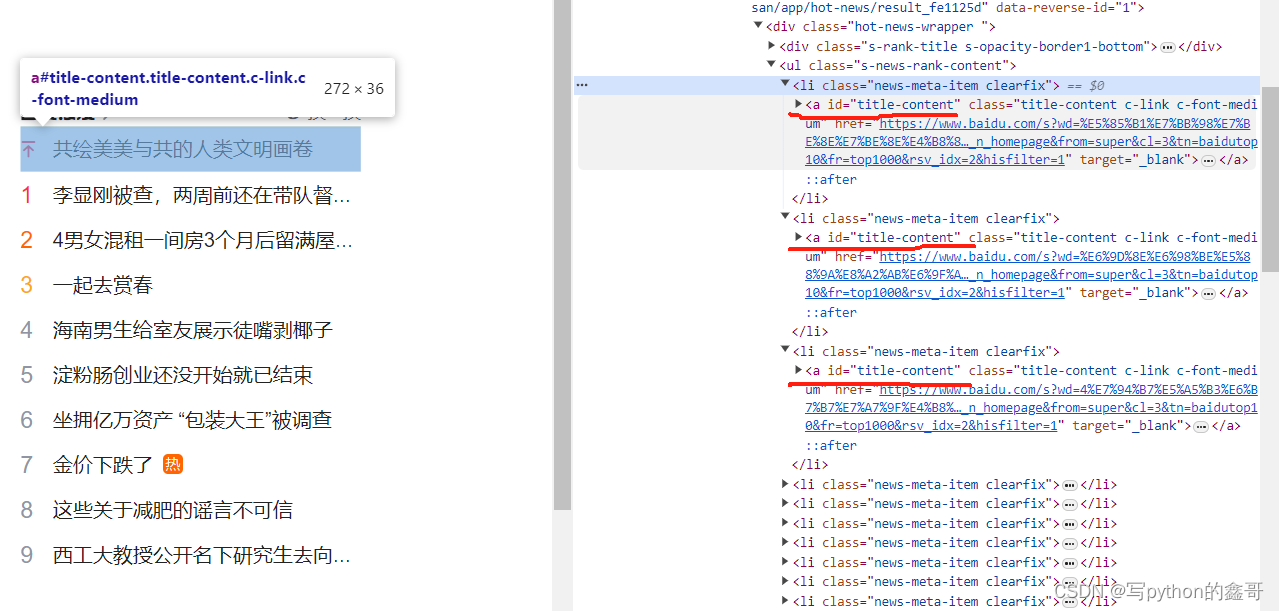
We observe $x_i$ through a table

$x_1$	$x_2$	$x_3$	$f(w,b)$
12	31	33	1222
16	23	67	3215

Each row corresponds to $x$ is a dataset, and each column represents the corresponding influencing factors.

三、Vectorization processing:

For this function:

$f_{\vec{w},b}(\vec{x}) = \vec{w}_1\vec{x}_1 + \vec{w}_2\vec{x}_2 + \vec{w}_3\vec{x}_3 + ...... + \vec{w}_i\vec{x}_i + b$

We transformed it into

$f_{\vec{w},b}(\vec{x}) = \vec{w}_i\vec{x}_i + b$

So in the program, what kind of implementation do we use and what are the differences?

Firstly, when n is not large, we can traverse:

w = np.array([1.0,2.5,-3,3])
b = 4
x = np.array([10,20,30])

f = w[0]*b[0] + w[1]*b[1] + w[2]*b[2] + b

Then, using the for loop method

f = 0
for j in range(0,n):
    f = f + w[j] * x[j]
f = f + b

Finally, we can use the Numpy library:

f = np.dot(w,x) + b

Among the above three methods, it is particularly recommended to use the last one, as the Numpy function can utilize hardware parallel operations. When n is large, the difference in computation speed is particularly significant.