并查集

并查集是大量的树（单个节点也算是树）经过合并生成一系列家族森林的过程。
可以合并可以查询的集合的一种算法
可以查询哪个元素属于哪个集合
每个集合也就是每棵树都是由根节点确定，也可以理解为每个家族的族长就是根节点。
元素集合的代表性元素，也是第一个被分到这个集合的元素
举个数字和字母的例子如下。
初始森林：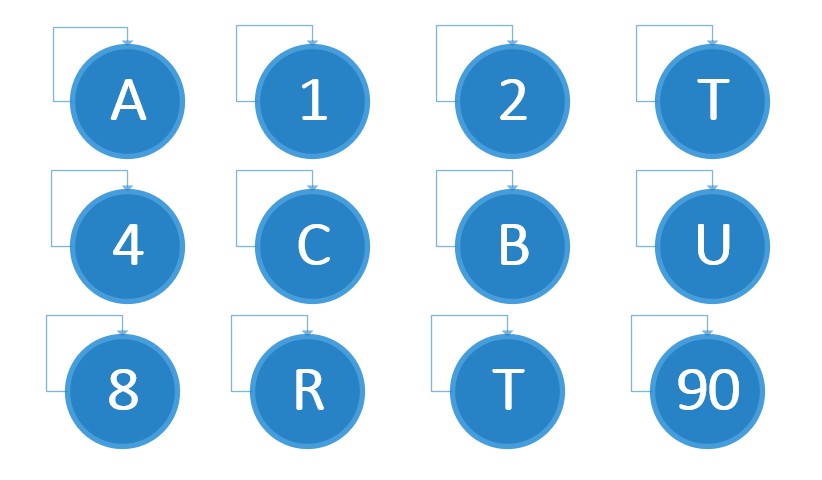
经过的一系列合并后的状态（不唯一，举个栗子）：
A T都是字母集合，把A和T放在同一个集合，A作为T的“介绍人(父亲)“
U T都是字母集合，把U和T放在同一个集合，T作为U的“介绍人(父亲)“
1 2都是数字集合，把1和2放在同一个集合，1作为2的“介绍人(父亲)“
C B都是字母集合，把C和B放在同一个集合，B作为C的“介绍人(父亲)“
2 4都是数字集合，把2和4放在同一个集合，2作为4的“介绍人(父亲)“
C R都是字母集合，把C和R放在同一个集合，C作为R的“介绍人(父亲)“
8 4都是数字集合，把8和4放在同一个集合，4作为8的“介绍人(父亲)“
90 8都是数字集合，把90和8放在同一个集合，8作为90的“介绍人(父亲)“
R I都是字母集合，把R和I放在同一个集合，R作为I的“介绍人(父亲)“

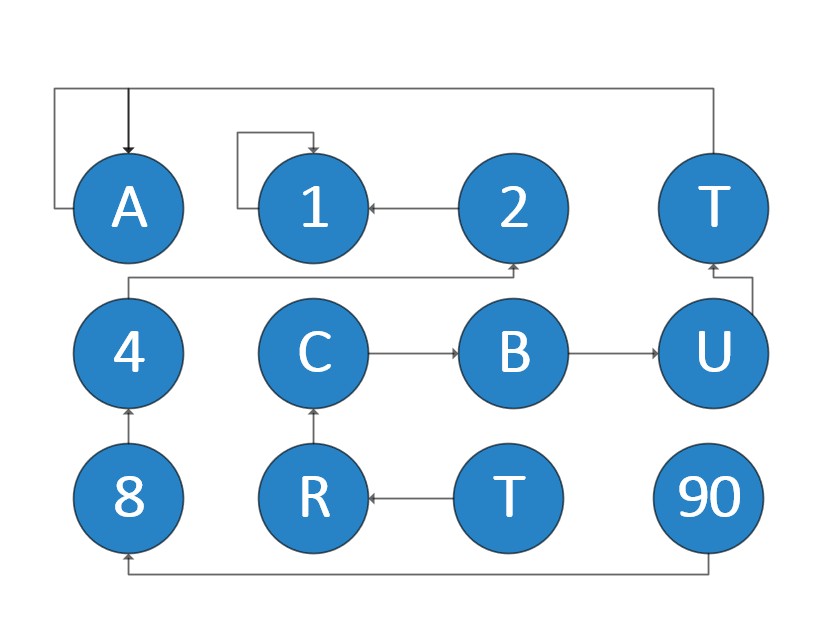
此时A节点的父示是自己，我们杯这种元素为该集合的祖先。用于代表该集合，如A代表的是字母集合。
相似的，1的的父亲是自己，所以1为该集合的祖先，用于代表该数字集合。
我们会发现一个问题，如果查询I属于那个集合，我们要向上跳6次，这非常消耗我们的时间。链式的并查集存储的查询效率太低，在多次查询和大量数据时必定TLE，所以我们需要进行优化，引入路径压缩
最终合并后的状态：
注：示意图的位置与存储物理位置无关，只代表逻辑关系。

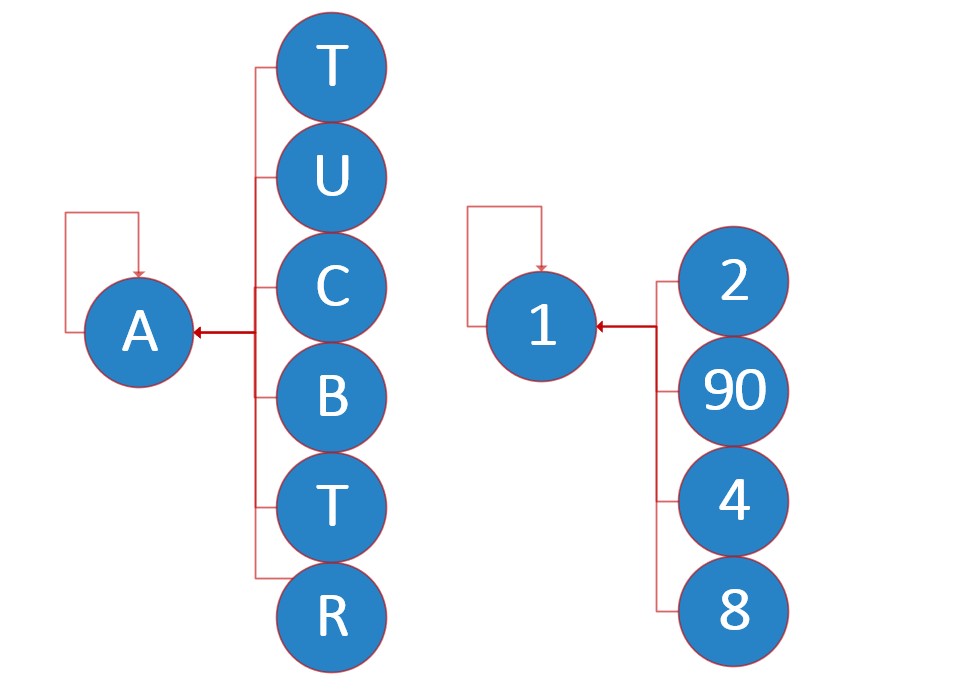
我们每次查询都将路径压缩，使得Fa指针指向祖先节点而不是父节点。在每次合并两个集合时先查询(可选，如果合并过多插入很少可以只在查询时合并)那么最后形成的并查集数据结构会如左图这种形式，此时有着高效的查询效率能够在0(1)的时间复杂度内返回属于什么集合。
这里说的是最后的查询，如果考虑路径压缩的过程时间复杂度应该是$O(\log n)$。

并查集的存储结构

并查集采用数组表示整个森林，初始时每个森林的树根为自己。
C++ 存储与初始化：

# define Maxn 200

// 假设所需数量为200

int fa[Maxn+1]

void init()
{
    for(int i =0;i<=Maxn; i++)
        fa[i]=i;  //i的父亲是i，指向自己
}

查询

一般用递归法实现对代表元素的查询：递归访问父节点，直至根节点（根节点的标志就是父节点是本身）。
根节点相同的两个元素属于同一个集合
所以判断 A，B 是否属于一个集合直接判断 find(A)和 find(B)是否相同即可。
C++ 查询：

int find(int x)
{
    if(fa[x] == x)
        return x;
    else
        return find(fa[x]);
}

我们这里有一个问题，当树的链很长时，比如：

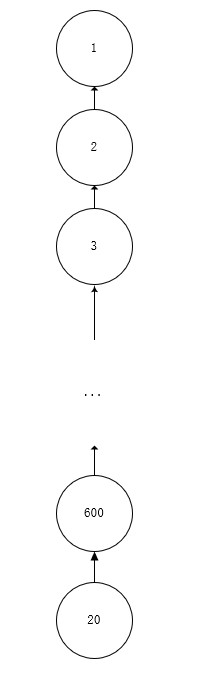
如果每次都查询最后一个，那么他就要经过多次递归，非常消耗时间，这时候我们就要引入路径压缩。

路径压缩

路径压缩是为了解决当树的高度过高的时候，提高查询时效的方法。
解决方式也很简单，在递归的同时将路径压缩，那么上面的图经过一次查询后的效果如下。

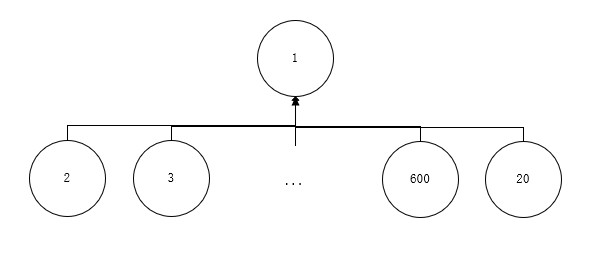
C++ 查询带路径压缩：

int find(int x)
{
    if(x == fa[x])
        return x;

    else
    {
        fa[x] = find(fa[x]);
        //父节点设为根节点

        return fa[x];
        //返回父节点
    }
}

合并

合并的方式很简单，就是把一颗树的根节点设置为另一棵树的根节点即可。
还有一种方式是按秩合并，但是我们使用路径压缩时间复杂度就已经很低了，如果在引入 rank 相对会有些复杂。而且对于我们的使用路径压缩一种方式就已经足够。并且路径压缩和按秩合并一起使用时会影响 rank 准确性，所以我们采用普通的合并与优化后的查找即可。

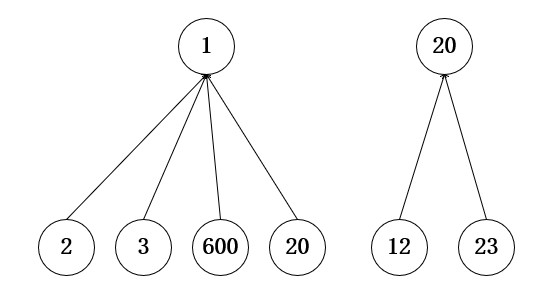
合并后：

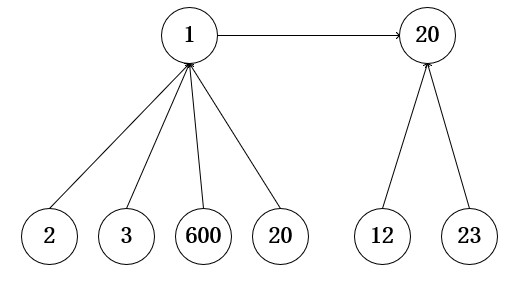
C++ 合并：

void merge(int i, int j)
{
    fa[find(i)] = find(j);
    //把i的祖先挂到j的祖先上面
}

当合并操作远大于查询操作，直接把2的祖先连到12上，这样就只用做一次查询就可以，只用查2的祖先就可以了
不能把2和12简单链接，这样2和2的祖先1之间的线就断了，如果简单地连接过去，就相当于2和12是一个集合，2和原来的不是一个集合了
合并优化：
还有一个优化是启发式合并，有很多的合并算法都叫启发式合并
这里讲其中一种常用的启发式合并。合并时，选择哪棵树的根节点作为新树的根节点会影响未来操作的复杂度。
按照子树大小去合并，小的合并到大的，以免发生退化(以免树的树高变得很高)。
所以启发式合并的原理是在集合合并时将小的集合合并到大的集合里，也可以使 find 操作复杂度降低到 O(logn)，在集合合并时还要增加一个更新集合大小的操作。

C++
void merge(int x,int y)//启发式合并
{
    x=find(x);  //先查x
    y=find(y);  //再查y
    if(x!=y)  //如果x和y不属于同一个集合的话
    {
        if(sz[x]<sz[y])  //判断子树的大小
            swap(x,y);  //如果x小于子树y的话，x是个小树，y是个大树
        sz[x]+=sz[y];   //把y的个数加到x上
        fa[y]=x;      //默认把y树挂到x上，把小树挂到大树上
    }
}

无论子树是高的还是矮的，子树越大
如果把大树的顶点变成了另一棵小的树的分支，实际上这样不好，反而如果把小数的顶点挂到大树的顶点下面，成为分支，这棵挂上去的小树会跟这棵大树下面的其他小树差不多，
如果是一般的并查集题目用路径压缩就可以了，当然两种优化都用的话复杂度可以降得更低。两种优化都使用的话单次操作的复杂度才是 O(α)

按秩合并

除此之外还有一个优化是按秩合并，其实这个合并和启发式合并是有些相似的。合并时，同样会因为选择哪棵树的根节点作为新树的根节点会影响未来操作的复杂度。但这次我们选择是树的秩。秩的意思就是树的高度，按秩合并就是每次合并两个的时候判断两边的树高，小的合并到大的上面去这样。可以将深度较小的树连到另一棵，以免发生退化，也可以使find操作复杂度降低到O(logn)，在集合合并时还要增加一个更新树高的操作。

void merge(int x,int y)//按秩合并
{
	x=find(x);
	y=find(y);
	if(x!=y)
	{
		if(rk[x]>rk[y])  //谁的秩更高一点
			swap(x,y);  //如果x的秩大于y的秩，交换
		f[x]=y;  //将x挂到y上
		if(rk[x]==rk[y])  //如果两个的秩相同
			fk[y]++;  //秩++
	}
}

两种合并的时间复杂度接近都可以认为O(logn)如果使用路径压缩和合并算法时间复杂度同样为 O(a)

合根植物

题目链接
难度: 简单
标签: 并查集, 2017, 国赛
题目描述:
w 星球的一个种植园，被分成 m×n 个小格子（东西方向 m 行，南北方向 n 列）。每个格子里种了一株合根植物。
这种植物有个特点，它的根可能会沿着南北或东西方向伸展，从而与另一个格子的植物合成为一体。
如果我们告诉你哪些小格子间出现了连根现象，你能说出这个园中一共有多少株合根植物吗？
输入描述:
第一行，两个整数 m,n，用空格分开，表示格子的行数、列数（1≤m,n≤1000）。
接下来一行，一个整数 k (0≤k≤10^5 )，表示下面还有 k 行数据。
接下来 k 行，每行两个整数 a，b，表示编号为 a 的小格子和编号为 b 的小格子合根了。
格子的编号一行一行，从上到下，从左到右编号。
比如：5×4 的小格子，编号：

行列	①	②	③	④
①	1	2	3	4
②	5	6	7	8
③	9	10	11	12
④	13	14	15	16
⑤	17	18	19	20

输出描述:

输出植物数量。

输入输出样例:
示例:
输入:

5 4
16
2 3
1 5
5 9
4 8
7 8
9 10
10 11
11 12
10 14
12 16
14 18
17 18
15 19
19 20
9 13
13 17

输出:

5

样例图例如下：

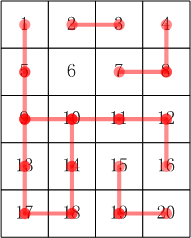
运行限制:

    最大运行时间：1s
    最大运行内存: 256M

题目解析：
这个题就是一个模板并查集的题目，每次合根就是一次 Merge。
最后答案就是看有多少个根即可，那么就是看有多少个fa[x]=x即可。
直接按照题目编写即可，部分解析直接写进题目。
答案解析：
C++ 描述：

#include <bits/stdc++.h>
using namespace std;
# define Maxn 2000000

// 假设所需数量为200
int fa[Maxn+1];  //把0避过去
void init()  //初始化
{
    for(int i =0; i<=Maxn; i++)
        fa[i]=i;
}
int find(int x)  //查询操作，带路径压缩
{
    if(x == fa[x])
        return x;
    else
    {
        fa[x] = find(fa[x]);
        //父节点设为根节点
        return fa[x];
        //返回父节点
    }
}
void merge(int i, int j)  //合根
{
    fa[find(i)] = find(j);
}

int n,m; //n行，m列
int k; //k次合根

int main()
{
    init();
    cin>>n>>m>>k;
    int a,b;
    for(int i=1; i<=k; i++)
    {
        cin>>a>>b;
        merge(a,b); //合根
    }

    int ans=0;
    for(int i=1; i<=n*m; i++)  //从1判断到n*m，判断自己是不是自己的根
    {
        if(fa[i]==i) //找根节点
        {
            ans++;  //如果是自己的根，就代表能找到那棵代表的合根植物
        }
    }
    cout<<ans;  //输出有多少根植物
    return 0;
}