julia语言中的决策树

news2025/1/10 23:31:42

  决策树（Decision Tree）是一种基本的分类与回归方法，它呈现出一种树形结构，可以直观地展示决策的过程和结果。在决策树中，每个内部节点表示一个属性上的判断条件，每个分支代表一个可能的属性值，每个叶节点代表一个类别或者具体的数值。决策树的主要优点是模型具有可读性，分类速度快。

主要算法

构建决策树的主要算法有ID3、C4.5、CART等。这些算法的主要区别在于如何选择最优划分属性。

ID3算法

  以信息增益为准则来选择划分属性。信息增益表示得知特征A的信息而使得类Y的信息不确定性减少的程度。

C4.5算法

  是ID3算法的改进，采用信息增益比来选择划分属性，克服了ID3算法偏向选择取值多的属性的缺点。

CART算法

  既可以用于分类也可以用于回归。CART分类时，使用基尼指数（Gini index）最小化准则来选择划分属性；CART回归时，使用平方误差最小化准则来选择划分属性。

算法公式 

信息熵（Entropy）

  信息熵是度量样本集合纯度最常用的一种指标。它表示随机变量不确定性的度量，也就是数据的混乱程度。信息熵越大，数据的混乱程度越高；信息熵越小，数据的纯度越高。

公式：Ent(S) = -\sum_{k=1}^{n} p_k \log_{2} p_{k}

S是当前样本集合。

p_{k}是集合中第 k类样本所占的比例。

n是类别的总数。

信息熵是通过计算每个类别的概率与其对应的信息量-\log_{2} p_{k}的加权和来得到的。如果所有样本都属于同一类别，则信息熵为0，表示数据完全纯净。

信息增益（Information Gain）

  信息增益表示在得知特征A的信息后，使得类y的信息不确定性减少的程度,它衡量了使用某个特征进行划分后，数据的混乱程度降低了多少,正确的信息增益基于特征 A对数据集 S进行划分后，集合 S的信息熵与划分后各子集信息熵的加权和之差。

公式：Gain(A) = Ent(S) - \sum_{v \in Values(A)} \frac{|S_v|}{|S|} Ent(S_v)

A是待考察的特征。

Values(A)是特征 A所有可能取值的集合。

S_{v}是集合 S 中特征 A 取值为 v 的子集。

|S_{v}| 和 |S|分别表示集合 S_v 和 S 的元素数量。

信息增益比（Information Gain Ratio)

  信息增益比是为了校正信息增益容易偏向于选择取值较多的特征的问题而提出的。它通过引入一个称为分裂信息熵的项来惩罚取值较多的特征。

SplitEntropy(A) = -\sum_{v \in Values(A)} \frac{|S_v|}{|S|} \log_{2} \frac{|S_v|}{|S|}

信息增益比则是信息增益与分裂信息熵的比值：

GainRatio(A) = \frac{Gain(A)}{SplitEntropy(A)}

分裂信息熵衡量了按照特征 A进行划分时产生的信息量的多少。将其与信息增益结合使用，可以平衡特征取值多少对选择的影响。

基尼指数（Gini Index）

  基尼指数是另一种度量数据混乱程度的指标。与信息熵类似，基尼指数越小，数据的纯度越高。

Gini(S) = 1 - \sum_{k=1}^{n} p_k^2

基尼指数通过从1中减去每个类别的概率的平方和来计算。当所有样本都属于同一类别时，基尼指数为0。当类别分布均匀时，基尼指数达到最大值1 - \frac{1}{n}对于 n个类。因此，基尼指数越小，表示集合中被选中的样本被分错的概率越小，即集合的纯度越高。

 构建决策树

决策树的构建通常包括以下几个步骤：

特征选择

  从训练数据的特征集合中选择一个特征作为当前节点的划分标准。按照所选特征的每一个取值，将训练数据集划分为若干子集，使得每个子集在当前特征上具有相同的取值。

决策树生成

  根据所选特征评估标准（如信息增益、信息增益比、基尼指数等），从根节点开始，递归地生成子节点。直到满足停止条件（如达到最大深度、所有样本属于同一类别、划分后的样本数小于预设阈值等）。

决策树剪枝

  为了避免过拟合，可以对决策树进行剪枝。剪枝分为预剪枝（在决策树生成过程中进行）和后剪枝（在决策树生成后进行）。通过剪枝，可以删除一些不必要的分支，使决策树更加简洁和高效。

分类与回归

  使用生成的决策树对新的数据进行分类或回归预测。从根节点开始，根据新数据的特征值，沿着决策树向下遍历，直到到达某个叶节点，该叶节点所代表的类别或数值即为预测结果。

 

使用Julia语言实现

  以下代码于 DecisionTree包  官方示例有进行修改，在使用前需安装DecisionTree包和ScikitLearn包、KnetMetrics包：

# 加载 DecisionTree 软件包
using DecisionTree

分离 Fisher 的 Iris 数据集要素和标注

features, labels = load_data("iris")    # 同样可以查看 "adult" 和 "digits" 数据集  
  
# 加载的数据类型是 Array{Any}  
# 为了获得更好的性能，将它们转换为具体的类型  
features = float.(features)  
labels   = string.(labels)
修剪树分类器
# 训练一个深度受限的分类器  
model = DecisionTreeClassifier(max_depth=2)  
fit!(model, features, labels)  
# 以美观的格式打印决策树，深度为 5 个节点（可选）  
print_tree(model, 5)  
# 应用已训练的模型  
predict(model, [5.9,3.0,5.1,1.9])  
# 获取每个标签的概率  
predict_proba(model, [5.9,3.0,5.1,1.9])  
println(get_classes(model)) # 返回 predict_proba 输出中的列顺序  
# 在 3 折交叉验证上运行  
# 请查看 ScikitLearn.jl 了解安装说明  
using ScikitLearn.CrossValidation: cross_val_score  
accuracy = cross_val_score(model, features, labels, cv=3)

 输出决策树

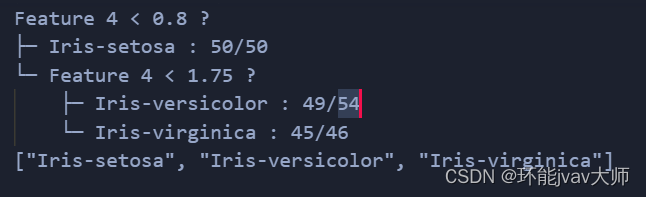
原生API

决策树分类器
using KnetMetrics
using DecisionTree

features, labels = load_data("iris")    # 同样可以查看 "adult" 和 "digits" 数据集  
  
# 加载的数据类型是 Array{Any}  
# 为了获得更好的性能，将它们转换为具体的类型  
features = float.(features)  
labels   = string.(labels)

# 训练完整的决策树分类器  
model = build_tree(labels, features)  
  
# 修剪决策树：合并纯度大于等于90%的叶子节点（默认值为100%）  
# 这里的纯度指的是节点中样本属于同一类别的比例  
model = prune_tree(model, 0.9)  
  
# 以美观的格式打印决策树，深度为5个节点（可选）  
# 这有助于我们可视化决策树的结构和决策过程  
print_tree(model, 5)  
  
# 应用已训练的模型进行预测  
apply_tree(model, [5.9,3.0,5.1,1.9])  
  
# 将模型应用于所有样本，得到预测结果  
preds = apply_tree(model, features)  
  
# 生成混淆矩阵，以及准确率和Kappa分数  
# 混淆矩阵可以帮助我们了解模型的分类性能  
confusion_matrix(labels, preds)  
  
# 获取每个标签的概率  
# 这对于需要了解分类置信度的场景很有用  
apply_tree_proba(model, [5.9,3.0,5.1,1.9], ["Iris-setosa", "Iris-versicolor", "Iris-virginica"])  
  
# 对修剪后的决策树进行3折交叉验证  
# 交叉验证是一种评估模型性能的方法，可以帮助我们了解模型在未知数据上的表现  
n_folds = 3  
accuracy = nfoldCV_tree(labels, features, n_folds)  
  
# 设置分类参数及其默认值  
# 这些参数可以控制决策树的构建和修剪过程，从而影响模型的性能  
# pruning_purity: 用于后修剪的纯度阈值（默认值：1.0，不进行修剪）  
# max_depth: 决策树的最大深度（默认值：-1，没有最大深度限制）  
# min_samples_leaf: 每个叶子节点所需的最小样本数（默认值：1）  
# min_samples_split: 进行分裂所需的最小样本数（默认值：2）  
# min_purity_increase: 分裂所需的最小纯度增加量（默认值：0.0）  
# n_subfeatures: 随机选择的特征数（默认值：0，保留所有特征）  
# rng: 使用的随机数生成器或种子（默认值：Random.GLOBAL_RNG）  
n_subfeatures = 0; max_depth = -1; min_samples_leaf = 1; min_samples_split = 2  
min_purity_increase = 0.0; pruning_purity = 1.0; seed = 3  
  
# 使用指定的参数构建决策树分类器  
model = build_tree(labels, features,  
                   n_subfeatures,  
                   max_depth,  
                   min_samples_leaf,  
                   min_samples_split,  
                   min_purity_increase;  
                   rng = seed)  
  
# 使用指定的参数进行n折交叉验证，并返回准确率  
# verbose参数设置为true可以打印出详细的验证过程信息  
accuracy = nfoldCV_tree(labels, features,  
                        n_folds,  
                        pruning_purity,  
                        max_depth,  
                        min_samples_leaf,  
                        min_samples_split,  
                        min_purity_increase;  
                        verbose = true,  
                        rng = seed)

输出模型

Feature 3 < 2.45 ?
├─ Iris-setosa : 50/50
└─ Feature 4 < 1.75 ?
    ├─ Feature 3 < 4.95 ?
        ├─ Iris-versicolor : 47/48
        └─ Feature 4 < 1.55 ?
            ├─ Iris-virginica : 3/3
            └─ Feature 1 < 6.95 ?
                ├─ Iris-versicolor : 2/2
                └─ Iris-virginica : 1/1
    └─ Feature 3 < 4.85 ?
        ├─ Feature 1 < 5.95 ?
            ├─ Iris-versicolor : 1/1
            └─ Iris-virginica : 2/2
        └─ Iris-virginica : 43/43
Fold 1
Classes:  ["Iris-setosa", "Iris-versicolor", "Iris-virginica"]
Matrix:   3×3 Matrix{Int64}:
 16   0   0
  0  14   0
  0   1  19
Accuracy: 0.98
Kappa:    0.9697702539298669

Fold 2
Classes:  ["Iris-setosa", "Iris-versicolor", "Iris-virginica"]
Matrix:   3×3 Matrix{Int64}:
 18   0   0
  0  12   3
  0   3  14
Accuracy: 0.88
Kappa:    0.819494584837545

Fold 3
Classes:  ["Iris-setosa", "Iris-versicolor", "Iris-virginica"]
Matrix:   3×3 Matrix{Int64}:
 16   0   0
  0  19   2
  0   0  13
Accuracy: 0.96
Kappa:    0.9393939393939393

Mean Accuracy: 0.94

Fold 1
Classes:  ["Iris-setosa", "Iris-versicolor", "Iris-virginica"]
Matrix:   3×3 Matrix{Int64}:
 19   0   0
  0  15   2
  0   2  12
Accuracy: 0.92
Kappa:    0.8790810157194682

Fold 2
Classes:  ["Iris-setosa", "Iris-versicolor", "Iris-virginica"]
Matrix:   3×3 Matrix{Int64}:
 16   0   0
  0  14   2
  0   1  17
Accuracy: 0.94
Kappa:    0.9097472924187725

Fold 3
Classes:  ["Iris-setosa", "Iris-versicolor", "Iris-virginica"]
Matrix:   3×3 Matrix{Int64}:
 15   0   0
  0  17   0
  0   0  18
Accuracy: 1.0
Kappa:    1.0

Mean Accuracy: 0.9533333333333333
 随机森林分类器 
# 训练随机森林分类器  
# 使用2个随机特征，10棵树，每棵树使用0.5的样本比例，最大树深度为6  
model = build_forest(labels, features, 2, 10, 0.5, 6)  
  
# 应用已学习的模型  
apply_forest(model, [5.9,3.0,5.1,1.9])  
  
# 获取每个标签的概率  
apply_forest_proba(model, [5.9,3.0,5.1,1.9], ["Iris-setosa", "Iris-versicolor", "Iris-virginica"])  
  
# 对森林进行3折交叉验证，每次分割使用2个随机特征  
n_folds=3; n_subfeatures=2  
accuracy = nfoldCV_forest(labels, features, n_folds, n_subfeatures)  
  
# 分类参数及其默认值设置  
# n_subfeatures: 每次分割要考虑的随机特征数（默认值：-1，即特征数的平方根）  
# n_trees: 要训练的树的数量（默认值：10）  
# partial_sampling: 每棵树训练所需的样本比例（默认值：0.7）  
# max_depth: 决策树的最大深度（默认值：无最大限制）  
# min_samples_leaf: 每个叶子节点所需的最小样本数（默认值：5）  
# min_samples_split: 分割所需的最小样本数（默认值：2）  
# min_purity_increase: 分割所需的最小纯度增加量（默认值：0.0）  
# 关键字 rng: 使用的随机数生成器或种子（默认值：Random.GLOBAL_RNG）  
#              多线程森林必须使用Int类型的种子  
n_subfeatures=-1; n_trees=10; partial_sampling=0.7; max_depth=-1  
min_samples_leaf=5; min_samples_split=2; min_purity_increase=0.0; seed=3  
  
model = build_forest(labels, features,  
                     n_subfeatures,  
                     n_trees,  
                     partial_sampling,  
                     max_depth,  
                     min_samples_leaf,  
                     min_samples_split,  
                     min_purity_increase;  
                     rng = seed)  
  
accuracy = nfoldCV_forest(labels, features,  
                          n_folds,  
                          n_subfeatures,  
                          n_trees,  
                          partial_sampling,  
                          max_depth,  
                          min_samples_leaf,  
                          min_samples_split,  
                          min_purity_increase;  
                          verbose = true,  
                          rng = seed)

输出结果

Fold 1
Classes:  ["Iris-setosa", "Iris-versicolor", "Iris-virginica"]
Matrix:   3×3 Matrix{Int64}:
 15   0   0
  0  18   1
  0   1  15
Accuracy: 0.96
Kappa:    0.9396863691194209

Fold 2
Classes:  ["Iris-setosa", "Iris-versicolor", "Iris-virginica"]
Matrix:   3×3 Matrix{Int64}:
 15   0   0
  0  12   2
  0   2  19
Accuracy: 0.92
Kappa:    0.877899877899878

Fold 3
Classes:  ["Iris-setosa", "Iris-versicolor", "Iris-virginica"]
Matrix:   3×3 Matrix{Int64}:
 20   0   0
  0  14   3
  0   1  12
Accuracy: 0.92
Kappa:    0.878787878787879

Mean Accuracy: 0.9333333333333332

Fold 1
Classes:  ["Iris-setosa", "Iris-versicolor", "Iris-virginica"]
Matrix:   3×3 Matrix{Int64}:
 19   0   0
  0  15   2
  0   2  12
Accuracy: 0.92
Kappa:    0.8790810157194682

Fold 2
Classes:  ["Iris-setosa", "Iris-versicolor", "Iris-virginica"]
Matrix:   3×3 Matrix{Int64}:
 16   0   0
  0  13   3
  0   1  17
Accuracy: 0.92
Kappa:    0.8795180722891568

Fold 3
Classes:  ["Iris-setosa", "Iris-versicolor", "Iris-virginica"]
Matrix:   3×3 Matrix{Int64}:
 15   0   0
  0  17   0
  0   3  15
Accuracy: 0.94
Kappa:    0.9099099099099098

Mean Accuracy: 0.9266666666666667
 自适应增强决策树桩分类器
# train adaptive-boosted stumps, using 7 iterations
model, coeffs = build_adaboost_stumps(labels, features, 7);
# apply learned model
apply_adaboost_stumps(model, coeffs, [5.9,3.0,5.1,1.9])
# get the probability of each label
apply_adaboost_stumps_proba(model, coeffs, [5.9,3.0,5.1,1.9], ["Iris-setosa", "Iris-versicolor", "Iris-virginica"])
# 对boosted stumps进行3折交叉验证，使用7次迭代
n_iterations=7; n_folds=3
accuracy = nfoldCV_stumps(labels, features,
                          n_folds,
                          n_iterations;
                          verbose = true)

输出结果

old 1
Classes:  ["Iris-setosa", "Iris-versicolor", "Iris-virginica"]
Matrix:   3×3 Matrix{Int64}:
 18   0   0
  0  15   0
  0   4  13
Accuracy: 0.92
Kappa:    0.880239520958084

Fold 2
Classes:  ["Iris-setosa", "Iris-versicolor", "Iris-virginica"]
Matrix:   3×3 Matrix{Int64}:
 17   0   0
  0  17   2
  0   0  14
Accuracy: 0.96
Kappa:    0.9399038461538461

Fold 3
Classes:  ["Iris-setosa", "Iris-versicolor", "Iris-virginica"]
Matrix:   3×3 Matrix{Int64}:
 15   0   0
  0  15   1
  0   4  15
Accuracy: 0.9
Kappa:    0.8500299940011996

Mean Accuracy: 0.9266666666666666

 

回归示例 
n, m = 10^3, 5
features = randn(n, m)
weights = rand(-2:2, m)
labels = features * weights

 回归树 

using DecisionTree

features, labels = load_data("iris")    # also see "adult" and "digits" datasets

n, m = 10^3, 5
features = randn(n, m)
weights = rand(-2:2, m)
labels = features * weights

# 训练回归树  
model = build_tree(labels, features)  
# 应用已学习的模型  
apply_tree(model, [-0.9,3.0,5.1,1.9,0.0])  
# 运行3折交叉验证，返回决定系数（R^2）的数组  
n_folds = 3  
r2 = nfoldCV_tree(labels, features, n_folds)  
  
# 回归参数集及其相应的默认值  
# pruning_purity: 用于后剪枝的纯度阈值（默认：1.0，不剪枝）  
# max_depth: 决策树的最大深度（默认：-1，无最大值）  
# min_samples_leaf: 每个叶子所需的最小样本数（默认：5）  
# min_samples_split: 分裂所需的最小样本数（默认：2）  
# min_purity_increase: 分裂所需的最小纯度（默认：0.0）  
# n_subfeatures: 随机选择的特征数（默认：0，保留所有）  
# 关键字 rng: 要使用的随机数生成器或种子（默认 Random.GLOBAL_RNG）  
n_subfeatures = 0; max_depth = -1; min_samples_leaf = 5  
min_samples_split = 2; min_purity_increase = 0.0; pruning_purity = 1.0 ; seed=3  
  
model = build_tree(labels, features,  
                   n_subfeatures,  
                   max_depth,  
                   min_samples_leaf,  
                   min_samples_split,  
                   min_purity_increase;  
                   rng = seed)  
  
r2 =  nfoldCV_tree(labels, features,  
                   n_folds,  
                   pruning_purity,  
                   max_depth,  
                   min_samples_leaf,  
                   min_samples_split,  
                   min_purity_increase;  
                   verbose = true,  
                   rng = seed)

输出结果

Fold 1
Mean Squared Error:     1.1192402911257475
Correlation Coeff:      0.9472838062763782
Coeff of Determination: 0.8971356247350447

Fold 2
Mean Squared Error:     1.111874839232273
Correlation Coeff:      0.9348375925443003
Coeff of Determination: 0.8736744843129887

Fold 3
Mean Squared Error:     1.183298319862818
Correlation Coeff:      0.9341422313248625
Coeff of Determination: 0.8705440012888646

Mean Coeff of Determination: 0.8804513701122992

Fold 1
Mean Squared Error:     1.0323579387631954
Correlation Coeff:      0.9422656678561453
Coeff of Determination: 0.8862358467110852

Fold 2
Mean Squared Error:     1.0151297530543415
Correlation Coeff:      0.9447969369155476
Coeff of Determination: 0.8926327449004646

Fold 3
Mean Squared Error:     1.085847261851617
Correlation Coeff:      0.9460144474841884
Coeff of Determination: 0.894208955983675

Mean Coeff of Determination: 0.8910258491984083
 回归随机森林 
# 训练回归森林，使用2个随机特征，10棵树，
# 每个叶子平均5个样本，每棵树使用0.7的样本比例
model = build_forest(labels, features, 2, 10, 0.7, 5)
# apply learned model
apply_forest(model, [-0.9,3.0,5.1,1.9,0.0])
# run 3-fold cross validation on regression forest, using 2 random features per split
n_subfeatures=2; n_folds=3
r2 = nfoldCV_forest(labels, features, n_folds, n_subfeatures)

#=
build_forest()函数的回归参数集及其相应的默认值
n_subfeatures: 每次分割要考虑的随机特征数（默认：-1，即特征数的平方根）
n_trees: 要训练的树的数量（默认：10）
partial_sampling: 每棵树训练所需的样本比例（默认：0.7）
max_depth: 决策树的最大深度（默认：无最大值）
min_samples_leaf: 每个叶子所需的最小样本数（默认：5）
min_samples_split: 分裂所需的最小样本数（默认：2）
min_purity_increase: 分裂所需的最小纯度（默认：0.0）
关键字 rng: 要使用的随机数生成器或种子（默认：Random.GLOBAL_RNG）
多线程森林必须使用Int类型的种子
=#

n_subfeatures=-1; n_trees=10; partial_sampling=0.7; max_depth=-1
min_samples_leaf=5; min_samples_split=2; min_purity_increase=0.0; seed=3

model = build_forest(labels, features,
                     n_subfeatures,
                     n_trees,
                     partial_sampling,
                     max_depth,
                     min_samples_leaf,
                     min_samples_split,
                     min_purity_increase;
                     rng = seed)

r2 =  nfoldCV_forest(labels, features,
                     n_folds,
                     n_subfeatures,
                     n_trees,
                     partial_sampling,
                     max_depth,
                     min_samples_leaf,
                     min_samples_split,
                     min_purity_increase;
                     verbose = true,
                     rng = seed)

输出结果

Fold 1
Mean Squared Error:     1.3599903131498468
Correlation Coeff:      0.9515587356817066
Coeff of Determination: 0.8663047566031118

Fold 2
Mean Squared Error:     1.3831299735363378
Correlation Coeff:      0.9477732726231708
Coeff of Determination: 0.8548766665136407

Fold 3
Mean Squared Error:     1.3108585932358423
Correlation Coeff:      0.9444344709074005
Coeff of Determination: 0.856713400894658

Mean Coeff of Determination: 0.8592982746704702

Fold 1
Mean Squared Error:     1.3542680364781128
Correlation Coeff:      0.9470579766572528
Coeff of Determination: 0.8566121773382684

Fold 2
Mean Squared Error:     1.3027839706551103
Correlation Coeff:      0.9472514130926669
Coeff of Determination: 0.8685137573058215

Fold 3
Mean Squared Error:     1.0809211711553741
Correlation Coeff:      0.9587274410123069
Coeff of Determination: 0.8851291475337838

Mean Coeff of Determination: 0.8700850273926246
 保存模型

模型可以保存到磁盘，并使用 JLD2.jl 包重新加载。 

using JLD2
@save "model_file.jld2" model

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1524595.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

JavaSE、JavaEE和Jakarta EE的历史、区别与联系

JavaSE、JavaEE和Jakarta EE的历史、区别与联系

JavaSE、JavaEE和Jakarta EE是Java平台中的三个重要组成部分&#xff0c;它们各自承担着不同的角色&#xff0c;同时也有着密切的联系。在理解它们之间的历史、区别和联系之前&#xff0c;我们首先需要了解它们的基本概念。 JavaSE&#xff08;Java Standard Edition&#xff…
阅读更多...
电脑充电器能充手机吗？如何给手机充电？

电脑充电器能充手机吗？如何给手机充电？

电脑充电器可以给手机充电吗&#xff1f; 电脑充电器可以给手机充电&#xff0c;但前提是电脑充电器的功率输出与手机的功率匹配且接口匹配。 假设电脑充电器的输出功率为5V/2A&#xff0c;手机也支持5V/2A的输入功率。 只要接口匹配&#xff0c;就可以使用电脑充电器给手机充…
阅读更多...
基于单片机的光电传感转速测量系统的设计

基于单片机的光电传感转速测量系统的设计

摘要：针对在工程实践中很多场合都需要对转速这一参数进行精准测量的目的，采用以STC89C52 芯片为核心，结合转动系统、光电传感器、显示模块等构成光电传感器转速测量系统，实现对电机 转速的测量。通过测试表明该系统具有结构简单、所耗成本低，测量精度高、稳定可靠等优点，…
阅读更多...
Day67：WEB攻防-Java安全JNDIRMILDAP五大不安全组件RCE执行不出网

Day67：WEB攻防-Java安全JNDIRMILDAP五大不安全组件RCE执行不出网

知识点&#xff1a; 1、Java安全-RCE执行-5大类函数调用 2、Java安全-JNDI注入-RMI&LDAP&高版本 3、Java安全-不安全组件-Shiro&FastJson&JackJson&XStream&Log4j Java安全-RCE执行-5大类函数调用 Java中代码执行的类&#xff1a; GroovyRuntimeExecPr…
阅读更多...
html5cssjs代码 023 公制计量单位进位与换算表

html5cssjs代码 023 公制计量单位进位与换算表

html5&css&js代码 023 公制计量单位进位与换算表 一、代码二、解释 这段HTML代码定义了一个网页&#xff0c;用于展示公制计量单位的进位与换算表。 一、代码 <!DOCTYPE html> <html lang"zh-cn"> <head><meta charset"utf-8&quo…
阅读更多...
将FastSAM中的TextPrompt迁移到MobileSAM中

将FastSAM中的TextPrompt迁移到MobileSAM中

本博文简单介绍了SAM、FastSAM与MobileSAM，主要关注于TextPrompt功能的使用。从性能上看MobileSAM是最实用的，但其没有提供TextPrompt功能，故而参考FastSAM中的实现，在MobileSAM中嵌入TextPrompt类。并将TextPrompt能力嵌入到MobileSAM官方项目提供的gradio.py部署代码中，…
阅读更多...
ros小问题之差速轮式机器人轮子不显示（rviz gazebo）

ros小问题之差速轮式机器人轮子不显示（rviz gazebo）

在rviz及gazebo练习差速轮式机器人时&#xff0c;很奇怪&#xff0c;只有个机器人的底板及底部的两个万向轮&#xff0c;如下图&#xff0c; 后来查看相关.xacro文件&#xff0c;里面是引用包含了轮子的xacro文件&#xff0c;只需传入不同的参数即可调用生成不同位置的轮子&…
阅读更多...
ARM_基础之RAS

ARM_基础之RAS

Reliability, Availability, and Serviceability (RAS), for A-profile architecture 源自 https://developer.arm.com/documentation/102105/latest/ 1 Introduction to RAS 1.1 Faults,Errors,and failures 三个概念的区分&#xff1a; • A failure is the event of devia…
阅读更多...
IDEA系列软件设置自动换行

IDEA系列软件设置自动换行

以pycharm软件为例&#xff0c;我们在编程的时候常常会遇到这种情况&#xff0c;内容过长导致超出pycharm的界面&#xff0c;导致我们阅读浏览起来非常的不方便&#xff0c;对于这种情况&#xff0c;我们可以通过给IDEA软件设置自动换行来解决 首先打开setting&#xff0c;找到…
阅读更多...
MySQL_数据库图形化界面软件_00000_00001

MySQL_数据库图形化界面软件_00000_00001

目录 NavicatSQLyogDBeaverMySQL Workbench可能出现的问题 Navicat 官网地址&#xff1a; 英文&#xff1a;https://www.navicat.com 中文&#xff1a;https://www.navicat.com.cn SQLyog 官网地址&#xff1a; 英文&#xff1a;https://webyog.com DBeaver 官网地址&…
阅读更多...
odoo17开发教程（6）：用户界面UI的交互-创建Action

odoo17开发教程（6）：用户界面UI的交互-创建Action

前面的文章中我们已经创建了新模型及其相应的访问权限&#xff0c;是时候与用户界面进行交互了。 数据文件&#xff08;XML&#xff09; 在上一篇文章中&#xff0c;我们通过 CSV 文件添加数据。当要加载的数据格式简单时&#xff0c;CSV 格式很方便。当格式比较复杂时&#x…
阅读更多...
Javaweb学习记录（一）Maven

Javaweb学习记录（一）Maven

Maven是一款Java项目管理工具&#xff0c;下面将介绍Maven的实际作用和相关的操作 Maven项目依赖的添加 在Maven项目中添加依赖&#xff0c;通过dependencies标签添加所有依赖&#xff0c;所有依赖都添加在里面&#xff0c;而单个依赖就使用dependency标签添加进项目&#xf…
阅读更多...
【数据结构入门】顺序表详解（增删查改）

【数据结构入门】顺序表详解（增删查改）

目录 顺序表的基本概念 动态顺序表的实现 初始化 插入 尾插法 头插法 指定位置之前插入 删除 尾删法 头删法 指定位置删除 查找 销毁 顺序表的基本概念 什么是顺序表&#xff1f; 顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构&#xff0c;一般…
阅读更多...
elasticsearch基础学习

elasticsearch基础学习

elasticsearch简介 什么是elasticsearch elasticsearch&#xff08;简称es&#xff09;&#xff0c;其核心是 Elastic Stack&#xff0c;es是一个基于 Apache Lucene&#xff08;TM&#xff09;的开源的高扩展的分布式全文检索引擎&#xff0c;它可以近乎实时的存储、检索数据…
阅读更多...
软考 系统架构设计师之回归及知识点回顾（7）

软考 系统架构设计师之回归及知识点回顾（7）

接前一篇文章&#xff1a;软考 系统架构设计师之回归及知识点回顾&#xff08;6&#xff09; 11. 云计算 背景 大数据和云计算已成为IT领域的两种主流技术。“数据是重要资产”这一概念已成为大家的共识&#xff0c;众多公司争相分析、挖掘大数据背后的重要财富。同时学术界、…
阅读更多...
深度学习pytorch——Broadcast自动扩展

深度学习pytorch——Broadcast自动扩展

介绍 在 PyTorch 中&#xff0c;Broadcast 是指自动扩展&#xff08;broadcasting&#xff09;运算的功能。它允许用户在不同形状的张量之间执行运算&#xff0c;而无需手动将它们的形状改变为相同的大小。当进行运算时&#xff0c;PyTorch 会自动调整张量的形状&#xff0c;使…
阅读更多...
数据结构的基本框架以及泛型

数据结构的基本框架以及泛型

目录 集合框架复杂度大O的渐进表示法 装包(箱)或者拆包(箱)装包拆包 泛型泛型的上界泛型方法求最大值 集合框架 Java的集合框架,Java Collection Framework 又被称为容器container, 定义在java.util包下的一组 interfaces 和其实现类 classes interface: 接口 abstracb class…
阅读更多...
RuoYi-Vue开源项目3-登录操作代码解析

RuoYi-Vue开源项目3-登录操作代码解析

登录操作代码解析 前端代码详解 // 1. 登录按钮点击触发登录事件 handleLogin<el-button:loading"loading"size"medium"type"primary"style"width:100%;"click.native.prevent"handleLogin"><span v-if"!load…
阅读更多...
ElasticSearch：数据的魔法世界

ElasticSearch：数据的魔法世界

​ 欢迎来到ElasticSearch的奇妙之旅&#xff01;在这个充满魔法的搜索引擎世界中&#xff0c;数据不再是沉闷的数字和字母&#xff0c;而是变得充满活力和灵动。无论你是刚刚踏入数据探索的小白&#xff0c;还是已经对搜索引擎有所了解的行者&#xff0c;本篇博客都将为你揭示…
阅读更多...
【从零开始学习数据结构 | 第一篇】树

【从零开始学习数据结构 | 第一篇】树

目录 前言&#xff1a; 树&#xff1a; 树结点之间的关系描述&#xff1a; 树的常见属性&#xff1a; 森林&#xff1a; ​编辑树的性质&#xff1a; 总结&#xff1a; 前言&#xff1a; 当谈论数据结构时&#xff0c;树&#xff08;Tree&#xff09;是一种极为重要且常…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023