目录

前言： 

树：

树结点之间的关系描述：

 树的常见属性：

森林：

​编辑树的性质：

总结：

---

前言： 

当谈论数据结构时，树（Tree）是一种极为重要且常用的数据结构之一。树的概念源自现实生活中的树木，它具有分层结构，由节点（Node）和边（Edge）组成，形成了一种类似于自然界树木生长的结构。在计算机科学领域，树被广泛运用于各种算法和数据存储场景中，如文件系统、数据库索引、编译器等。

 

树：

他的结构就和我们真实的树看起来一样。如下图所示：

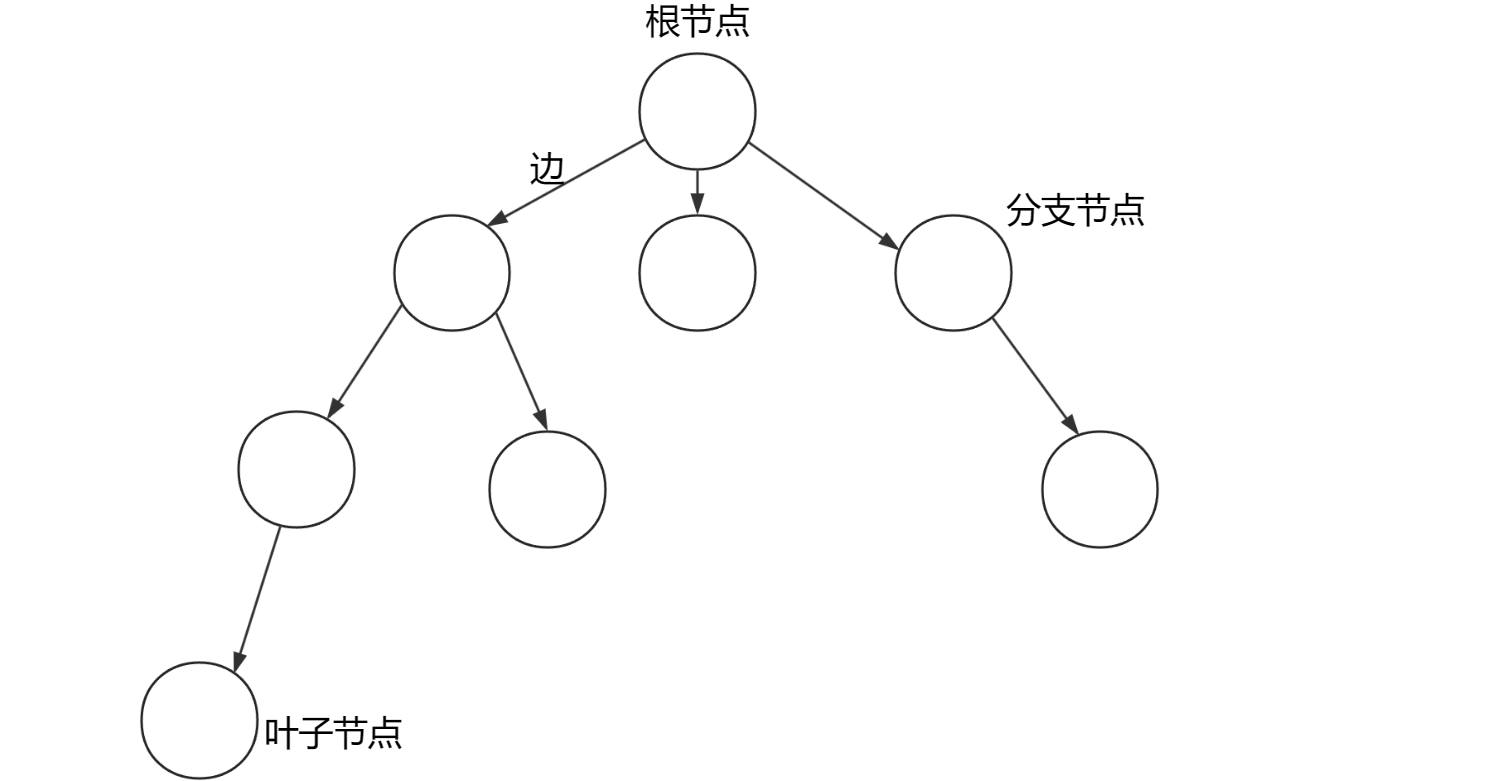
像树这种数据结构，任何节点都有且只有一个前驱。任何一个树都可以看作是由一个根节点以及部分子树构成的。

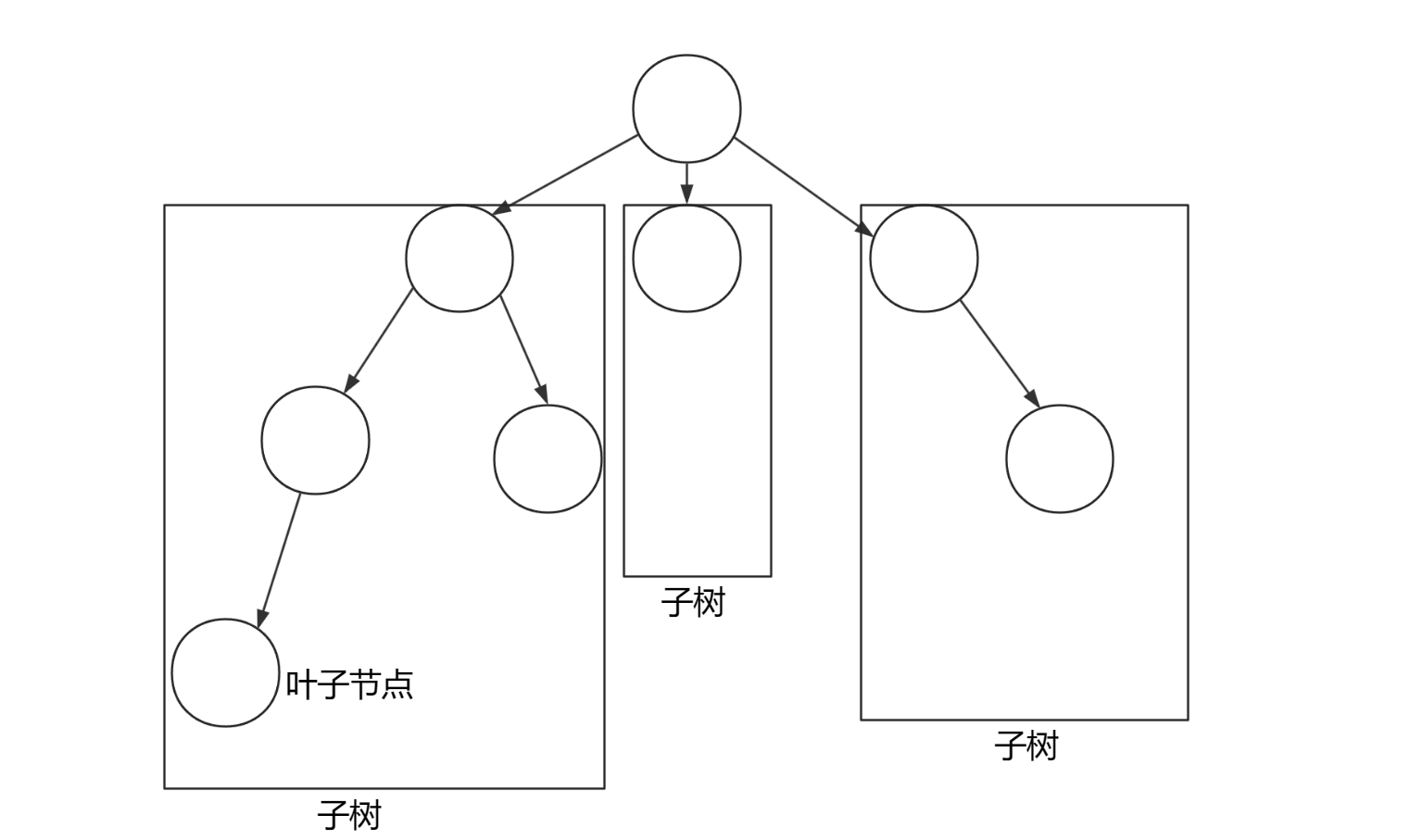
树结点之间的关系描述：

1. 父子关系：树中每个节点（除了根节点）都有一个父节点，父节点指向其子节点，子节点是父节点的直接下级。

2. 兄弟关系：具有同一个父节点的节点之间称为兄弟节点，它们在同一层级上。

3. 祖先和后代关系：一个节点的所有父节点以及这些父节点的父节点等都被称为该节点的祖先；而一个节点的所有子节点以及这些子节点的子节点等都被称为该节点的后代。

4. 叶子节点和内部节点：没有子节点的节点称为叶子节点，而至少有一个子节点的节点称为内部节点。

 树的常见属性：

1. 结点的层次（深度）——从上往下数
2. 结点的高度——从下往上数
3. 树的高度——总共多少层
4. 结点的度——节点一共有几个子节点
5. 树的度——各个节点之中度的最大值

有序树：从逻辑上看：树中结点的各个子树从左至右是有次序的，不能互换。

无序树：从逻辑上看，树中结点的各个子树从左至右是无次序的，可以互换。

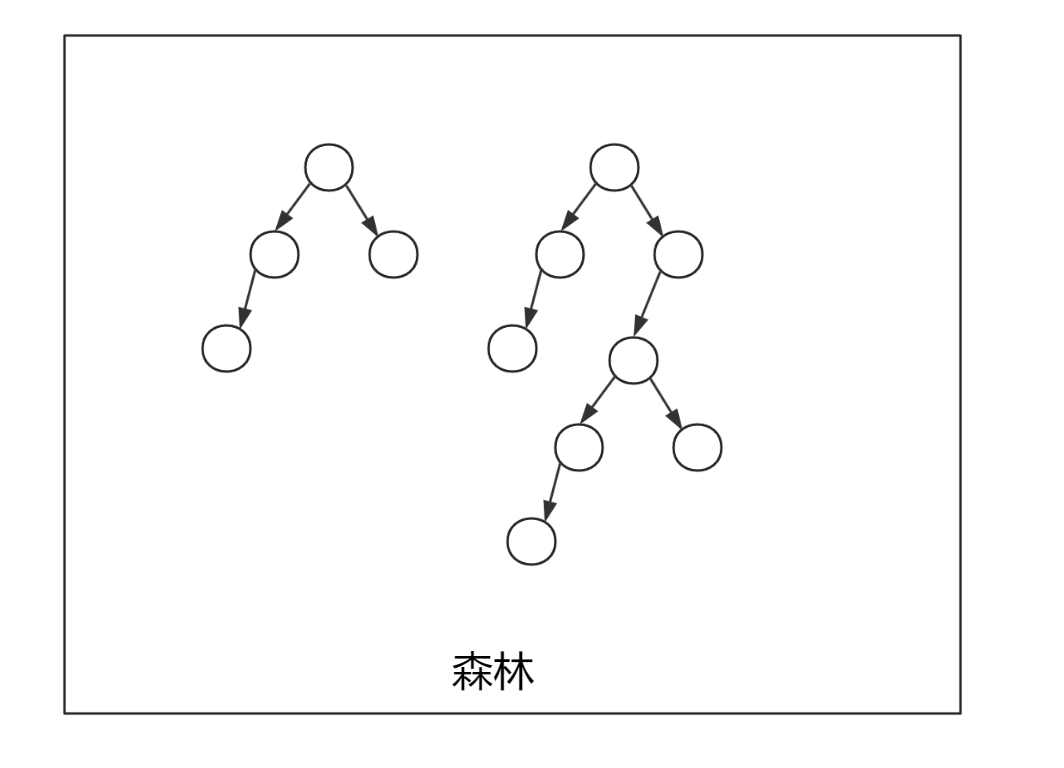
森林：

森林就是多颗互不相交的树的集合

树的性质：

1.结点树=总度数+1

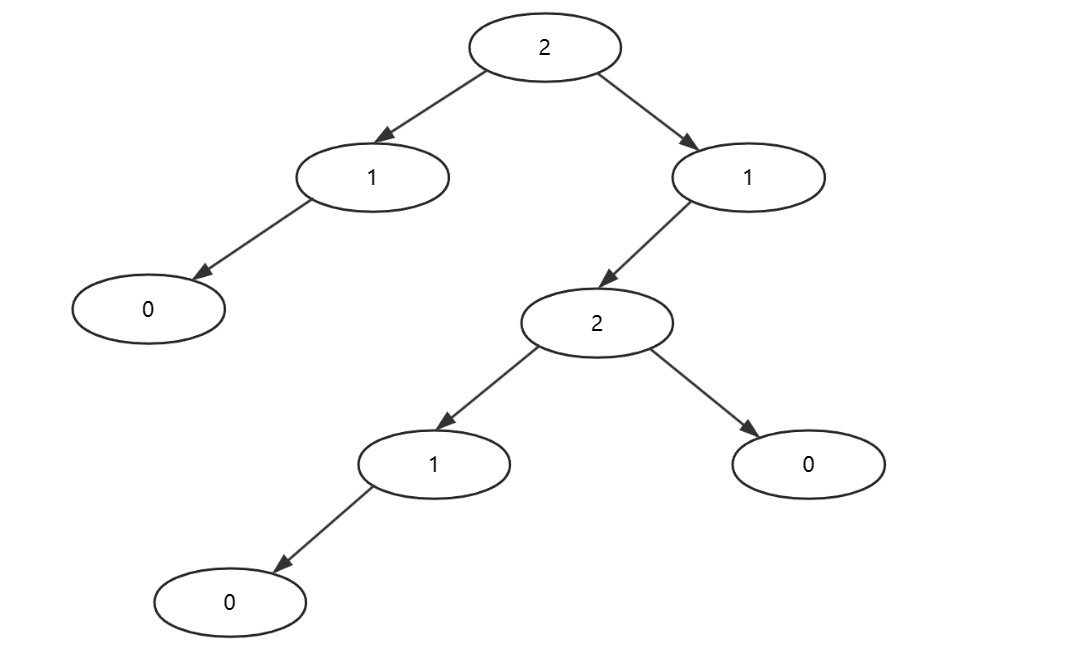
总度数=7，加上1之后等于节点数8。

2.度为m的树与m叉树的区别

度为m的树	m叉树
任意结点的度m(最多有m个子节点)	任意结点的度m
至少有一个结点度=m	允许所有结点的度都<m
一定是非空树，至少有m+1个结点	可以是空树

度为m的树：各节点的度的最大值为m

m叉树：每个节点最多只能有m个子节点的树 

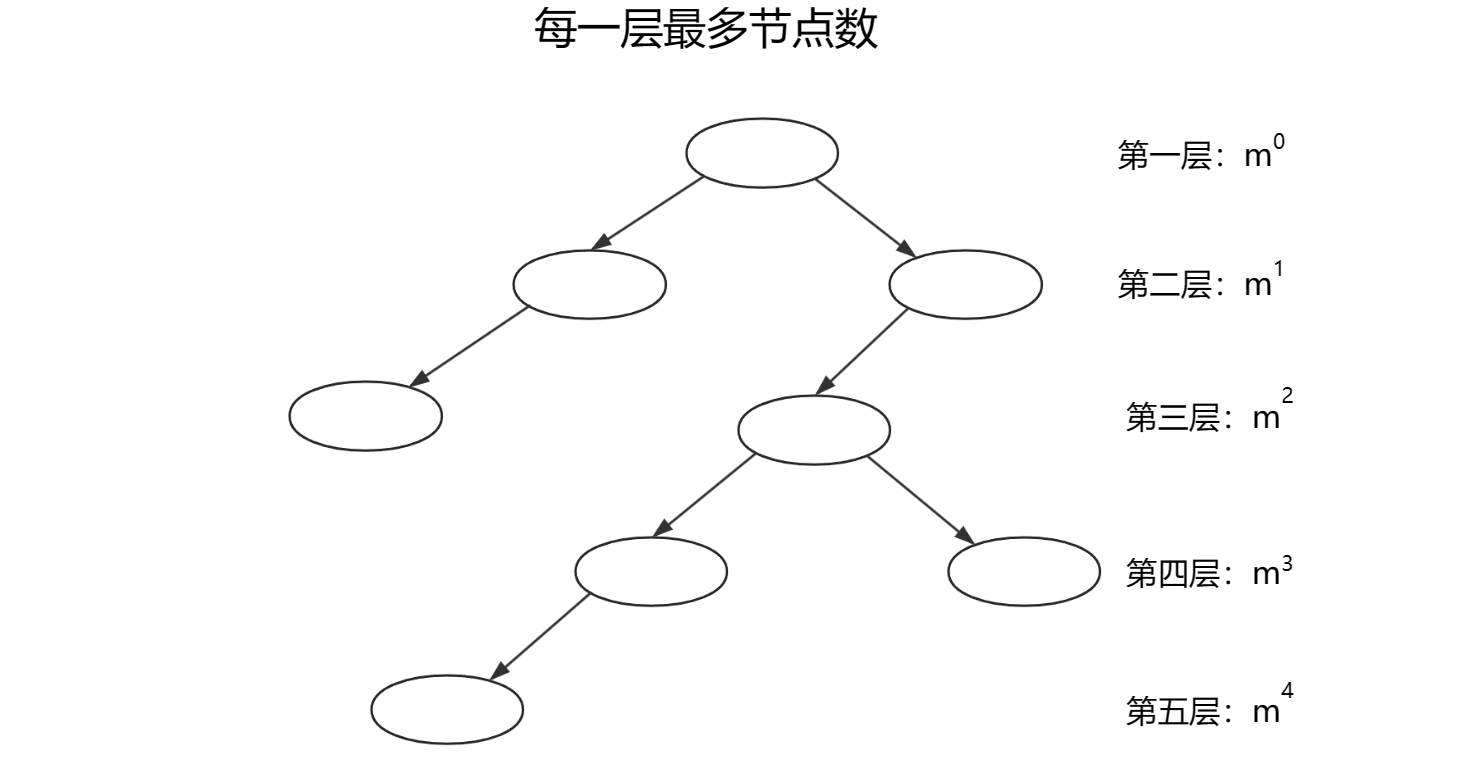
3.度为m的树第i层最多有个节点（i1）

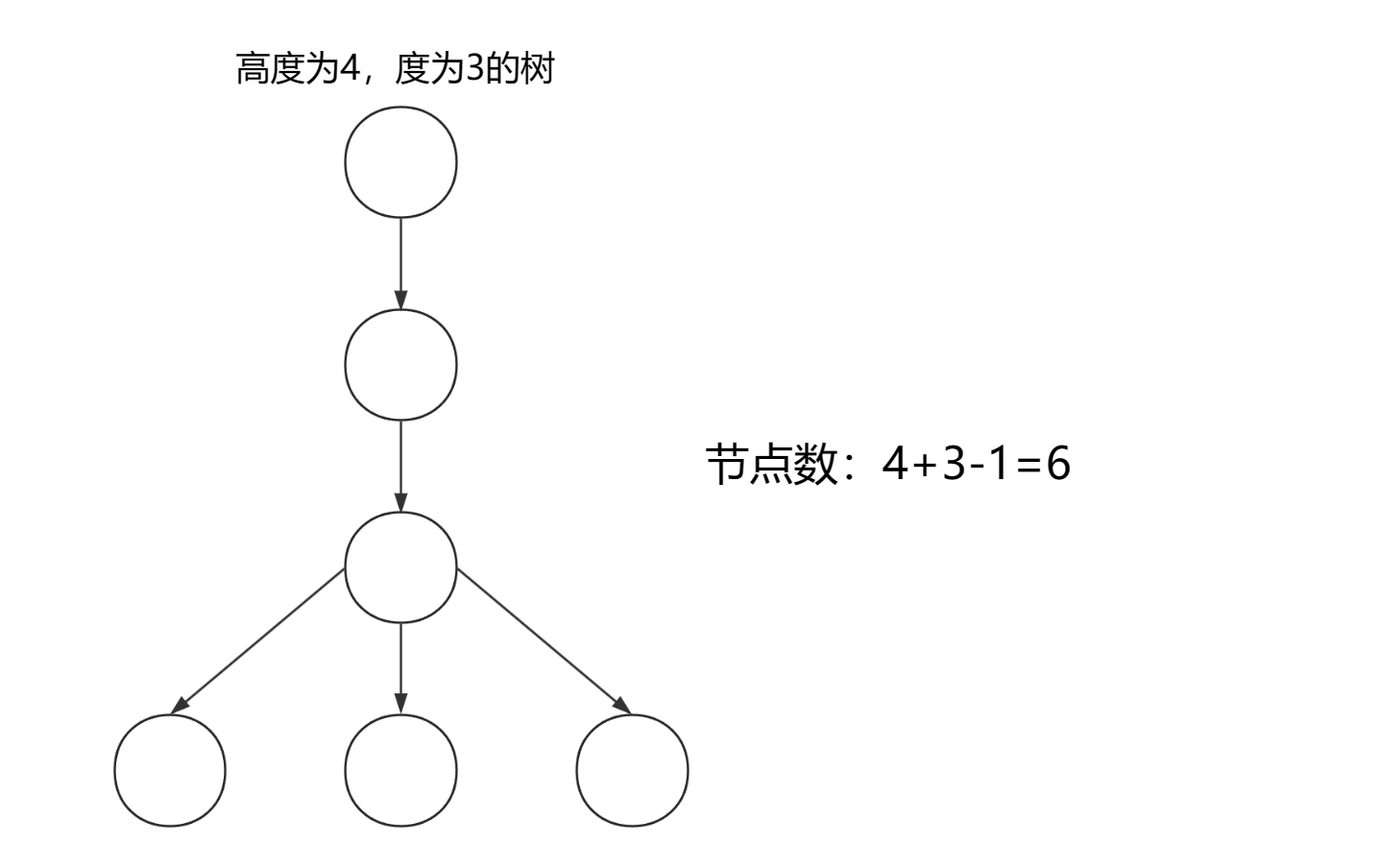
4.高度为h的m叉树最多有 个节点，最少有h个节点

5.高度为h，度为m的树至少有h+m-1个节点。

 6.具有n个节点的m叉树的最小高度为

这其实是用数学推过来的，大家感兴趣的话可以自己推一下。 

总结：

本文我们介绍了一下树以及树的常见性质，下文我们讲深入学习树中一个比较重要的部分：二叉树。

如果我的内容对你有帮助，请点赞，评论，收藏。创作不易，大家的支持就是我坚持下去的动力！