目录

选择题

编程题

不用加减乘除做加法

找到所有数组中消失的数字

---

选择题

1、求函数返回值，传入-1，则在64位机器上函数返回

int func(int x)
{
    int count = 0;
    while (x)
    {
        count++;
        x = x&(x - 1);//与运算
    }
    return count;
}

• A 死循环
• B 64
• C 32
• D 16

答案：C

2、读代码选结果

int count = 0;
int x = -1;
while(x)
{
    count++;
    x = x >> 1;
}
printf("%d",count);

• A 1
• B 2
• C 32
• D 死循环，没结果

答案：D

3、下述赋值语句错误的是

• A a = (b = (c = 2 , d = 3))
• B i++
• C a/b = 2
• D a = a < a + 1

答案：C

4、若有int w=1, x=2, y=3, z=4;则条件表达w < x ? w : y < z ? y : z的值是

• A 1
• B 2
• C 3
• D 4

答案：A

5、以下程序运行后的输出结果是

int main()
 {
     int a=1,b=2,m=0,n=0,k;
     k=(n=b<a)&&(m=a);
     printf("%d,%d\n",k,m);
     return 0;
 }

• A 0,0
• B 0,1
• C 1,0
• D 1,1

答案：A

编程题

不用加减乘除做加法

题目链接：不用加减乘除做加法_牛客题霸_牛客网 (nowcoder.com)

写一个函数，求两个整数之和，要求在函数体内不得使用+、-、*、/四则运算符号。

数据范围：两个数都满足−10≤ n≤1000
进阶：空间复杂度 O(1)，时间复杂度 O(1)

思路解析：

在加法过程中，需要考虑到进位和不进位的情况，而&运算符的计算规则可以产生进位，两个数值相与后左移可以获得进位的位置，而和的值则由异或运算符^的计算规则实现，1^0 = 1(1 + 0 = 1), 1 ^ 1 = 0(1 + 1 = 2，配合&运算符的进位值相与10&(1^1) = 2)，当不再产生进位时，代表加和已经完成，此时处理好和即可

参考代码

/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 * 
 * @param num1 int整型 
 * @param num2 int整型 
 * @return int整型
 */
int Add(int num1, int num2 ) {
    int sub = num1;//记录进位
    int sum = num2;//记录求和
    while (sub != 0) {
        int tmp = sub ^ sum;//计算除了进位的部分
        sub = (sum & sub) << 1;//获取进位
        sum = tmp;//更新sum为和
    }
    return sum;
}

找到所有数组中消失的数字

题目链接：448. 找到所有数组中消失的数字 - 力扣（LeetCode）

给你一个含 n 个整数的数组 nums ，其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字，并以数组的形式返回结果。

思路解析：

本题最直观的想法就是使用异或思想，但是考虑到消失的数字可能不止一个或者两个，此时异或思想不再可用

根据题目描述，数组中的数据为n个，而最大值也为n，可以利用这个特点使用哈希直接定址的思想来进行解决，最直接的办法就是创建一个和原数组大小相同的临时数组tmp，根据原数组中数据出现的次数对应tmp数组的下标位置的值+1，原数组遍历完成后，如果tmp数组中下标对应值为0的，则说明该下标为数组中消失的数字，具体思路如下：

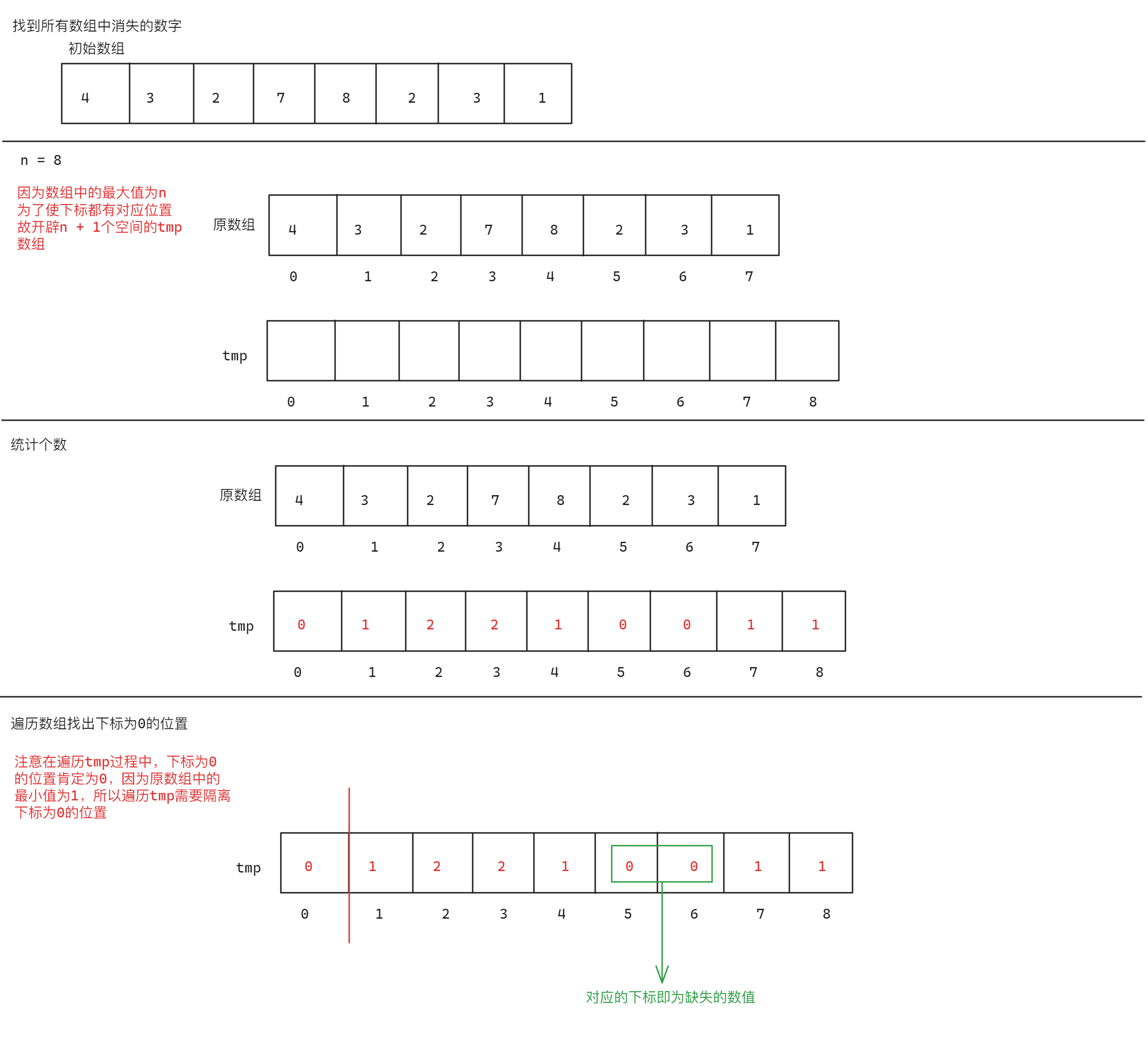
由于额外开辟一个临时数组tmp，所以空间复杂度为O(N)，考虑到题目的特点，数组中最大数值为n，而数组的长度也为n，则此时最后一个元素的下标为n - 1，此时可以考虑套用哈希直接定址的思路在原数组上直接标记，原数组的下标0- (n-1)充当原来的tmp数组的标记位置，具体思路如下：

参考代码：

/*
 * @lc app=leetcode.cn id=448 lang=c
 *
 * [448] 找到所有数组中消失的数字
 */

// @lc code=start
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int *findDisappearedNumbers(int *nums, int numsSize, int *returnSize)
{
    *returnSize = 0;
    int *ans = (int *)malloc(sizeof(int) * numsSize);

    // 计数排序的基本思路——哈希直接定址
    int range = numsSize + 1;
    int *tmp = (int *)calloc(range, sizeof(int));
    for (int i = 0; i < numsSize; i++)
    {
        tmp[nums[i]]++;
    }
    for (int i = 1; i < range; i++)
    {
        if (tmp[i] == 0)
        {
            ans[(*returnSize)++] = i;
        }
    }

    return ans;
}
// @lc code=end

思路优化，空间复杂度由O(N)降低到O(1)

/*
 * @lc app=leetcode.cn id=448 lang=c
 *
 * [448] 找到所有数组中消失的数字
 */

// @lc code=start
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int *findDisappearedNumbers(int *nums, int numsSize, int *returnSize)
{
    int *ans = (int *)malloc(sizeof(int) * numsSize);
    *returnSize = 0;
    for (int i = 0; i < numsSize; i++)
    {
        // 标记数组中的数值，没有被标记为负数的对应的下标+1即为缺失的数值
        // 当遇到已经为负的数值时，不再标记为负
        if (nums[abs(nums[i]) - 1] < 0)
        {
            continue;
        }
        nums[abs(nums[i]) - 1] *= (-1);
    }
    // 遍历数组找出非负值的下标
    for (int i = 0; i < numsSize; i++)
    {
        if (nums[i] > 0)
        {
            ans[(*returnSize)++] = i + 1;
        }
    }
    return ans;
}
// @lc code=end