『GROI-R1』 一切都已过去
题目背景
悦关上窗,拉上帘布。
果然还是想不起来啊。
隐约记得曾和什么人一起做过这样的事。
仰面躺下,手执一只木笺。
「究竟如何,才能拥有“过去”啊……」
她闭上双眼。
「6 岁前的记忆……究竟如何才能寻回?」
题目描述
悦正在寻找她的记忆。忽然,她来到了有 n n n 个节点的一棵树上。树上每一条边都有各自边权,每一个点都有各自的点权。
「把经历都聚拢起来,能完整地复原吗……」
悦从树上的一个点,慢慢地走到了另一个点,可是她什么也没找到。但是,她不知道,玘一直在远处望着她走过的道路。
玘发现,悦全程没有走回头路。他想把悦走过的每一条边的边权乘起来,可惜他发现他遇到了一个这一生未曾见到过的数字。
「为什么会这样呢?」
玘想到悦是突然出现在树上的,最初的点一定有蹊跷!他把最初那个点的点权乘上……
突然,一束彼岸花的红光亮起!世界重新安静了下来。
悦看到了玘留下的字样,可惜她不能从中看出任何过去的记忆。现在,你要帮她判断:把经历都聚拢起来,能完整地复原过去吗?我们称悦的一条路径能“复原过去”,当且仅当玘留下的乘积是一个整数。
形式化题面
给定一棵 n n n 个节点的树和 q q q 次询问。每次询问给出两个整数 x , y x,y x,y,表示询问树上以 x x x 和 y y y 为端点的简单路径上边权乘积与点 x x x 的点权相乘是否为整数。
输入格式
第一行两个正整数 n n n 和 q q q,表示树上有 n n n 个节点编号为 1 ∼ n 1\sim n 1∼n,悦在树上走了 q q q 条路径。
接下来一行 n n n 个非负整数表示每个点的点权 a i a_i ai。
接下来 n − 1 n-1 n−1 行每行两个正整数 u , v u,v u,v 和一个非负实数 w w w 表示 u , v u,v u,v 间有一条边权为 w w w 的边。
接下来 q q q 行,每行两个正整数 x , y x,y x,y,表示悦从点 x x x 开始走到了点 y y y。
输出格式
对于悦的每一次询问,你需要输出一行一个字符串。如果悦能够成功复原她的过去,请输出 Yes,否则请输出 No。
样例 #1
样例输入 #1
5 3
1 2 3 4 5
1 2 0.1
2 3 0.20
3 4 0.5
2 5 0.99
1 5
1 4
4 3
样例输出 #1
No
No
Yes
提示
样例解释
根据输入可以得到下图:
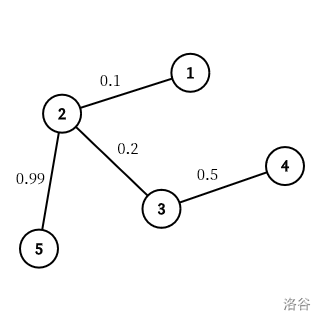
对于第一个询问
(
1
,
5
)
(1,5)
(1,5) 可以发现悦经过的边的边权分别是
0.1
0.1
0.1 和
0.99
0.99
0.99,她出发的
1
1
1 号点的点权为
1
1
1。
1
×
0.1
×
0.99
=
0.099
1\times0.1\times0.99=0.099
1×0.1×0.99=0.099 不是整数。所以输出 No。
对于后面两次询问同理。
数据范围
本题采用捆绑测试。
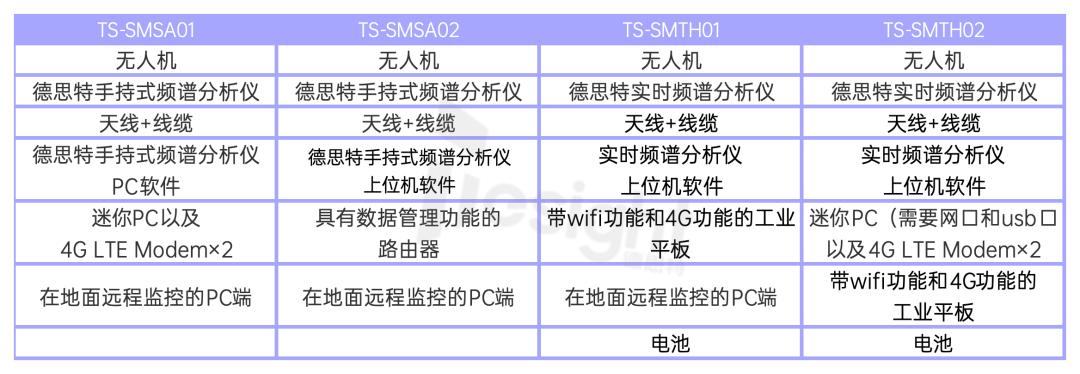
| 子任务编号 | 数据范围 | 特殊性质 | 分值 |
|---|---|---|---|
| Subtask1 \text{Subtask1} Subtask1 | n , q ≤ 3 × 1 0 3 n,q\le3\times 10^3 n,q≤3×103 | 15 15 15 | |
| Subtask2 \text{Subtask2} Subtask2 | n ≤ 500 n\le500 n≤500, q ≤ 1 0 5 q\le10^5 q≤105 | 10 10 10 | |
| Subtask3 \text{Subtask3} Subtask3 | n , q ≤ 1 0 5 n,q\le10^5 n,q≤105 | BE \text{BE} BE | 10 10 10 |
| Subtask4 \text{Subtask4} Subtask4 | n , q ≤ 1 0 5 n,q\le10^5 n,q≤105 | A \text{A} A | 5 5 5 |
| Subtask5 \text{Subtask5} Subtask5 | n , q ≤ 1 0 5 n,q\le10^5 n,q≤105 | B \text{B} B | 10 10 10 |
| Subtask6 \text{Subtask6} Subtask6 | n , q ≤ 1 0 5 n,q\le10^5 n,q≤105 | C \text{C} C | 5 5 5 |
| Subtask7 \text{Subtask7} Subtask7 | n , q ≤ 1 0 5 n,q\le10^5 n,q≤105 | D \text{D} D | 10 10 10 |
| Subtask8 \text{Subtask8} Subtask8 | n , q ≤ 2 × 1 0 5 n,q\le2×10^5 n,q≤2×105 | 35 35 35 |
特殊性质 A \text{A} A:保证树退化成一条链。
特殊性质 B \text{B} B:保证树随机生成(即对于每一个节点随机选择它的父亲节点)。
特殊性质 C \text{C} C:保证 w ∈ { 0.1 , 0.3 , 0.5 , 0.7 , 0.9 } w\in\{0.1,0.3,0.5,0.7,0.9\} w∈{0.1,0.3,0.5,0.7,0.9}。
特殊性质 D \text{D} D:保证 w ∈ { 0.1 , 0.2 , 0.3 , 0.4 , 0.6 , 0.7 , 0.8 , 0.9 } w\in\{0.1,0.2,0.3,0.4,0.6,0.7,0.8,0.9\} w∈{0.1,0.2,0.3,0.4,0.6,0.7,0.8,0.9}。
特殊性质 E \text{E} E:保证 w ≤ 2 w\le2 w≤2 且 w w w 小数位数不超过 1 1 1 位。
对于 100 % 100\% 100% 的数据满足 1 ≤ n , q ≤ 2 × 1 0 5 1\le n,q\le2\times10^5 1≤n,q≤2×105, 0 ≤ a i ≤ 1 0 9 0\le a_i\le10^9 0≤ai≤109, 0 ≤ w ≤ 1 0 4 0\le w\le10^4 0≤w≤104, 1 ≤ u , v , x , y ≤ n 1\le u,v,x,y\le n 1≤u,v,x,y≤n, x ≠ y x\ne y x=y, w w w 小数位数不超过 4 4 4 位。
涉及知识:树上前缀和(LCA),运算符重载。
思路:对于树上两节点间距离或者权值和之类的问题很容易想到树上前缀和的思路,但是按照表面意思进行前缀和之间的乘法的话精度完全不够所以需要转换一下思维,为了让一个小数转换成整数,我们可以枚举一下看看。
得到的可以完成整数转换的其实只有一类:
//0.5*2 -> 0.1 * 5 * 2 --
//0.2*5 -> 0.1 * 5 * 2 ---> 0.1 * 10
//0.4*2.5 -> 0.01 * 5^2 * 2^2 ---> 0.01 * 10^2
因此,只需要统计一下2和5的次幂数以及所有小数点后位数之和,那么2和5组成的是的次幂数即
n
u
m
10
=
m
i
n
(
n
u
m
2
,
n
u
m
5
)
num_{10} = min(num_2,num_5)
num10=min(num2,num5) 。并比较其与小数点后位数之和的大小即得答案。
其中有两个坑点:
如果你的代码TLE了,可能是因为你没有考虑点权为0的情况。
如果你的代码WA了,可能是以为你没有考虑边权出现0的情况。
因此我们只需要特判一下以上两种情况就差不多解决这个问题了。
#include <bits/stdc++.h>
using namespace std;
#define all(x) x.begin(), x.end()
#define bit1(x) __builtin_popcount(x)
#define Pqueue priority_queue
#define lc p << 1
#define rc p << 1 | 1
#define IOS ios::sync_with_stdio(false), cin.tie(0);
#define fi first
#define se second
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
typedef pair<ll, ll> PII;
const ll mod = 1000000007;
const ll N = 1e6 + 10;
const ld eps = 1e-9;
const ll inf = 1e18;
const ll P = 131;
const ll dir[8][2] = {1, 0, 0, 1, -1, 0, 0, -1, 1, 1, 1, -1, -1, 1, -1, -1};
struct node
{
int a, b, c;
} g[N];//定义一个结构体a,b,c依次对应小数点后位数、2的次幂数、5的次幂数
//即由1到第i个节点的树上前缀和
node operator*(node a, int b)
{
return node({a.a * b, a.b * b, a.c * b});
}//重载运算符 *
node operator+(node a, node b)
{
return node({a.a + b.a, a.b + b.b, a.c + b.c});
}//重载运算符 +
node operator-(node a, node b)
{
return node({a.a - b.a, a.b - b.b, a.c - b.c});
}//重载运算符 -
ostream &operator<<(ostream &out, node a)
{
out << a.a << " " << a.b << " " << a.c << "\n";
return out;
}//重载运算符 << (用于Debug)
node check(double x)
{
node tmp({0, 0, 0});
if (x == 0)
return tmp;
while (x != (ll)x)
{
x *= 10;
tmp.a++;
}//取小数点后位数
ll t = x;
while (t % 2 == 0)
{
t /= 2;
tmp.b++;
}//取2的次幂数
while (t % 5 == 0)
{
t /= 5;
tmp.c++;
}//取5的次幂数
return tmp;
}//返回一个实数x包含的node信息
int fa[N][21];//父节点数组i的第2^j位父亲
int dep[N]; //深度数组
int Log2[N + 10];//预处理Log2数组
int zero[N]; //0的树上前缀和数组,由1到第i个节点路径上0的个数
int n, m, u, v;
double w;
vector<pair<int, double>> G[N]; //邻接表存图
void Dfs(int u, int f) //DFS求LCA并构建树上前缀和
{
dep[u] = dep[f] + 1; //求深度
fa[u][0] = f; //u的第一个父亲是f
for (int i = 1; i <= Log2[dep[u]]; i++)
fa[u][i] = fa[fa[u][i - 1]][i - 1];
//u的第2^i个父亲是 (u的第2^{i-1}个父亲) 的第 2^{i-1} 个父亲
for (auto [v, w] : G[u]) //遍历子节点
{
if (v == f)
continue;
zero[v] = zero[u] + (w==0); //统计0的个数
g[v] = g[u] + check(w); //统计其他树上前缀和
Dfs(v, u);
}
}
int Lca(int a, int b) //倍增法求LCA
{
if (dep[a] > dep[b])
swap(a, b);
while (dep[a] != dep[b])
b = fa[b][Log2[dep[b] - dep[a]]];
if (a == b)
return a;
for (int i = Log2[dep[a]]; i >= 0; i--)
if (fa[a][i] != fa[b][i])
a = fa[a][i], b = fa[b][i];
return fa[a][0];
}
void solve()
{
// node a({1, 2, 3}), b({3, 2, 1});
// cout << a * 2;
// cout << a + b;
// cout << a - b;
cin >> n >> m;
vector<int> val(n + 10);
for (int i = 1; i <= n; i++)
cin >> val[i];
for (int i = 1; i < n; i++)
{
cin >> u >> v >> w;
G[u].push_back({v, w});
G[v].push_back({u, w});
}
Dfs(1, 0);
// for (int i = 1; i <= n; i++)
// cout << g[i];
for (int i = 1; i <= m; i++)
{
cin >> u >> v;
node tmp = g[u] + g[v] - g[Lca(u, v)] * 2 + check(val[u]);
//由 u 到 v 路径上的树上前缀和 + 点权中的信息
// cout << check(cal[u]) << tmp;
int z = zero[u] + zero[v] - zero[Lca(u, v)] * 2;
//0的树上前缀和
if (!val[u] || z > 0 || min(tmp.b, tmp.c) >= tmp.a)
//特判两个坑点
cout << "Yes\n";
else
cout << "No\n";
}
}
int main()
{
Log2[0] = -1;
for (int i = 1; i <= N; i++)
Log2[i] = Log2[i / 2] + 1;//预处理Log2数组
IOS int T = 1;
// cin>>T;
while (T--)
solve();
return 0;
}
/*
oxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxox
x o
o _/_/_/_/ _/ x
x _/ o
o _/_/_/_/ _/ _/_/ _/_/ _/_/_/ _/_/ _/_/_/ _/_/ _/_/_/ _/ _/ _/ x
x _/ _/_/ _/ _/ _/ _/ _/ _/ _/ _/ _/ _/ _/ _/ _/ _/ o
o _/ _/ _/ _/ _/ _/ _/ _/ _/ _/ _/ _/ _/ _/ _/_/ x
x _/ _/ _/_/ _/ _/ _/ _/_/_/ _/_/ _/ _/ _/ _/ _/ o
o _/ _/ _/ x
x _/ _/_/ _/ o
o x
xoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxo
*/