模拟

class Solution {
public:
    int sumOfEncryptedInt(vector<int> &nums) {
        int res = 0;
        for (auto x: nums) {
            string s = to_string(x);
            char ch = *max_element(s.begin(), s.end());
            for (auto &c: s)
                c = ch;
            res += stoi(s);
        }
        return res;
    }
};

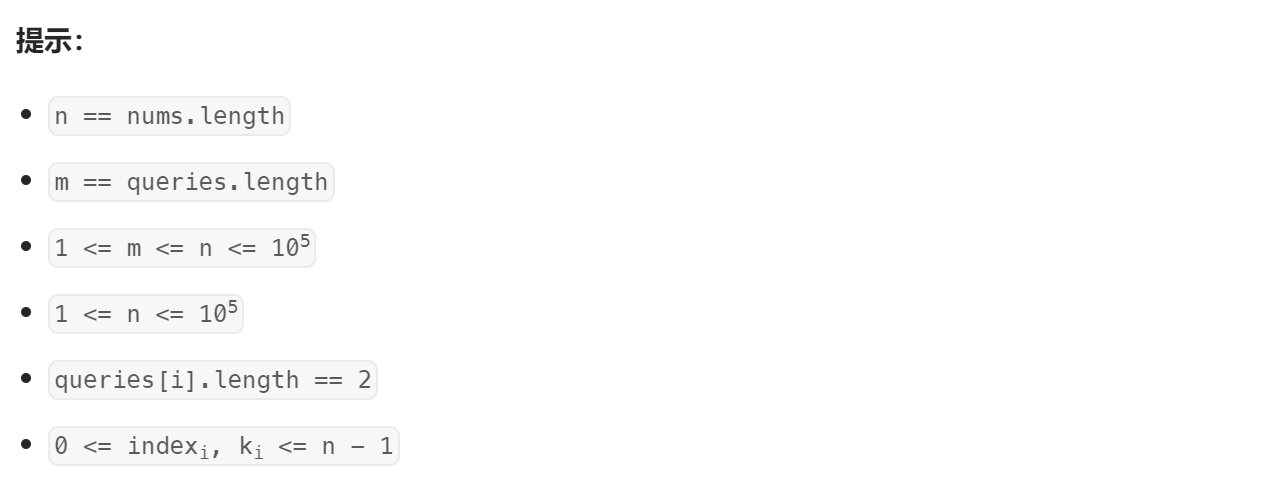
模拟：用堆维护元素中的最小元素，用数组记录元素是否被标记过，模拟对数组的操作过程

class Solution {
public:
    using ll = long long;

    vector<long long> unmarkedSumArray(vector<int> &nums, vector<vector<int>> &queries) {
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> heap;//最小堆
        int n = nums.size();
        for (int i = 0; i < n; i++)
            heap.emplace(nums[i], i);
        ll s = accumulate(nums.begin(), nums.end(), 0LL);
        vector<int> tag(n);
        vector<ll> res;
        for (auto &q: queries) {
            if (!tag[q[0]]) {//未被标记过
                tag[q[0]] = 1;
                s -= nums[q[0]];
            }
            for (int i = 0; i < q[1] && !heap.empty();) {//尽量标记ki个数组中还没有标记的最小元素
                auto [v, ind] = heap.top();
                heap.pop();
                if (tag[ind])
                    continue;
                tag[ind] = 1;
                s -= v;
                i++;
            }
            res.push_back(s);
        }
        return res;
    }
};

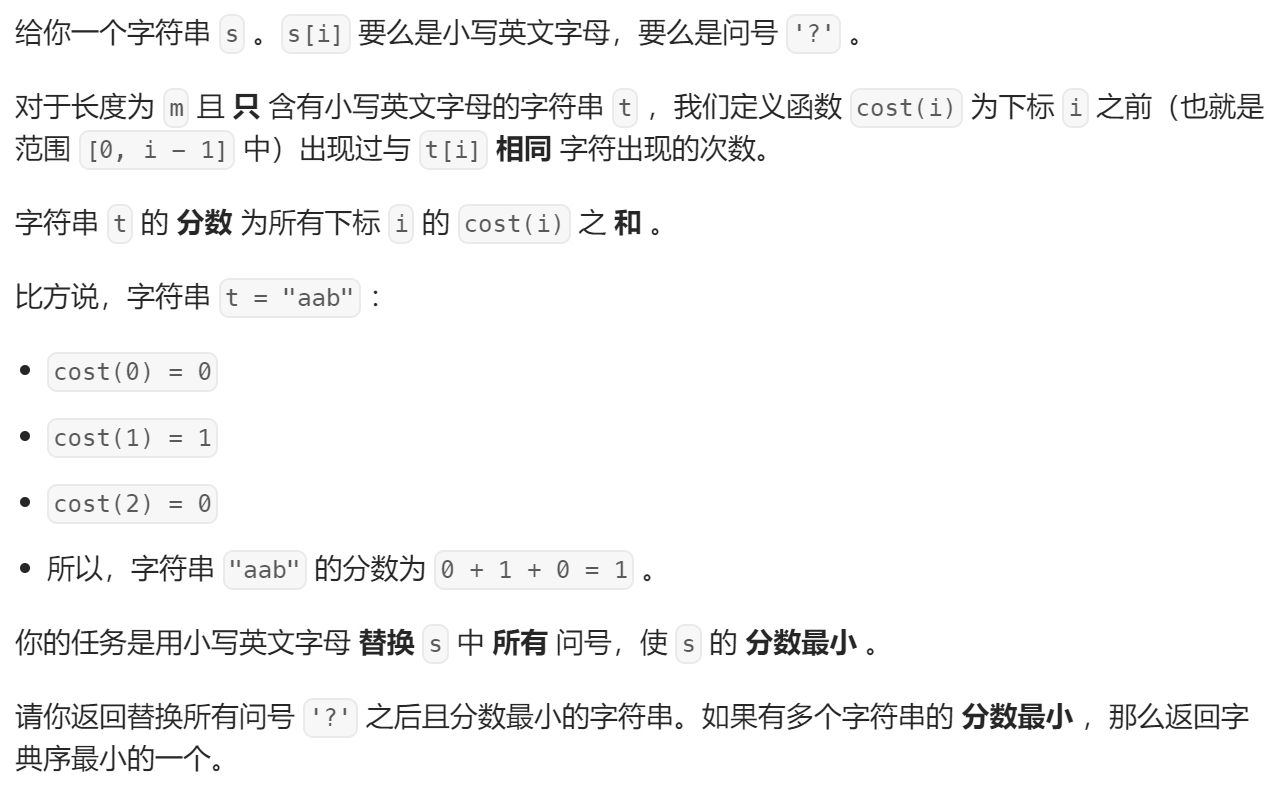
贪心：记录 $s$ 中各英文字母的出现次数，然后遍历 $s$ ,遇到 $?$ 时将当前出现次数最小的英文字母放至该位置，同时该字母出现次数 $+1$ ，最后对原字符串中所有 $?$ 处的字母进行排序，即得到满足条件的字符串

class Solution {
public:
    string minimizeStringValue(string s) {
        vector<int> cnt(26);
        string res;
        vector<char> li;
        vector<int> loc;
        int j = 0;
        for (auto c: s)
            if (c != '?')
                cnt[c - 'a']++;
        for (auto c: s) {
            if (c == '?') {
                int mn = *min_element(cnt.begin(), cnt.end());
                for (int i = 0; i < 26; i++)
                    if (cnt[i] == mn) {
                        cnt[i]++;
                        li.push_back('a' + i);
                        loc.push_back(j);
                        break;
                    }
            }
            j++;
        }
        sort(li.begin(), li.end());
        for (int i = 0; i < li.size(); i++)
            s[loc[i]] = li[i];
        return s;
    }
};

动态规划：设 $p[i+1][j][v]$ 为字符串 $nums[0,i]$ 中长度为 $j$ 和为 $v$ 的自序列的数目，因为 $nums$ 任意一个长为 $j$ 的子序列，$nums$ 包含该子序列的子序列数目为 $2^{n-j}$ ，所以 $nums$ 中所有子序列的能量和为 ${\sum }_{j=1}^{n}p[n][j][k]\times 2^{n-j}$

class Solution {
public:
    using ll = long long;

    int sumOfPower(vector<int> &nums, int k) {
        ll mod = 1e9 + 7;
        int n = nums.size();
        int p[n + 1][n + 1][k + 1];
        memset(p, 0, sizeof(p));
        p[0][0][0] = 1;
        for (int i = 0; i < n; i++) {
            p[i + 1][0][0] = 1;
            for (int j = 1; j <= i + 1; j++)
                for (int v = 1; v <= k; v++) {
                    if (v - nums[i] >= 0)
                        p[i + 1][j][v] = (p[i + 1][j][v] + p[i][j - 1][v - nums[i]]) % mod;
                    p[i + 1][j][v] = (p[i + 1][j][v] + p[i][j][v]) % mod;
                }
        }
        vector<ll> pow(n);
        pow[0] = 1;
        for (int i = 1; i < n; i++)
            pow[i] = pow[i - 1] * 2 % mod;
        ll res = 0;
        for (int j = 1; j <= n; j++)
            if (p[n][j][k])
                res = (res + p[n][j][k] * pow[n - j]) % mod;
        return (res + mod) % mod;
    }
};