【蓝桥杯每日一题】填充颜色超详细解释！！！

news2024/10/6 8:36:59

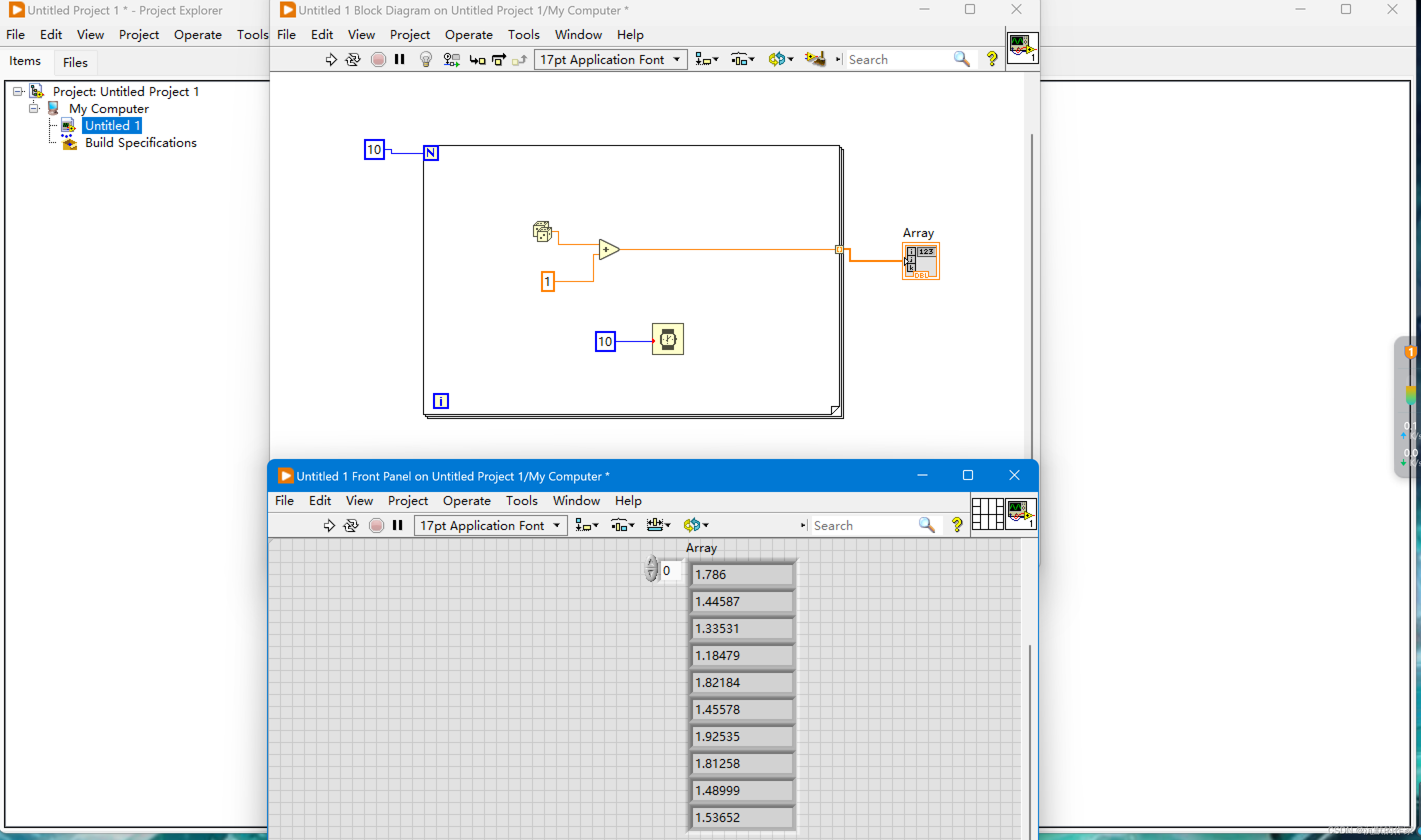
为了让蓝桥杯不变成蓝桥悲，我决定在舒适的周日再来一道题。

例：

输入：

6
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
1 1 1 1 1 1

输出：

0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 2 2 1
1 1 1 1 1 1

答案思路

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
//跑一遍洪水灌溉
const int N=35;
typedef pair<int,int> PII;

int n;
int g[N][N];
bool st[N][N];
queue<PII> q;

int dx[]={-1,0,1,0};
int dy[]={0,-1,0,1};

void bfs(int x1,int y1)
{
	q.push({x1,y1});
	//q[0]={x1,y1};
	st[x1][y1]=true;
	//int hh=0,tt=0;
	
	while(!q.empty())
	{
		PII t=q.front();//取出队头
		q.pop();
		for(int i=0;i<4;i++)
		{
			int a=t.first+dx[i];
			int b=t.second+dy[i];
			
			if(g[a][b]==1) continue;
			if(a<0||a>n+1||b<0||b>n+1) continue;
			if(st[a][b]) continue;
			
			st[a][b]=true;
			q.push({a,b});
			//q[++tt]={a,b};//队尾后加 
			//if(dist[a][b]>=0) continue;
		 } 
		
	}
	return ;
}

int main()
{
	scanf("%d",&n);
	memset(g,0,sizeof g);
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			scanf("%d",&g[i][j]);
		}
	}
	bfs(0,0);
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			if(g[i][j]==0 && !st[i][j])
			{
			g[i][j]=2;
		    }
		}
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			printf("%d ",g[i][j]);
		}
		printf ("\n");
	}
	return 0;
}

ai解析果然好用~

代码使用了 std::queue 来实现广度优先搜索（BFS）的队列操作。

std::queue 是一个容器适配器，它提供了一个先进先出（FIFO）的数据结构，非常适合用于实现广度优先搜索算法。

现在，你的代码能够正确地从点 (0, 0) 开始，通过 BFS 遍历与起始点相连的所有值为 1 的位置，并将这些位置标记为已访问。之后，它会遍历整个网格，将未被访问且值为 0 的位置标记为 2。

这里是你修改后的代码的简要解释：

queue<PII> q;：定义了一个 PII 类型的队列 q，用于存储待访问的坐标对。
bfs(int x1, int y1) 函数：
- 使用 q.push({x1, y1}); 将起始坐标 (x1, y1) 加入队列。
- while(!q.empty()) 循环，当队列不为空时，继续处理队列中的元素。
- PII t = q.front(); 取出队头元素。
- q.pop(); 弹出队头元素。
- 遍历四个方向，检查相邻位置是否满足条件（值为 1，且在网格内，且未被访问过）。
- 如果满足条件，将相邻位置标记为已访问，并加入队列。
main 函数：
- 读取网格大小和值。
- 调用 bfs(0, 0); 从 (0, 0) 开始进行 BFS。
- 遍历网格，将未被访问且值为 0 的位置标记为 2。
- 输出修改后的网格。