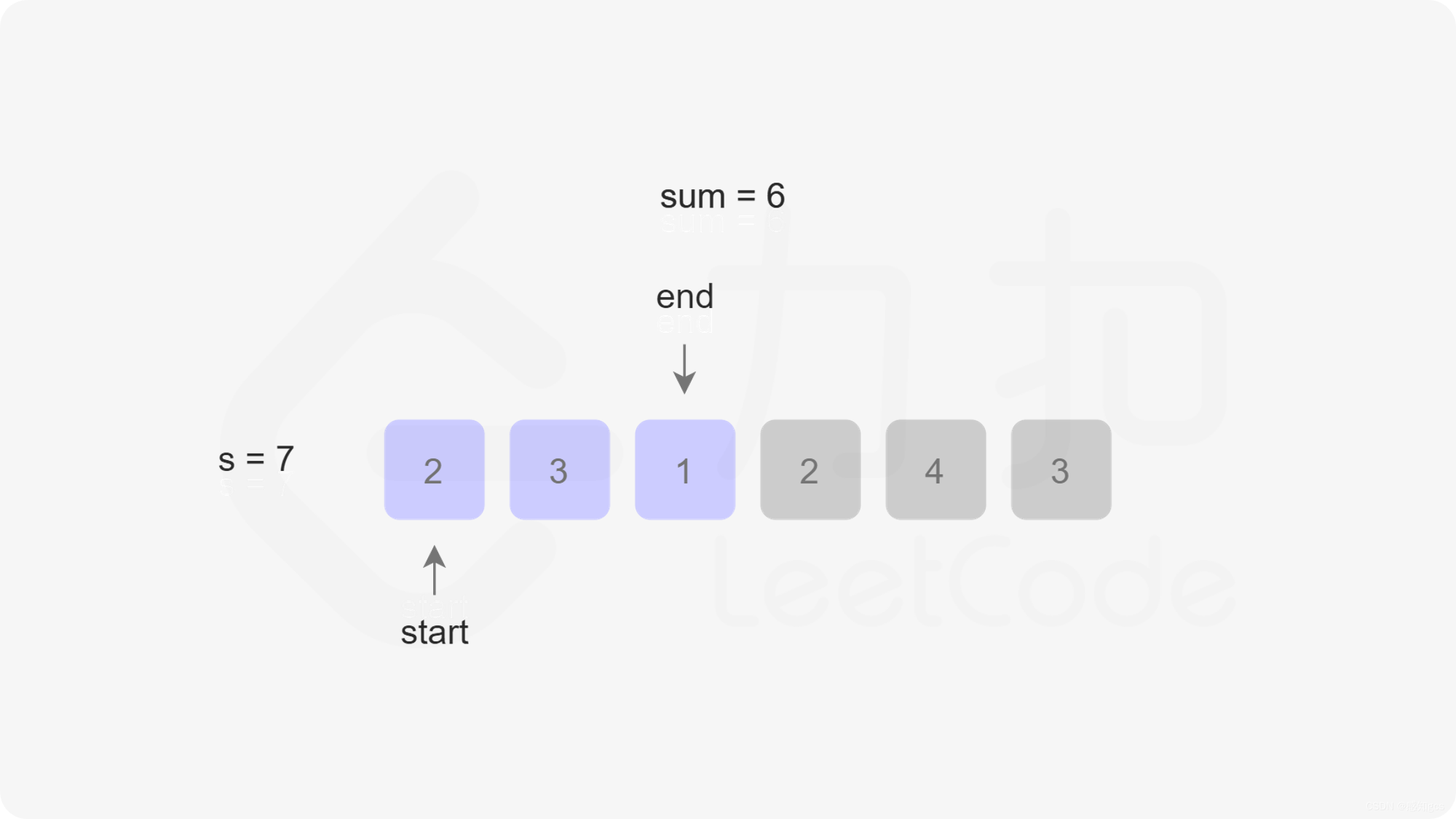
组合总和

     def backtracking2(self, n: int, k: int, startindex: int, targetsum, sum):
         # 递归的终止条件
         if sum > targetsum:
             return
         if len(self.path) == k and sum==targetsum:
             self.result.append(self.path[:])  # 结果拷贝

             return self.result

         # for i in range(startindex,n+1):# 横向处理，在没有剪枝的情况下需要遍历 数组的长度 次
         #     # 单层递归的逻辑：二叉树深度搜索
         #     self.path.append(i)
         #     self.backtracking(n,k,i+1)
         #     self.path.pop()

         # 剪枝优化
         for i in range(startindex, n - (k - len(self.path)) + 2):  # 剪枝处理，i再大，就不满足k个了，就搜不到对应的组合了

             # 单层递归的逻辑：二叉树深度搜索
             self.path.append(i)
             sum += i
             # 如果此时加的元素数量没有超过k，才继续添加，否则直接pop
             if len(self.path)<=k:
                 self.backtracking2(n, k, i + 1,targetsum,sum)
             self.path.pop()  # 回溯处理
             sum -= i

电话号码的组合

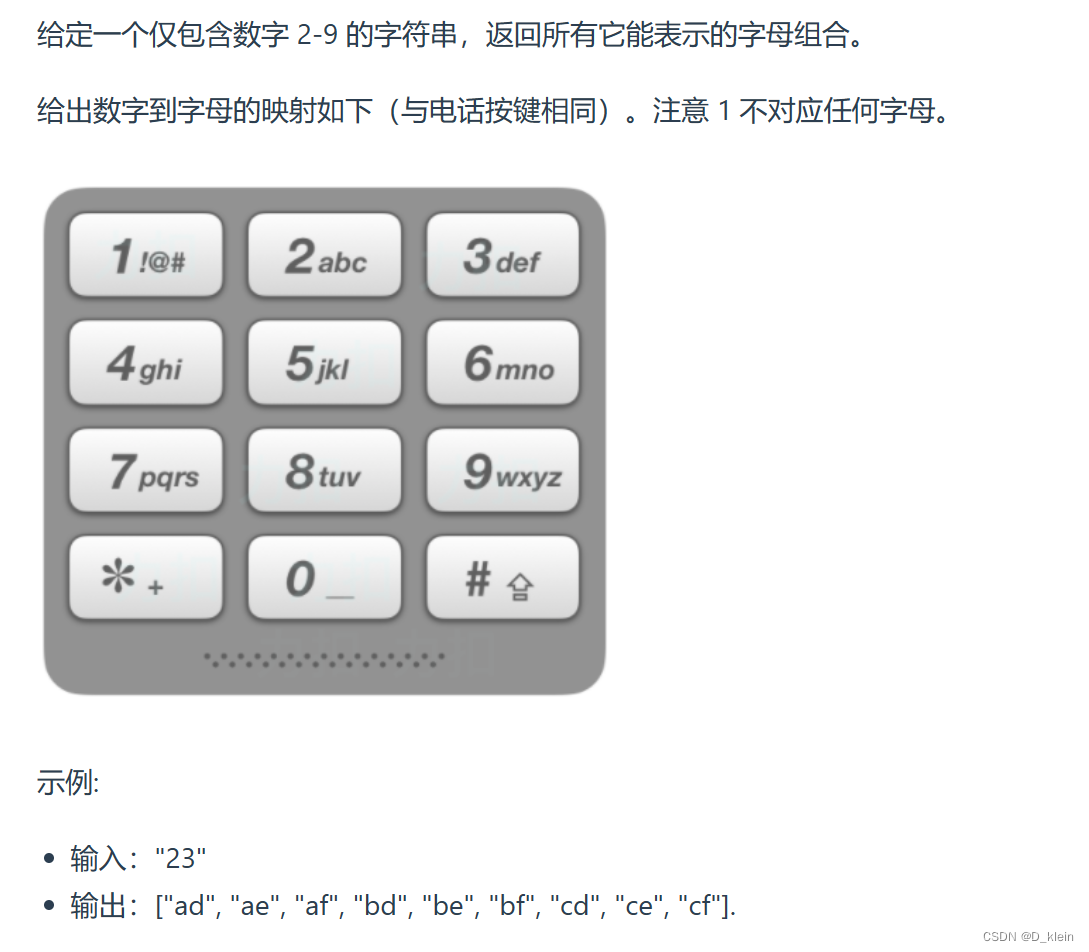
注意：长度即横向遍历为每一个数字对应的电话号码的长度，题目中为3，纵向对应于我们输入的数字的长度，即需要几个数字对应的电话号码的组合，题目中为“23”，所以树的深度为2，在纵向递归的时候，电话号码是不断变化的。

class solution:
    def __init__(self):
        self.letterMap = [
            "",  # 0
            "",  # 1
            "abc",  # 2
            "def",  # 3
            "ghi",  # 4
            "jkl",  # 5
            "mno",  # 6
            "pqrs",  # 7
            "tuv",  # 8
            "wxyz"  # 9
        ]

        self.result=[]
        self.path=[]
    # 参数：需要记录遍历到哪个字母组合,index里包含哪些数字对应的字母组合,k代表树的深度，
    def CombineLetter(self, indexs:str,k):
        if self.path==len(indexs):
            self.result.append(self.path[:])

        index=int(indexs[k]) # 对应到电话号码
        letter=self.letterMap[index] # 电话号码对应的字母
        # # 需要横向遍历的长度，即三次
        for i in range(len(letter)):
            # 递归的深度，树的深度
            self.path.append(letter[i])
            # k是不断变化的
            k+=1
            self.CombineLetter(indexs,k)
            # 回溯
            self.path.pop()
            k-=1