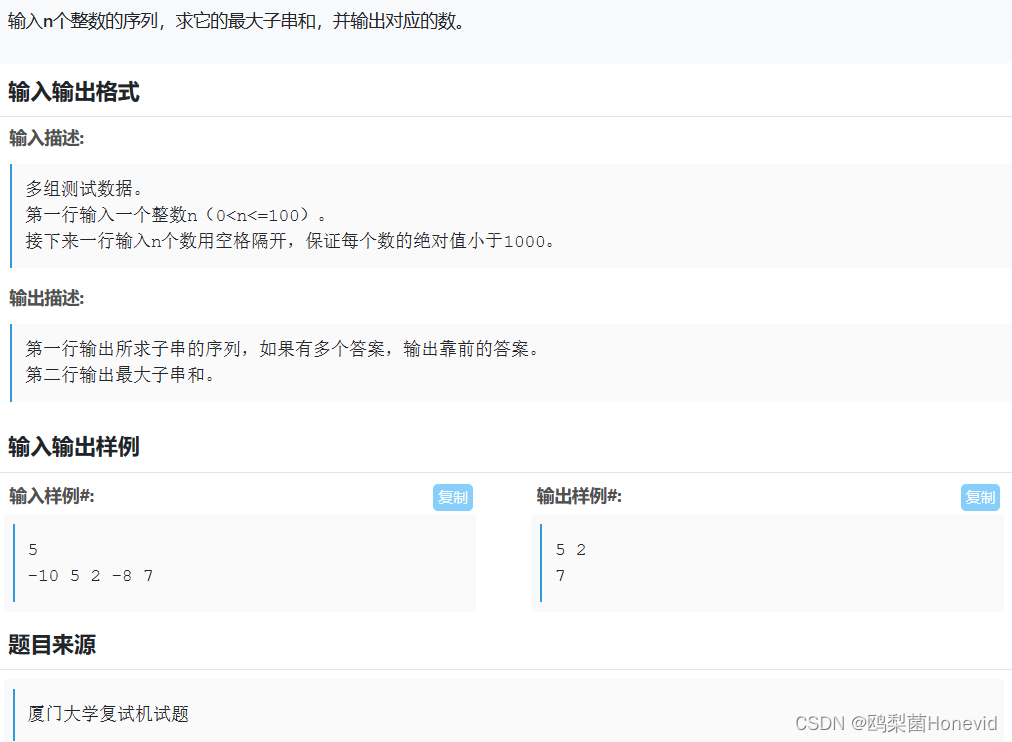
题目

分析——暴力

两个for循环，计算每一种子序（连续）和的值，找到最大时的自序起点和终点，输出即可

代码

#include <cstdio>
#include <map>
#include <string>
#include <cmath>
#include <vector>
#include <algorithm>
#include <stack>
#include <queue>
#include <set>
#include <limits.h>

using namespace std;

int main(){
  int n;
  int seq[101];
  int rut[101];
  int a,b;
  while(scanf("%d",&n)!=EOF){

    for(int i=0;i<n;i++){
      scanf("%d",&seq[i]);
    }

    int max = INT_MIN;
    for(int i=0;i<n;i++){
      int sum = seq[i];
      if(sum>max){
        max = sum;
        a=i;b=i;
      }
      for(int j=i+1;j<n;j++){
        sum += seq[j];
        if(sum>max){
          max = sum;
          a=i;b=j;
        }
      }
    }
    for(int i=a;i<=b;i++){
      printf("%d ",seq[i]);
    }
    printf("\n%d\n",max);
  }
	return 0;
}

分析——贪心

若起点值是负数，下一个值是正数，那么如果仍然从这个负数开始计算，总体值会变小，不如抛弃这个负数，将下一个正数作为起点

• 局部最优：连续和为负数时，选择当前值作为新的起点，重新开始计算，（注意，不是遇到负数就抛弃）
• 全局最优：获得全局最大值

代码

#include <cstdio>
#include <map>
#include <string>
#include <cmath>
#include <vector>
#include <algorithm>
#include <stack>
#include <queue>
#include <set>
#include <limits.h>
using namespace std;

int main(){
  int n;
  int seq[101];
  int a,b;
  while(scanf("%d",&n)!=EOF){

    for(int i=0;i<n;i++){
      scanf("%d",&seq[i]);
    }

    int result = INT_MIN;
    int count = 0;

    for(int i=0;i<n;i++){
      count += seq[i];
      if(count>result){
        result = count;
        b = i;
      }
      if(count<0){
        count = 0;
      }
    }
    int temp = result;
    a = b;
    while(true){
      temp -= seq[a];
      if(temp==0){
        break;
      }
      a--;
    }
    for(int i=a;i<=b;i++){
      printf("%d ",seq[i]);
    }
    printf("\n%d\n",result);
  }
	return 0;
}

分析——动态规划

求最大子序和

1. dp数组的含义：以$num[i]$为结尾的最大子序列之和
2. 递推公式：$dp[i]=max(dp[i-1]+num[i],num[i])$
   • 与前面的子串和累加：$=dp[i-1]+num[i]$
   • 抛弃前面的子串：$=num[i]$
3. dp数组初始化，$dp[0]=num[0]$
4. 遍历顺序：从1到末尾（n-1）
5. 最终结果：dp数组中最大的值

求最大子序的始末位置

求法其实跟上面的贪心一样，上面忘了说，这里补充一下始末位置的求法：
a是起始序号，b是结束序号，temp是最大子序和result的copy

1. 找到最大子序串结束的位置b，令a=b
2. while(true)：temp减去seq[a]的值，然后判断是否为0，如果为零结束循环，不为零就让a自减1
3. 上面的while结束就能得到a，就是起始序号

代码

#include <cstdio>
#include <map>
#include <string>
#include <cmath>
#include <vector>
#include <algorithm>
#include <stack>
#include <queue>
#include <set>
#include <limits.h>
using namespace std;

int main(){
  int n;
  int seq[101];
  int dp[101];
  int a,b;
  while(scanf("%d",&n)!=EOF){
    //输入
    for(int i=0;i<n;i++){
      scanf("%d",&seq[i]);
    }
    //dp数组初始化
    dp[0]=seq[0];
    //开始遍历
    for(int i=1;i<n;i++){
      dp[i]=max(dp[i-1]+seq[i],seq[i]);
    }
    int temp = dp[0];
    for(int i=1;i<n;i++){
      if(temp<dp[i]){
        temp = dp[i];
        b=i;
      }
    }
    a=b;
    int result = temp;
    while(true){
      temp -= seq[a];
      if(temp==0){
        break;
      }
      a--;
    }
    for(int i=a;i<=b;i++){
      printf("%d ",seq[i]);
    }
    printf("\n%d\n",result);
  }
	return 0;
}