【题目描述】

小明最近迷上了积木画，有这么两种类型的积木，分别为 I 型（大小为 2 个单位面积）和 L 型（大小为 3 个单位面积）：

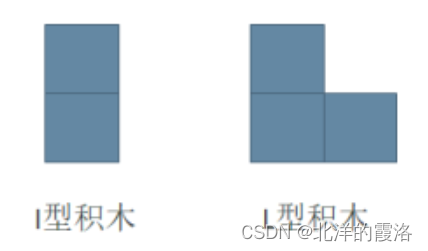
同时，小明有一块面积大小为 2×N 的画布，画布由 2×N 个 1×1 区域构成。

小明需要用以上两种积木将画布拼满，他想知道总共有多少种不同的方式？

积木可以任意旋转，且画布的方向固定。

【输入格式】

输入一个整数 N，表示画布大小。

【输出格式】

输出一个整数表示答案。

由于答案可能很大，所以输出其对 1000000007 取模后的值。

【数据范围】

1≤N≤10的7次方

【输入样例】

3

【输出样例】

5

【样例解释】

五种情况如下图所示，颜色只是为了标识不同的积木：

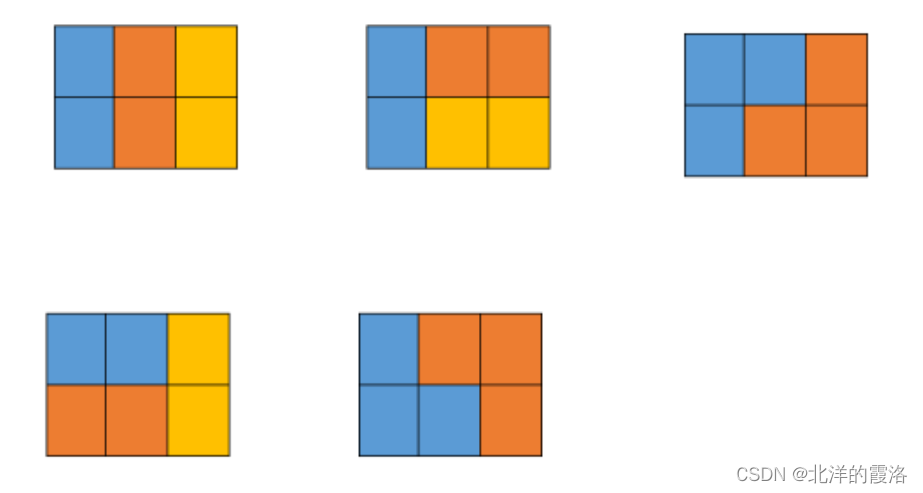
【代码】

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e7 + 10, MOD = 1e9 + 7;

int n;
int g[4][4] = {
    {1, 1, 1, 1},
    {0, 0, 1, 1},
    {0, 1, 0, 1},
    {1, 0, 0, 0},
};
int f[2][4];

int main()
{
    scanf("%d", &n);
    f[1][0] = 1;

    for (int i = 1; i <= n; i ++ )
    {
        memset(f[i + 1 & 1], 0, sizeof f[0]);
        for (int j = 0; j < 4; j ++ )
            for (int k = 0; k < 4; k ++ )
                f[i + 1 & 1][k] = (f[i + 1 & 1][k] + f[i & 1][j] * g[j][k]) % MOD;
    }

    printf("%d\n", f[n + 1 & 1][0]);
    return 0;
}