目录

1解题思路:首先二分查找分为左闭右闭和左闭右开两种情况，二种情况在细节处理上有所不同                                        

 2左闭右闭情况

 3左闭右开

 4总结：

---

 

1解题思路:首先二分查找分为左闭右闭和左闭右开两种情况，二种情况在细节处理上有所不同                                        

 2左闭右闭情况

注意while条件为left<=right,别忘记等号，因为目标值可能会出现在right==left的位置。

int search(int nums[], int size, int target)
{
	int left = 0;
	int right = size; 
	while (left <= right) {	//条件left < right 修改为 left <= right
		int middle = left + ((right - left) / 2);
		if (nums[middle] > target) {
			right = middle; 
		} else if (nums[middle] < target) {
			left = middle + 1;
		} else {
			return middle;
		}
	} 
    // 没找到就返回-1
	return -1;
}

 3左闭右开

这种情况下的循环条件为left<right，不能加=，

代码：

int search(int nums[], int size, int target)
{
	int left = 0;
	int right = size; //定义target在左闭右开的区间里，即[left, right)
	while (left < right) {	//因为left = right的时候，在[left, right)区间上无意义
		int middle = left + ((right - left) / 2);
		if (nums[middle] > target) {
			right = middle; //target 在左区间，在[left, middle)中 
		} else if (nums[middle] < target) {
			left = middle + 1;
		} else {
			return middle;
		}
	} 
    // 没找到就返回-1
	return -1;
}

 4总结：

二分法最重要的两个点，就是循环条件和后续的区间赋值问题；

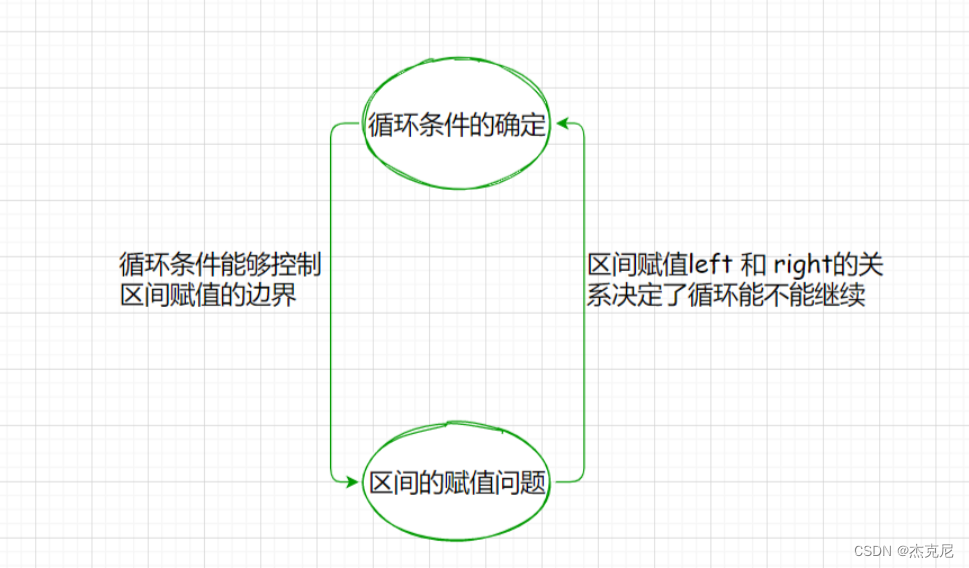
因为两者是相互联系，相互影响的，所以就需要两者统一，如果两者不统一，就会出现问题

所以循环条件和赋值问题必须统一，也就是循环不变量。