计算机系统·浮点数

news2025/1/17 6:06:21

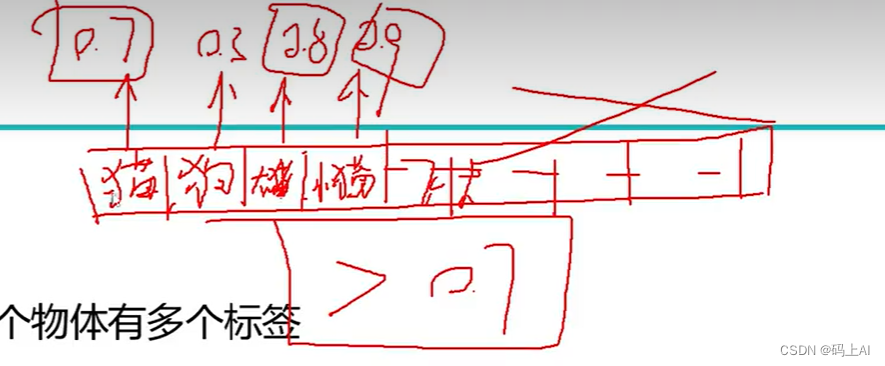
浮点数

理解含有小数值的二进制数

定点表示方法

十进制：以小数点为分界线，小数点左边数字的权重是10的正幂，小数点右边数字的权重是10的负幂。如图所示
在这里插入图片描述
二进制：小数点左边数字的权重是2的正幂，小数点右边数字的权重是2的负幂。如图所示，倒数第二位应为 $b_{-n+1}$

缺点：无法表示非常大的数

IEEE浮点数表示

公式： $V = (-1)^{s} * M * 2^{E}$
以单精度浮点数为例来理解二进制位与浮点数的关系
C语言中的float占4个字节，32bits，被划分为三个字段：

s：最高位31位表示符号位，当s=0，表示正数；当s=1，表示负数
exp：从30位到23位，8个二进制位与阶码的值E相关
frac：剩余的23位与位数M相关
具体表示如图所示

double与float相比：阶码E字段的长度为11为，小数字段的长度为52位

浮点数数值分类

规格化的值（Normalized Values）
非规格化的值（Denornalized Values）
特殊值（Special Values）
阶码的值决定了这个数属于哪一类
当阶码字段的二进制不全位0，且不全为1时，此时表示规格化的值
当阶码字段全为0时，表示的数值是非规格化的值
当阶码字段全为1时，表示的数值时特殊值
1. 一类表示无穷大或者无穷小
2. 一类表示不是一个数NaN

浮点数数值的表示

规格化的值

阶码部分

e的取值与8个二进制位有关，取值范围： $1 <= E <= 254$
阶码E的取值不等于e，而是等于e减去一个偏置值bias，即 $E = e - bia s$
偏置量的值与解码字段的位数是相关的：

$bias_{(float)} = 2^{8-1}-1 = 127$
$bias_{(double)} = 2^{11-1}-1 = 1023$
对于单精度浮点数，阶码的最小值是-126，最大值是127

小数字段

尾数M被定义为1+f。二进制表示如图所示
在这里插入图片描述

公式： $M = 1.f_{22}f_{21}......f_{1}f_{0} = 1+f$
因为我们可以调整E的取值，使尾数M的取值范围为 $1 <= M <= 2$ ，既然第一位总是1，那么没有必要显示的表示出来，所以尾数M的值要加1

非规格化的值

当阶码字段的二进制位全为0时，所表示的是非规格化的值
非规格化的数有两个用途：

提供数值0的表示方法
- 当s=0，M=f=0，e=0，此时表示正零
- 当s=1，M=f=0，e=0，此时表示负零
表示非常接近0的数
- 当阶码字段全为0时，价码E的值等于1-bias，尾数的值M等于f，不包含隐藏的1
- 公式:
  - $E = 1 - bia s$
  - $M = f$
- 与规格化的计算不同，如图所示，白色部分是规格化

特殊值

当阶码字段全为1，且小数字段全为0，表示无穷大的数，分为正无穷打大和负无穷大

正无穷大，符号位为0
负无穷大，符号位为1

运算结果不为实数或者用无穷也无法表示的情况
NaN（Not a Number）如： $s q r t (- 1)$
阶码字段全为1，小数字段不为0

浮点数的存储与转换

int转换称float

例子：12345->12345.0
12345的二进制表示为0000 0000 0000 0000 0011 0000 0011 1001，如图所示在这里插入图片描述
由于高18位全为0，所以我们可以忽略高十八位，只关注低十四位
由规格化的表示可知： $12345 = 1.1 0000 0011 1001 * 2^{13}$
根据IEEE的编码规则：将小数点左边1丢弃，由于单精度浮点数的小数字段长度为23，需要在末尾增加十个零，如图所示
在这里插入图片描述