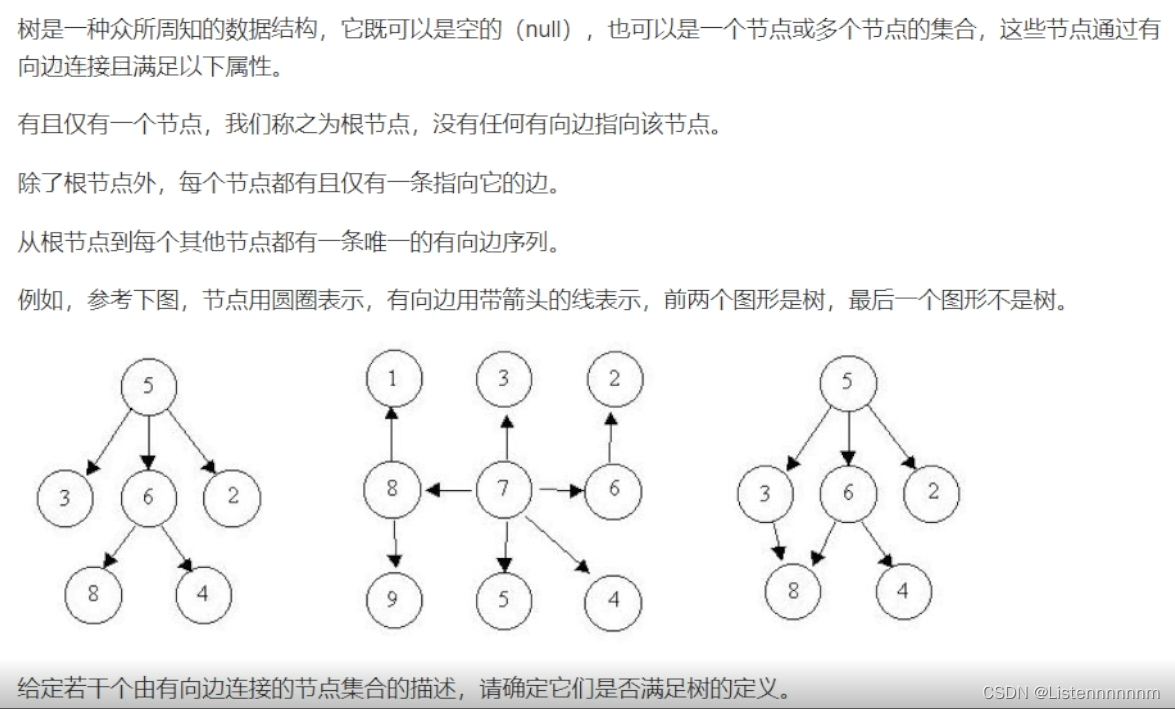
题干

C++实现

树结构需要满足的三个条件

• 不存在入度大于2的结点
• 已连通的u，v，再加入一条新边就会成环
• 边数 = 顶点数-1

#include <iostream>
#include <vector>
using namespace std;

//并查集的应用：判断图的连通性

int set[10001];
//i下标是集合数据编号,set[i]是i的父亲的编号
//若i是根，可令set[i] = i
void InitDisjointSet(int n) {
    for(int i = 0; i<n; ++i) {
        set[i] = i;
    }
}

int FindDisjointSet(int u) {
    if(u == set[u]) {
        return u;
    } else {
        set[u] = FindDisjointSet(set[u]);//压缩路径
        return set[u];
    }
}

int UnionDisjointSet(int u,int v) {
    int uRoot = FindDisjointSet(u);
    int vRoot = FindDisjointSet(v);
    //把v并到u上
    set[vRoot] = uRoot;
}

int main() {
    int u,v;
    InitDisjointSet(10001);
    int edgeCount = 0;
    int vertexCount = 0;
    //vertex[i] = 0说明i未出现过
    vector<int> vertex(10001);
    //inDegree[i]记录i的入度
    vector<int> inDegree(10001);
    //判断是否是棵树
    bool isOK = true;
    int caseIndex = 1;
    while(1) {
        scanf("%d%d",&u,&v);
        if(u == -1&&v==-1) {
            break;
        } else if(u == 0 && v==0) {
            //一个图的所有边已经记录完成了
            if(vertexCount!=edgeCount+1) {
                isOK =false;//有特例：空树
            }
            if(vertexCount == 0 &&edgeCount ==0) {
                isOK = true;
            }

            if(isOK) {
                printf("Case %d is a tree.\n",caseIndex);
            } else {
                printf("Case %d is not a tree.\n",caseIndex);
            }

            InitDisjointSet(10001);
            edgeCount = 0;
            vertexCount = 0;
            for(int i = 0; i<10001; ++i) {
                vertex[i] = 0;
                inDegree[i] = 0;
            }
            isOK = true;
            ++caseIndex;
        } else {
            //往当前图加入新边
            ++edgeCount;
            if(vertex[u] == 0) {
                vertex[u] = 1;
                ++vertexCount;
            }
            if(vertex[v] == 0) {
                vertex[v] = 1;
                ++vertexCount;
            }
            if(FindDisjointSet(u) == FindDisjointSet(v)) {
                //说明成环了
                isOK = false;
            } else {
                UnionDisjointSet(u,v);
            }
        }
        ++inDegree[v];
        if(inDegree[v]>=2) {
            isOK = false;
        }
    }
}