线性表中存放的是同一类型的元素，而广义表是线性表的推广，即广义表中除包含类型相同的元素外，还可以包含具有其自身结构的元素。在人工智能领域使用十分广泛的 LISP语言中，广义表是一种基本数据类型，LISP 语言中的数据和函数都是采用符号表达式定义的，这种符号表达式就是广义表。

广义表的定义及表示

        广义表(Generalized Table）是n（n>=0）个元素的有限序列，表示为 gt =（a1，a2，...，an），其中每一个元素 ai 或者是原子，或者是一个广义表，n 为 gt 的长度，称为表长，原子为广义表中不可再分的数据元素，gt 中的广义表称为 gt 的子表。
        广义表的书面表示方法是将所有元素包含在一对圆括号中，元素之间用逗号分隔，并规定用大写英文字母表示广义表，用小写英文字母表示原子。若广义表为空(n=0)，则表示广义表中没有任何元素，表示为 “()” ；若广义表 gt 非空，则称第一个元素 a1 为 gt 的表头，其余元素组成的表(a2，a3，...，an) 称为  gt 的表尾。显然，表头可能是原子，也可能是一个广义表，但表尾一定是广义表。
        子表中的元素也可以是广义表，这样使得广义表一般呈现层次结构（递归广义表除外)，类似于树形结构，子表嵌套的最大层次称为广义表的深度，广义表的深度也可以看成广义表的括号表示中括号嵌套的最大次数。

【例】各种类型的广义表的表长、表头、表尾与表的深度

A =（)：空表，表长为0，表头为空(原子)，表尾为空表，深度为0。
B=(a，b，c)：表长为3，表头为原子a，表尾为(b，c)，其三个元素都为原子，退化为线性表，表的深度为 1。
C=((a,b)，c，(d，e，t)）：表长为3，表头为广义表(a，b），表尾为(c，(d，e，t)），表的深度为2。
D=(a，D）：具有递归特性的广义表，称为递归广义表，即广义表以自己作为子表，相当于D=(a，(a，(a，……)），表的深度为无穷大。如果在广义表的子表中以当前广义表作为自己的子表，如D=(a，（b，D)），这类广义表也是递归广义表，与间接递归对应，可以称为间接递归广义表。如果广义表的子表是递归的，则该广义表也是递归的。

（为了区分，图中的有向单线表示指向下一个结点的指针（next），有向双线表示指向子表的指针（link））

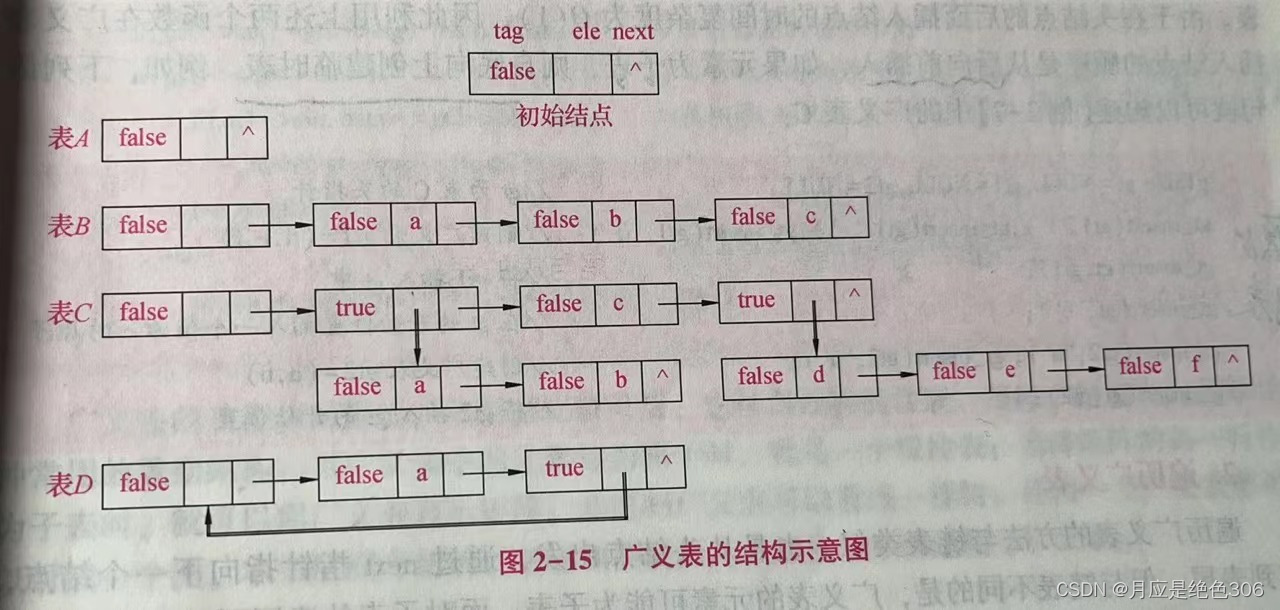
          通常用带头结点的链表表示广义表。由于链表中的结点可能为原子，也可能为子表，因此在结点中需要加一个标志 tag标明该结点的类型，并规定：
         (1)当tag 为false 时，结点为原子；
         (2)当tag 为true时，结点为子表。

#include<iostream>
using namespace std;
typedef char datatype;

typedef struct gtNode {
	bool tag; //tag为false，表示原子，tag为true，表示子表
	/*
		为了有效的利用存储空间，在广义表的类型定义中用一个共用体ele存放结点的元素，
		当tag=false时，ele存放的是原子的值（data）；
		当tag=true 时，ele存放的子表的头结点（link）。
		即data和link二选一。
	*/
	union {
		datatype data;
		gtNode* link;
	}ele;
	gtNode* next;
	gtNode() :tag(false),next(NULL){
		ele.data = '\0';
		ele.link = NULL;
	};
}*gTable;

//广义表中插入结点操作
// 利用以下两个函数在广义表插入结点的顺序是从后往前插入
// 如果元素为子表，则自底向上创建临时表
//在结点gt的后面插入一个原子，原子的值为x
void gt_insert(gTable& gt, datatype x) {
	if (gt == NULL) {
		gt = new gtNode;
	}
	gTable tmp = new gtNode;
	tmp->ele.data = x;
	tmp->next = gt->next; //tmp->tag默认为false
	gt->next = tmp;
}

//在结点gt的后面插入一个子表gt1
void gt_insert(gTable& gt, gTable gt1) {
	if (gt == NULL) gt = new gtNode;
	gTable tmp = new gtNode; //定义子表的头结点
	tmp->tag = true, tmp->ele.link = gt1;
	tmp->next = gt->next; //将tmp插入gt的后面
	gt->next = tmp;
}

//遍历广义表(但不适合递归广义表，会出现死循环）
void gt_traverse(gTable gt) {
	gt = gt->next;
	while (gt != NULL) {
		if (!gt->tag)cout << gt->ele.data << " ";//输出原子
		else {
			cout << endl << "子表：";
			gt_traverse(gt->ele.link);
			cout << endl;
		}
		gt = gt->next;
	}
}

//判断两个广义表是否相等
//判断两个子表是否相同
bool gt_equal(gTable gt1, gTable gt2) {
	gt1 = gt1->next, gt2 = gt2->next;
	if (gt1 == NULL && gt2 == NULL)return true; 
	if (gt1 == NULL || gt2 == NULL)return false;

	if (gt1->tag != gt2->tag) return false;

	if (gt1->tag == false) {
		if (gt1->ele.data == gt2->ele.data)
			return gt_equal(gt1, gt2);
		else
			return false;
	}
	else //当前结点都为子表，则比较子表
		return gt_equal(gt1->ele.link, gt2->ele.link);
}

int main()
{
	gTable gt = NULL, gt1 = NULL, gt2 = NULL; //gt为表的头指针
	gt_insert(gt1, 'f'), gt_insert(gt1, 'e'), gt_insert(gt1, 'd'); //创建广义表gt1=（d,e,f);
	gt_insert(gt, gt1); //将gt1插入gt中
	gt_insert(gt, 'c'); //在gt的开始位置插入一个值为c的原子
	gt_insert(gt2, 'b'); 
	gt_insert(gt2, 'a');//创建广义表gt2=（a，b）
	gt_insert(gt, gt2); //将gt2插入gt的开始位置

	gt_traverse(gt);
	gt_traverse(gt1);
	gt_traverse(gt2);
}

        广义表的功能相当强大，使用也比较灵活，它可以兼容线性表、矩阵、树和有向图等各种常用的数据结构：当广义表中的元素都为原子时，就是一个线性表；当将矩阵的每一行作为子表时，就可以用广义表表示矩阵；非递归广义表可以看成一棵树；任何一个广义表都可以看成一个图。后面介绍的针对树和图的操作及算法基本都适用于广义表。