2312. 卖木头块

题目描述：

给你两个整数 m 和 n ，分别表示一块矩形木块的高和宽。同时给你一个二维整数数组 prices ，其中 prices[i] = [hi, wi, pricei] 表示你可以以 pricei 元的价格卖一块高为 hi 宽为 wi 的矩形木块。

每一次操作中，你必须按下述方式之一执行切割操作，以得到两块更小的矩形木块：

• 沿垂直方向按高度 完全 切割木块，或
• 沿水平方向按宽度 完全 切割木块

在将一块木块切成若干小木块后，你可以根据 prices 卖木块。你可以卖多块同样尺寸的木块。你不需要将所有小木块都卖出去。你 不能 旋转切好后木块的高和宽。

请你返回切割一块大小为 m x n 的木块后，能得到的 最多 钱数。

注意你可以切割木块任意次。

示例 1：

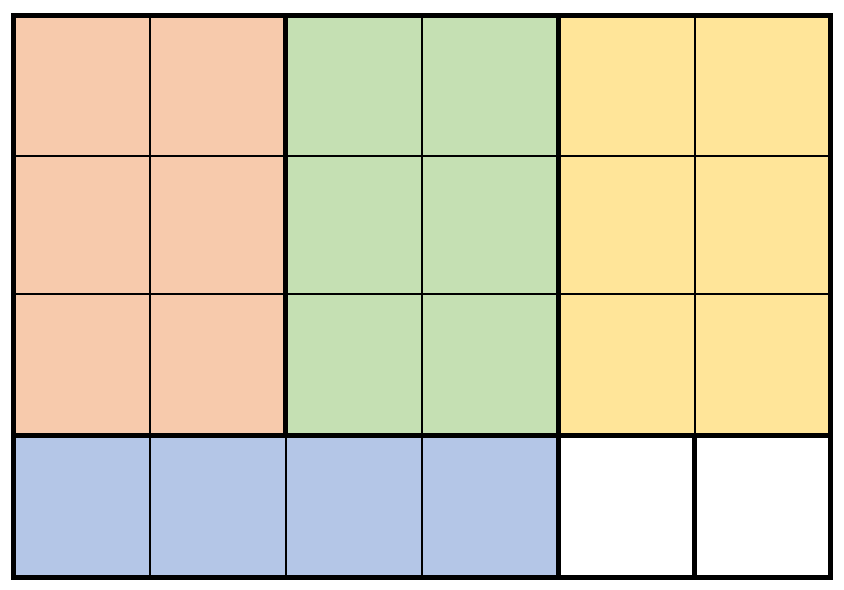
输入：m = 3, n = 5, prices = [[1,4,2],[2,2,7],[2,1,3]]
输出：19
解释：上图展示了一个可行的方案。包括：
- 2 块 2 x 2 的小木块，售出 2 * 7 = 14 元。
- 1 块 2 x 1 的小木块，售出 1 * 3 = 3 元。
- 1 块 1 x 4 的小木块，售出 1 * 2 = 2 元。
总共售出 14 + 3 + 2 = 19 元。
19 元是最多能得到的钱数。

示例 2：

输入：m = 4, n = 6, prices = [[3,2,10],[1,4,2],[4,1,3]]
输出：32
解释：上图展示了一个可行的方案。包括：
- 3 块 3 x 2 的小木块，售出 3 * 10 = 30 元。
- 1 块 1 x 4 的小木块，售出 1 * 2 = 2 元。
总共售出 30 + 2 = 32 元。
32 元是最多能得到的钱数。
注意我们不能旋转 1 x 4 的木块来得到 4 x 1 的木块。

提示：

• 1 <= m, n <= 200
• 1 <= prices.length <= 2 * 10^4
• prices[i].length == 3
• 1 <= h_i <= m
• 1 <= w_i <= n
• 1 <= pricei <= 106
• 所有 (h_i, w_i) 互不相同 。

思路：

每块板子 m * n ，可以横向切割，可以纵向切割。
横向切割依次计算 1 * n + (m - 1) * n, 2 * n + (m -2) * n, ......
纵向切割依次计算 m * 1 + m * (n - 1), m * 2 + m * (n - 2), ......
以及 prices 里 m * n 的价格，最大值为这块板子的最高价格，缓存之。

反过来，从1 * 1推算，就是dp。

代码：

class Solution {
    public long sellingWood(int m, int n, int[][] prices) {
        long[][] map= new long[m+1][n+1];
        long[][] pr= new long[m+1][n+1];
        //初始化map数组
        for(int i = 0; i < m + 1; i++) {
            for(int j = 0; j < n + 1; j++) {
                map[i][j] = -1;
            }
        }
        //配置价格数组
        for(int[] p : prices){
            pr[p[0]][p[1]] = (long) p[2];
        }
        return dfs(m,n,map,pr);
    }
    private long dfs(int m, int n, long[][]map, long[][] pr){
        if(map[m][n]!=-1)return map[m][n];
        long p=pr[m][n];

        for(int i=1;i<=m/2;i++){
            long t = dfs(i,n,map,pr)+dfs(m-i,n,map,pr);
            p=Math.max(p,t);
        }
        for(int i = 1; i <= n / 2; i++) {
            long t = dfs(m, i, map, pr) + dfs(m, n - i, map, pr);
            p = Math.max(t, p);
        }  
        map[m][n]=p;
        return p;
    }
}