目录
0 目标
1 构造模型
1.1 构造模型的思路
1.2 具体模型构造的EXCEL公式和过程
2 直接用EXCEL画图，然后生成趋势线的方式进行回归分析
2.1 先选择“观测值Y”的数据，用散点图或者折线图作图
2.2 然后添加趋势线和设置趋势线格式
2.3 生成趋势线
3 使用EXCEL的 数据/数据分析/回归功能
3.1 功能入口：数据/数据分析/回归功能
3.2 进行回归时，需要注意2个点
3.3 回归分析的结果
4 逐个手动重算“回归统计”里的几个指标
4.1 相关系数
4.1.1 公式
4.1.2 以下是详细计算过程
4.2 先求 SSE SSR SST 以及OLS，再求R2
4.3 决定系数R**2
4.3.1 公式
4.3.2 R2具体计算
4.4 调整后的R2
4.5 标准误差 SEE
4.6 观测值
5 逐个手动重算“方差分析”里的几个指标
5.1 自由度 DF
5.2 关于SS离差的3个类型 SSR, SSE ,SST
5.3 均方MS
5.3.1 定义
5.3.2 公式
6 RESIDUAL OUTPUT
6.1 残差= y=y^= 观测值-预测值
7 多个模拟直线比较
8 未完成的部分 F检验的显著度 和 T检验的P值 （需要学习F检验，T检验的知识！）
9 未解决的问题
10 python 模拟实操，缺！
0 目标
- 目标：用EXCEL做一元线性回归的各种参数，手动计算验证EXCEL计算的各个参数的值，自己重新算一遍，了解具体的公式计算过程。
- 为什么要这么做
- 看了这么多讲指标运算公式的，大多数都是推导。但很少见到有自己手动，完全验证一遍这些指标计算公式实操的，我自己试试。
- 目的2个：
- 还能验证自己整理的公式的对错。
- 可以加深对公式的理解
1 构造模型
1.1 构造模型的思路
- 正常思路：(先有我们大脑里的理想值,也就是假设)→先有观测值 →再回归模型→预测值
- 我的构造思路: 先作假一个理想数据(公式生成)→生造观测值(加rand扰动)→再回归模型→预测值
- 为什么要这么搞？
- 这样我自己相当于，先掌握了理想数据=“正确答案”，然后可以比较到底什么样的模拟更接近我这个预设的正确答案。
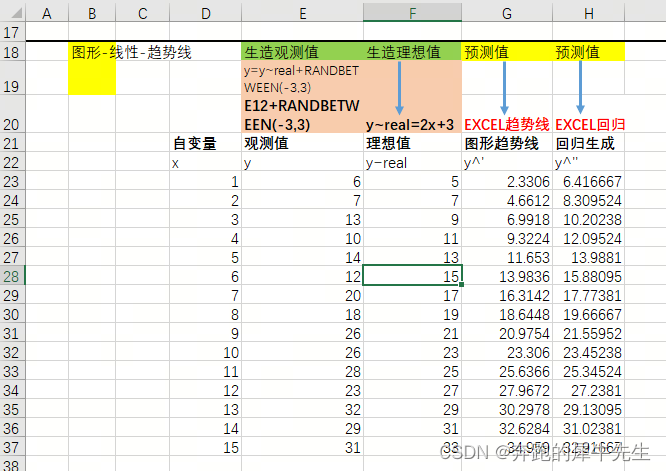
1.2 具体模型构造的EXCEL公式和过程
- 理想数据
- X：1，2 ...15
- Y： Y=2x+3
- 观测值
- y=y~real+RANDBETWEEN(-3,3)
2 直接用EXCEL画图，然后生成趋势线的方式进行回归分析
见下图
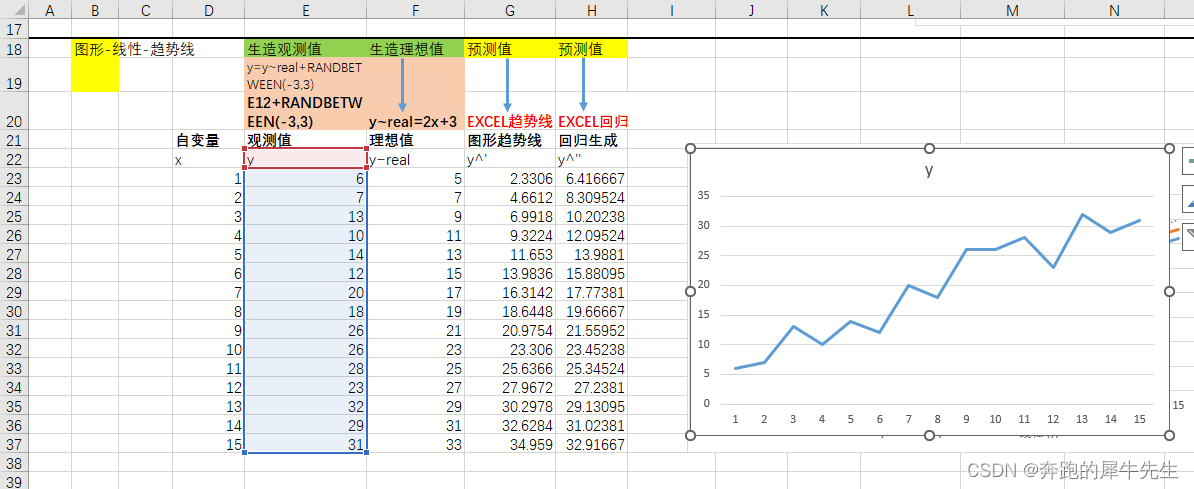
2.1 先选择“观测值Y”的数据，用散点图或者折线图作图
作图格式
- 可以选择连线的散点图，或者折线图
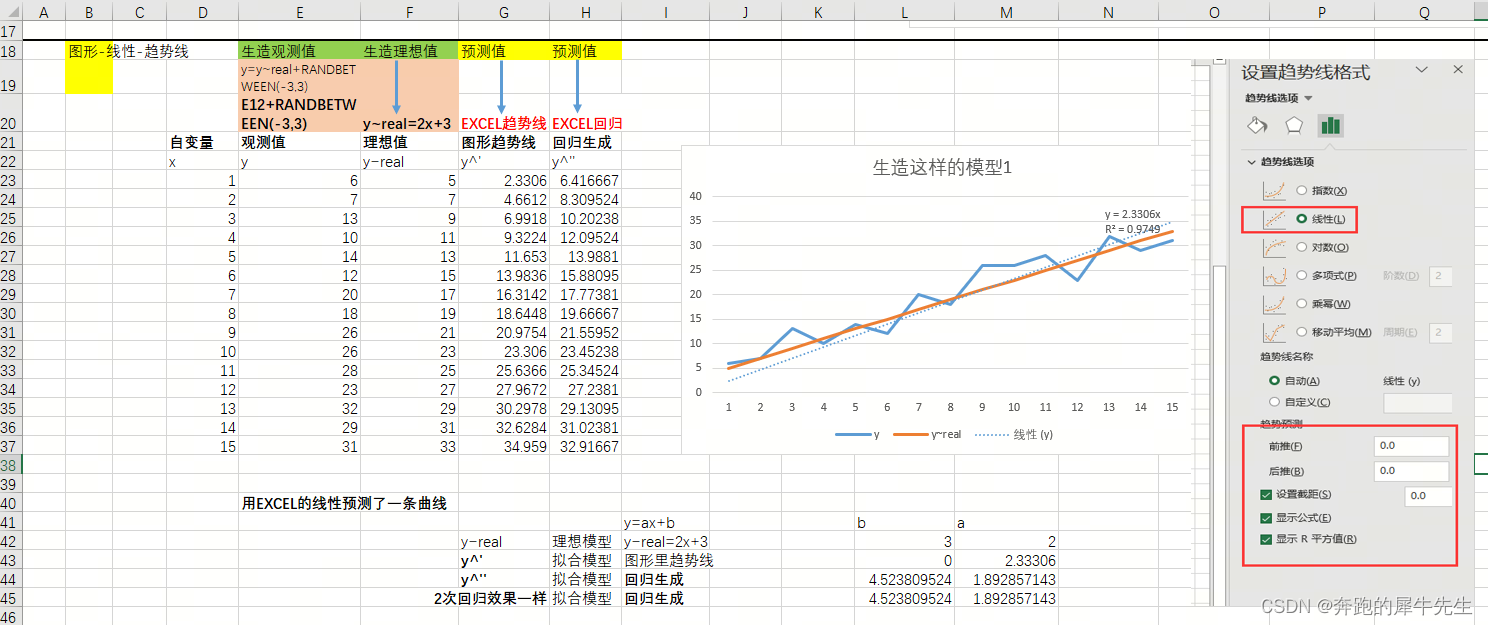
2.2 然后添加趋势线和设置趋势线格式
- 因为做的是一元线性回归，这里记得选择直线
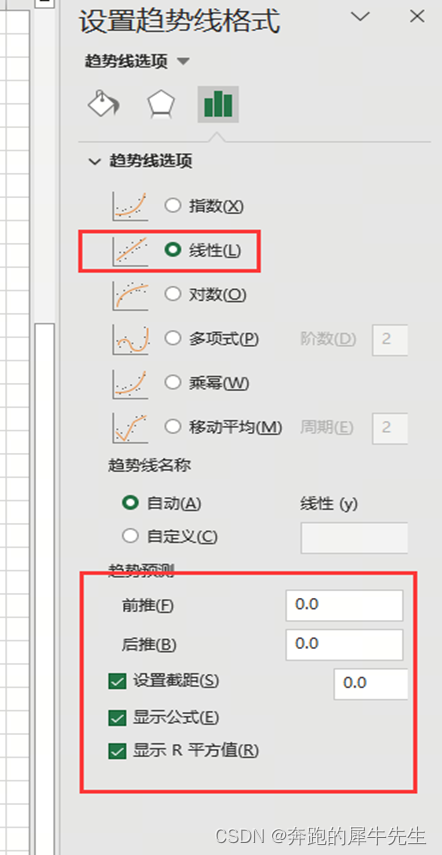
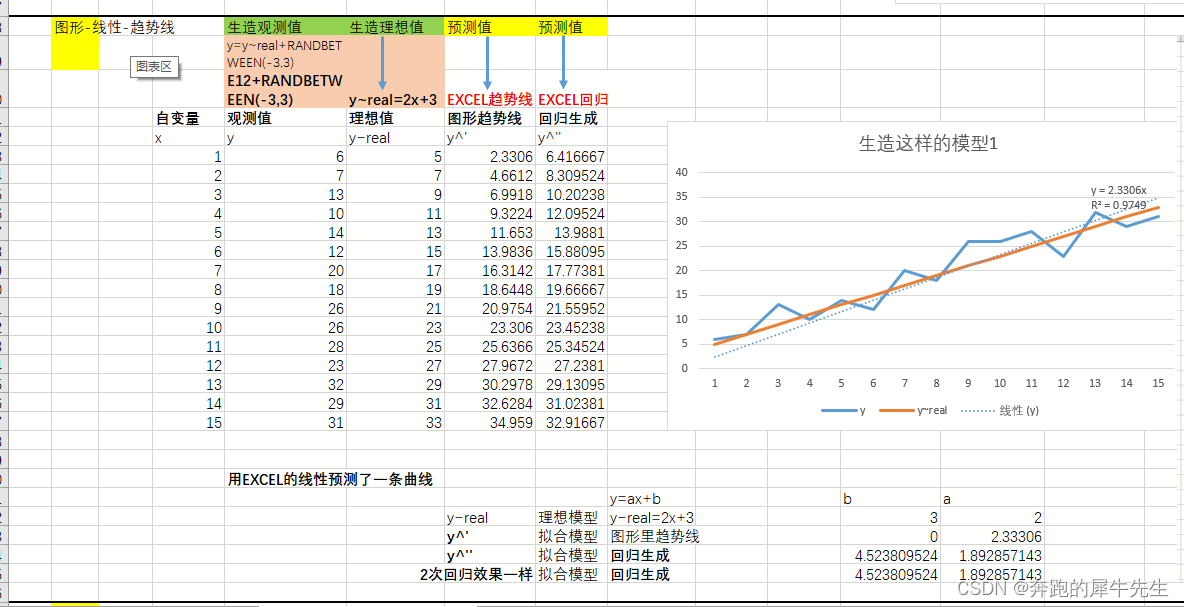
2.3 生成趋势线
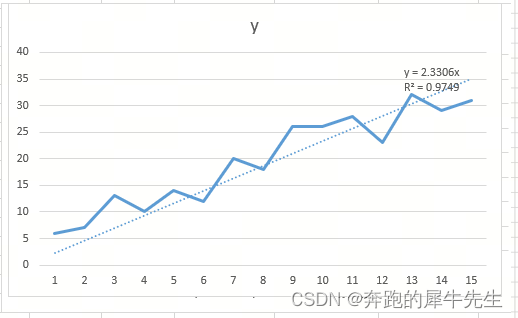
生成一个一元函数的趋势线： 直线
- 其中 y=ax+b，具体为y=2.33306x
- a=2.33306
- b=0
- R**2=0.9749
3 使用EXCEL的 数据/数据分析/回归功能
- 基本内容如下
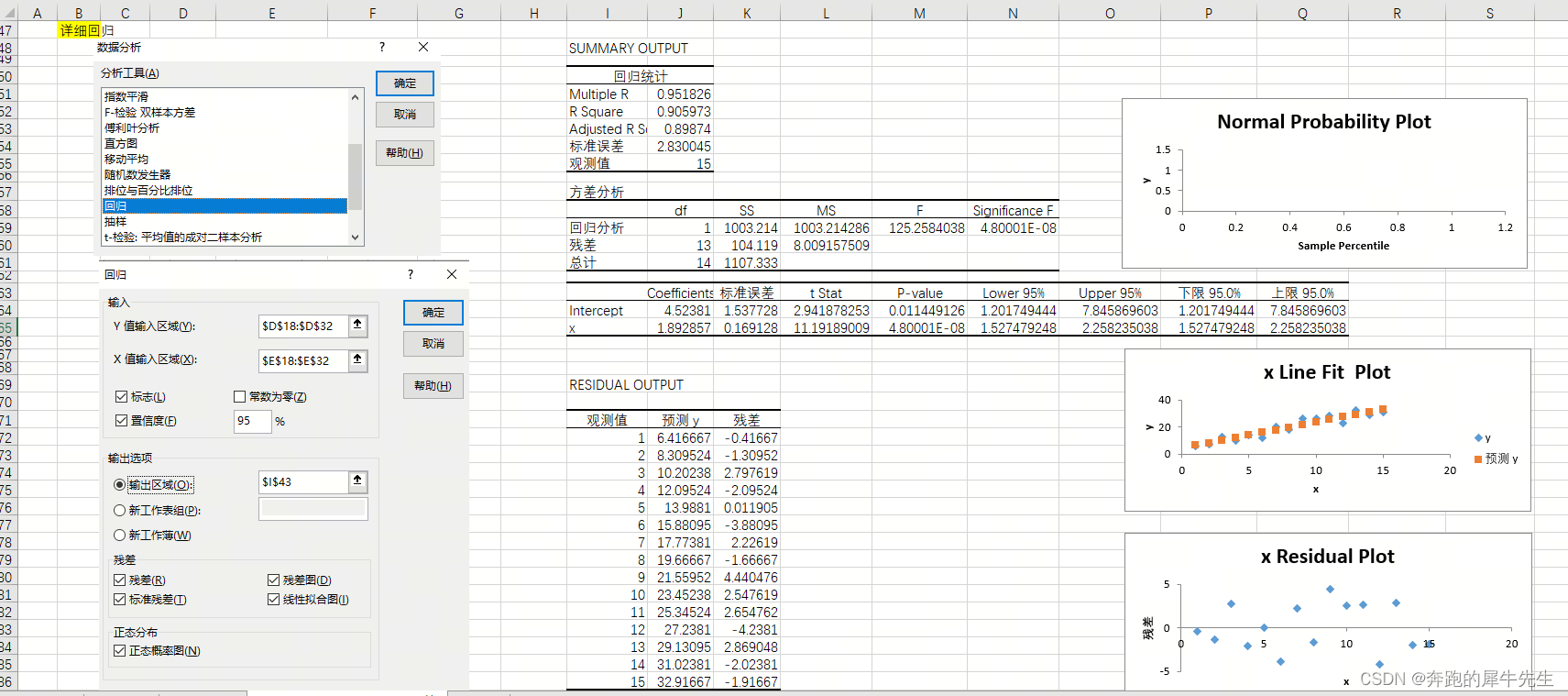
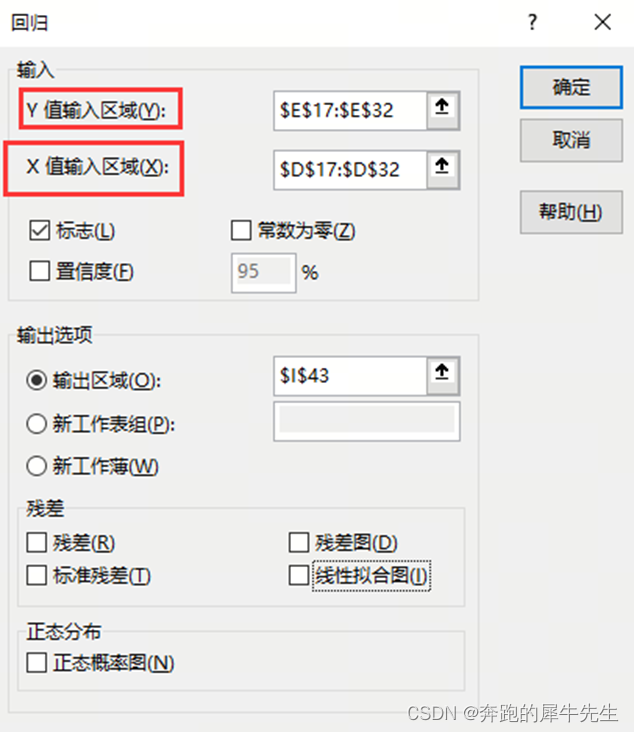
3.1 功能入口：数据/数据分析/回归功能
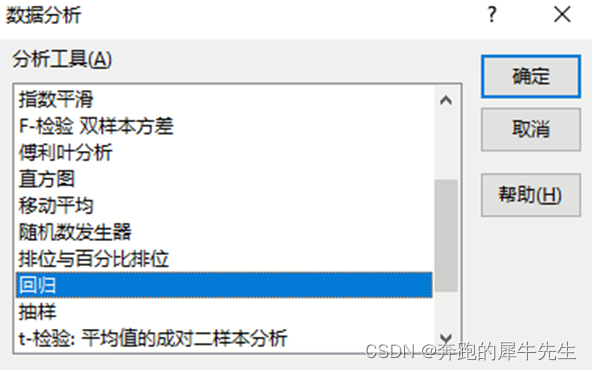
3.2 进行回归时，需要注意2个点
- 1 注意回归面板上，Y值在上面，X值在下面。容易选错
- 2 下面哪些勾选项，做简单回归分析可以不勾
- 3 详细的回归可以都勾选
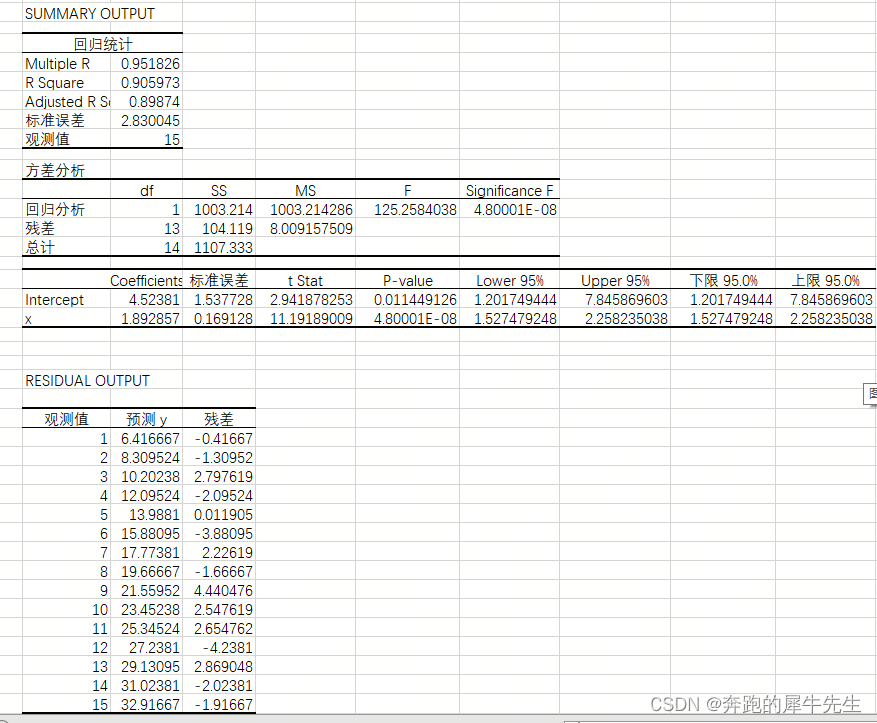
3.3 回归分析的结果
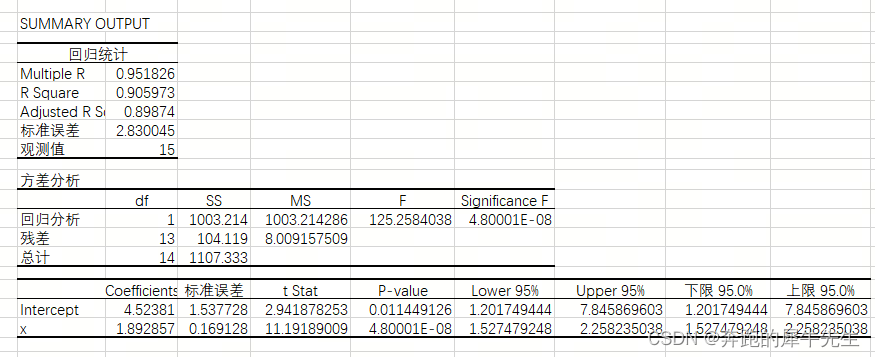
4 逐个手动重算“回归统计”里的几个指标
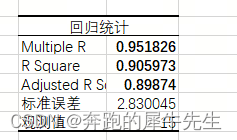
4.1 相关系数
4.1.1 公式
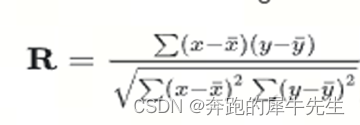
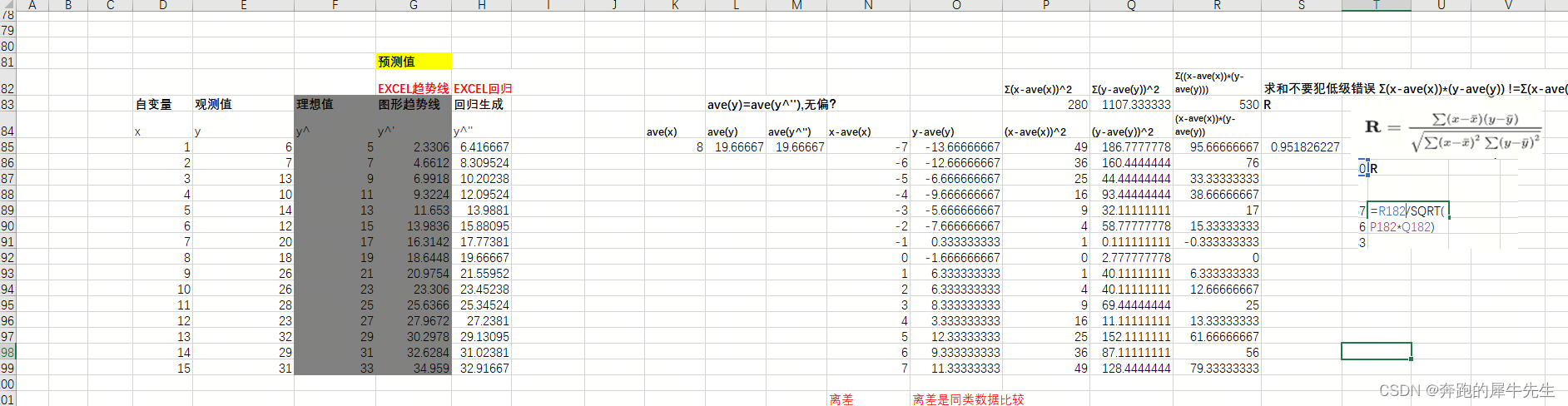
4.1.2 以下是详细计算过程
- 手动计算的和回归分析的R相等
- 求和不要犯低级错误 Σ(x-ave(x))*(y-ave(y)) !=Σ(x-ave(x))*Σ(y-ave(y))
- R=Σ((x-ave(x))*(y-ave(y))) /SQRT(Σ(x-ave(x))^2*Σ(y-ave(y))^2)
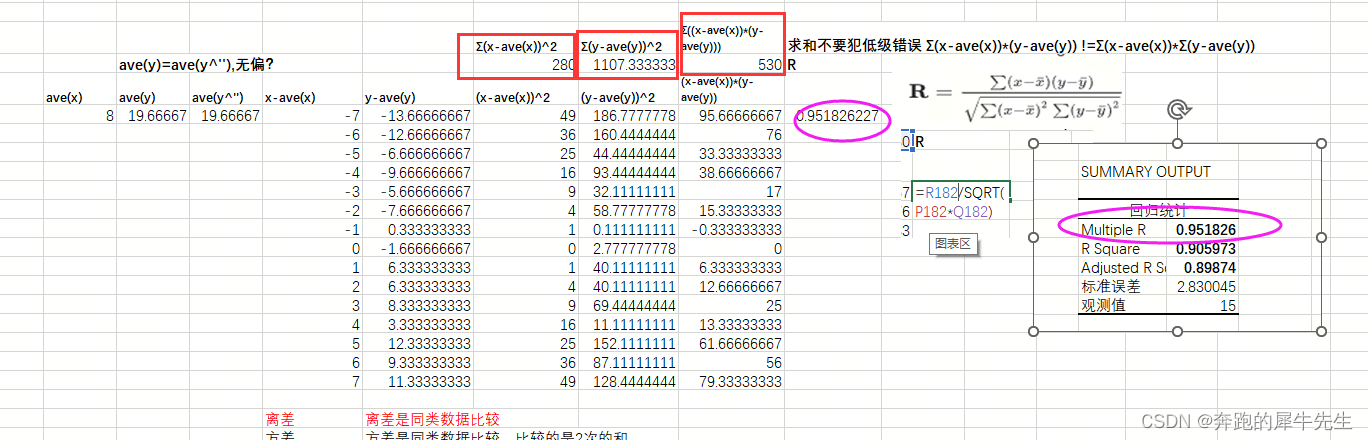
4.2 先求 SSE SSR SST 以及OLS，再求R2
- SSE: 残差平方和， Σ(y-y^'')^2
- SSR：回归平方和 ，Σ(y^''-ave(y))^2
- SST：离差平方和，总体平方和， Σ(y-ave(y))^2
- OLS最小二乘法的=SS=SSE=残差平方和
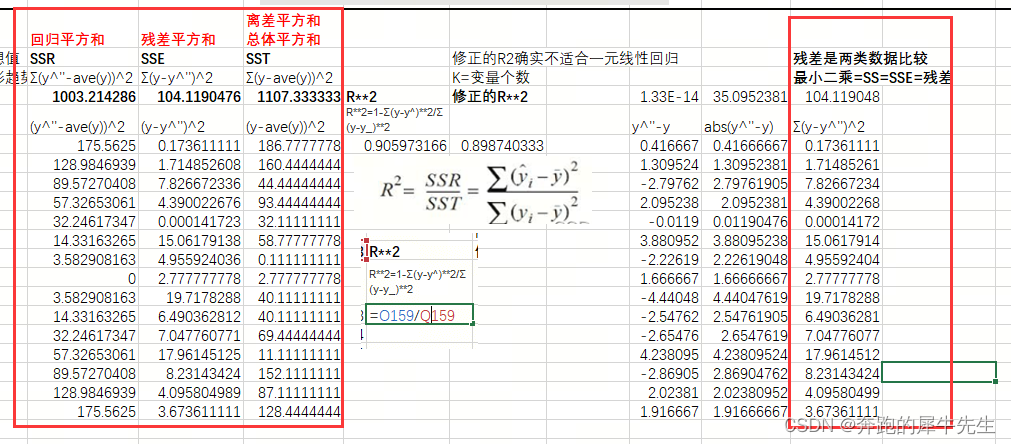
4.3 决定系数R**2
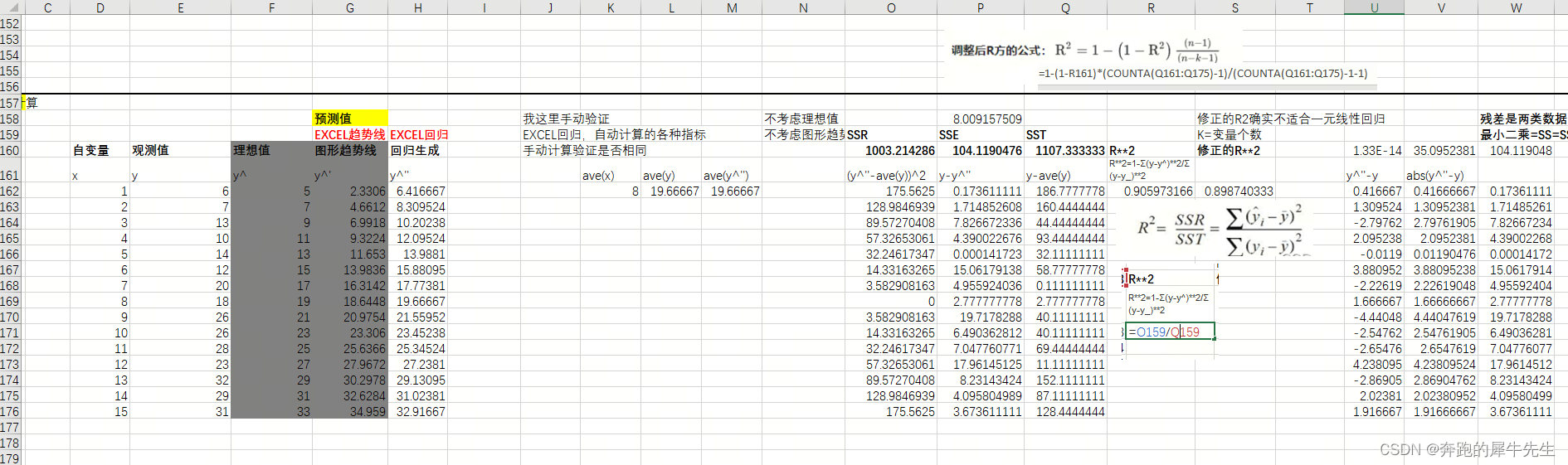
4.3.1 公式
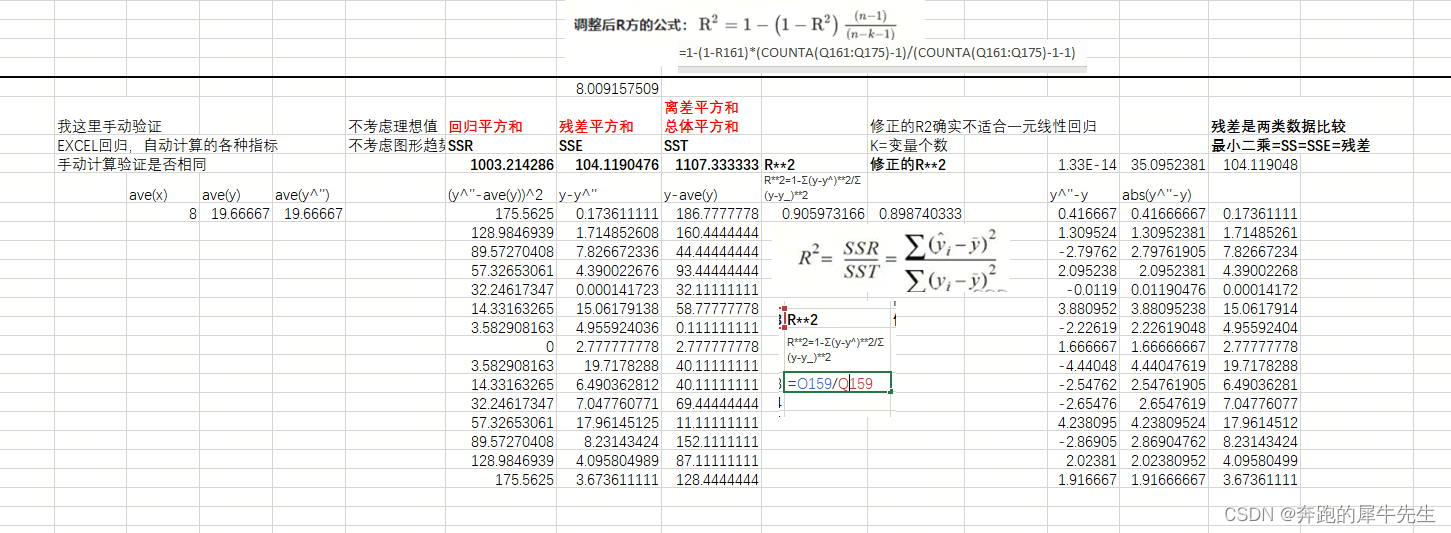
4.3.2 R2具体计算
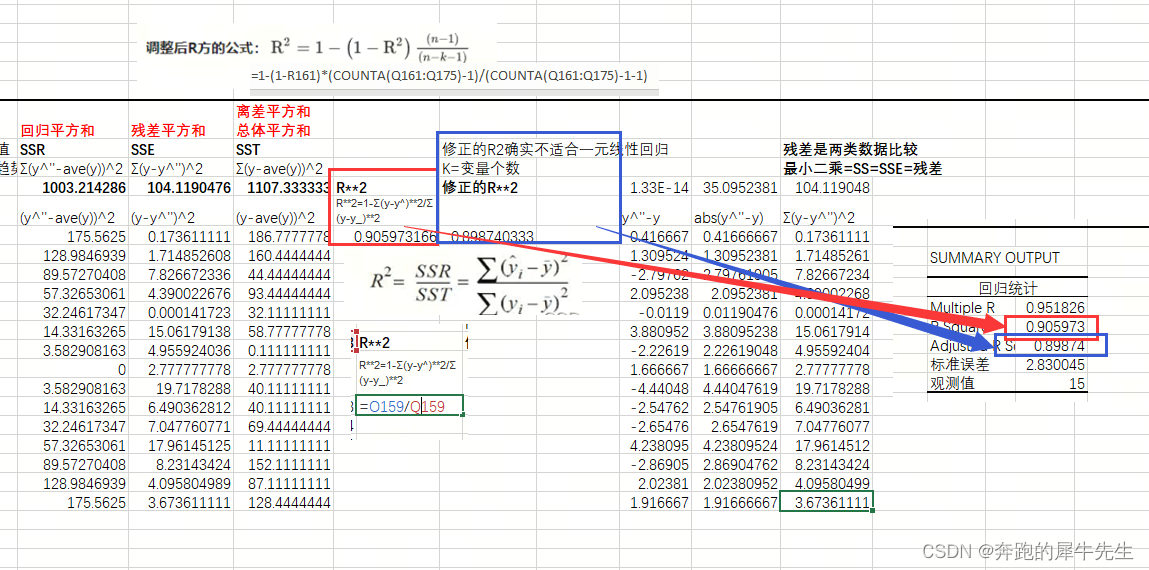
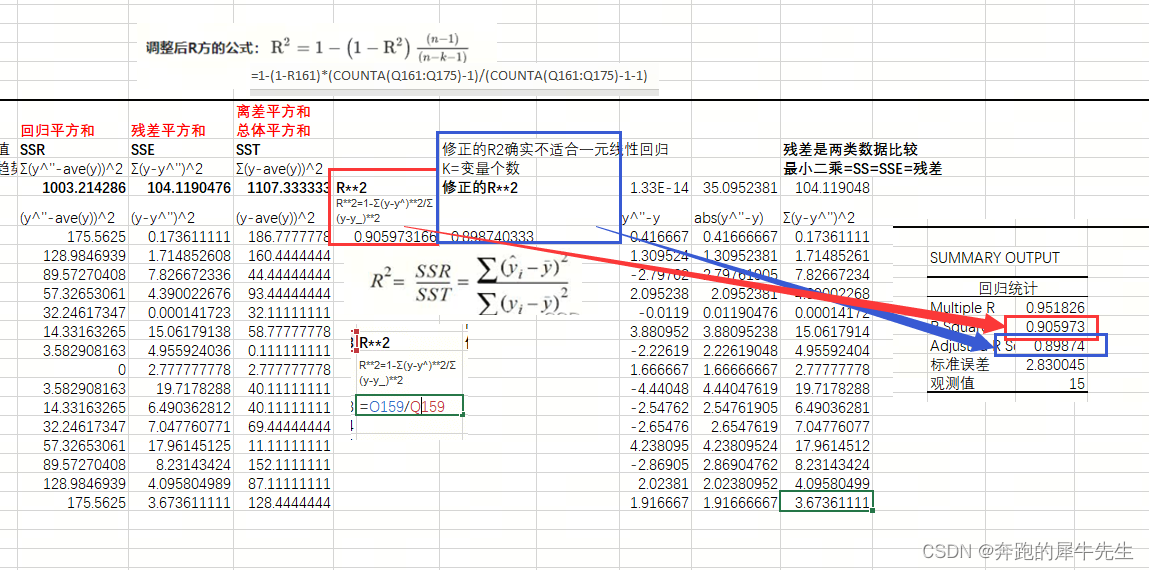
4.4 调整后的R2
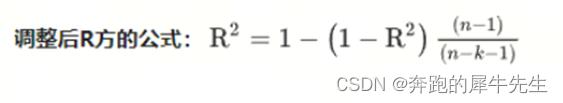
- 修正的R2确实不适合一元线性回归
- K=变量个数
- 只有1个变量是，修正的R2会变小
- 修正的R2看起来确实只适合多元线性回归
4.5 标准误差 SEE
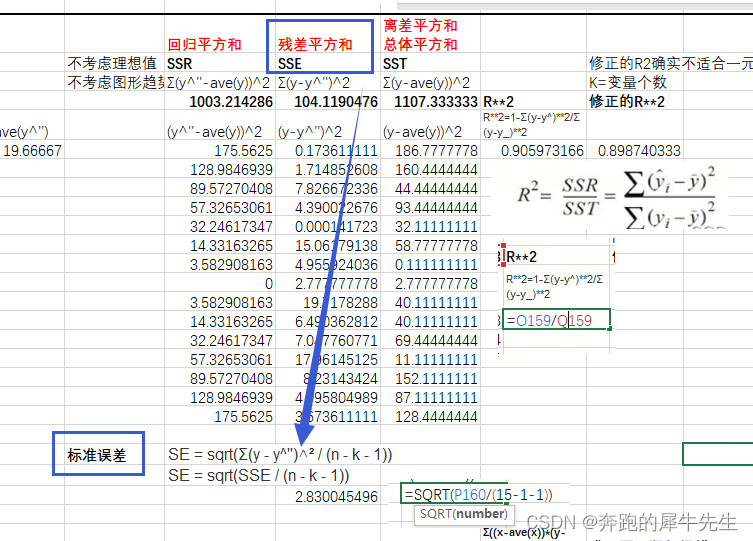
- 标准误差SEE
- SEE = sqrt(Σ(y - y^'')^² / (n - k - 1))
- SEE = sqrt(SSE / (n - k - 1))
- 并不是 /n
4.6 观测值
观测值=样本数量=15，没什么好说的。
5 逐个手动重算“方差分析”里的几个指标
- df：degree of freedom 自由度
- ss：离均差平方和
- ms ：均方
5.1 自由度 DF
详细内容看上次的关于自由度的文章
【小白学机器学习8】统计里的自由度DF=degree of freedom, 以及关于df=n-k， df=n-k-1, df=n-1 等自由度公式-CSDN博客文章浏览阅读698次，点赞13次，收藏12次。自由度通常用于抽样分布中。统计学中：在统计模型中，自由度指样本中可以自由变动的独立不相关的变量的个数，当有约束条件时，自由度减少。样本中独立或能自由变化的数据的个数，称为该统计量的自由度。自由度(degree of freedom, df)指的是计算某一统计量时，取值不受限制的变量个数。https://blog.csdn.net/xuemanqianshan/article/details/136643151?spm=1001.2014.3001.5502
- 回归分析的df,y=a+bx，因为只有1个自变量，所以df=1
- 残差SSE的df
- 这里面需要确定a 和b两个参数，其中a是截距，而b 是x的参数。
- 因为自由度=n-k, 而SSE=Σ(y-y^'')^2 = Σ(y-(a+bx))^2 ，所以df=n-k=n-2=15-2=13
- 或者用多元线性回归的公式 df=n-k-1=15-1-1=13
- 总计的df=方程的df+样本的df=1+13=14
5.2 关于SS离差的3个类型 SSR, SSE ,SST
见上面的分析
5.3 均方MS
5.3.1 定义
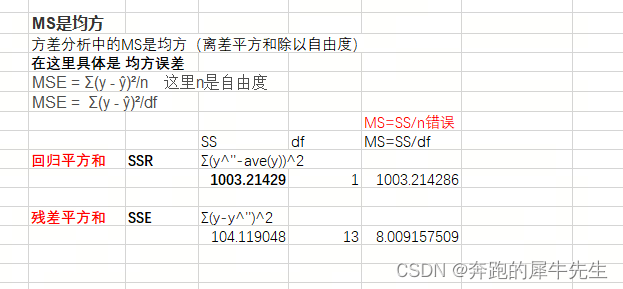
MS是均方
方差分析中的MS是均方（离差平方和除以自由度）
在这里具体是 均方误差
5.3.2 公式
- Mean Square Error 均方误差
- MSE = Σ(y - ŷ)²/n 这里n是自由度
- MSE = Σ(y - ŷ)²/df
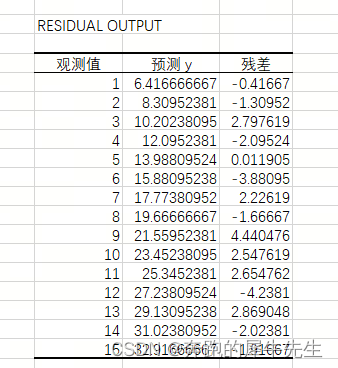
6 RESIDUAL OUTPUT
6.1 残差= y=y^= 观测值-预测值
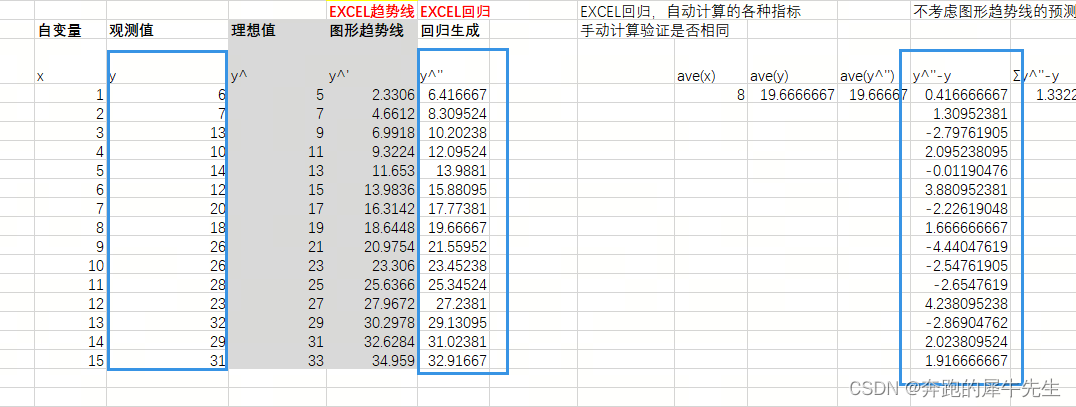
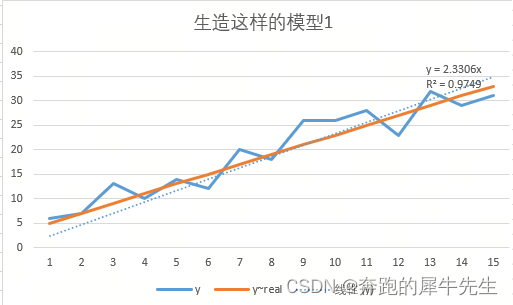
7 多个模拟直线比较
- 暂时看略有差别，差别不大
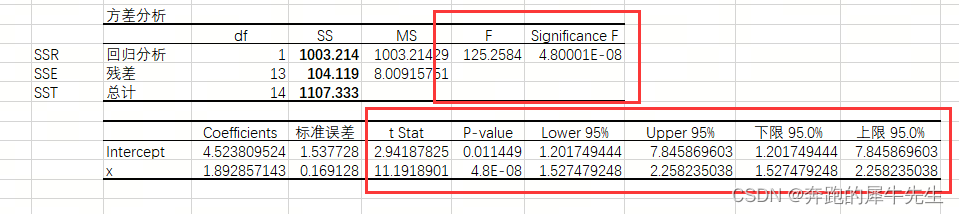
8 未完成的部分 F检验的显著度 和 T检验的P值 （需要学习F检验，T检验的知识！）
- Significance F：越小说明拟合越好
- T检验的P-value：越小说明拟合越好
9 未解决的问题
比如一元线性回归模型中，关于y=ax+b，这里面a 和 b 的标准误差是怎么求出来的？
网上也有人提出了这样的问题，暂时我没看明白，留着
一元回归结果当中，斜率的标准误差是怎么计算出来的？ - 知乎回归系数不是一个确定的值，相反它是一个随机变量，也就是说你不同样本回归得到的回归系数是不一样的，举…
https://www.zhihu.com/question/297956772/answer/1032593129?utm_id=0
一元回归结果当中，斜率的标准误差是怎么计算出来的？ - 知乎深夜吃西瓜碰到回答一下！！首先，记住因为误差项的存在，所以参数的方差才不等于0，只要理解了回归的含…https://www.zhihu.com/question/297956772/answer/1302721483
其他
RM
回归模型（regression model）对统计关系进行定量描述的一种数学模型。如多元线性回归的数学模型可以表示为y=β0+β1*x+εi，式中，β0，β1，…，βp是p+1个待估计的参数，εi是相互独立且服从同一正态分布N(0,σ2)的随机变量，y是随机变量；x可以是随机变量，也可以是非随机变量,βi称为回归系数，表征自变量对因变量影响的程度。
OLS，是 普通最小二乘回归模型
ols 全称ordinary least squares，是回归分析（regression analysis）最根本的一个形式
10 python 模拟实操，缺！
