二项分布理论
二项分布是一种离散概率分布,描述了在n次独立重复的伯努利试验中成功的次数的概率分布。其中,每次试验的结果只有两个可能:成功或失败,且每次试验的成功概率p是相同的。
具体来说,如果随机变量X表示在n次试验中成功的次数,那么X服从参数为n和p的二项分布,记为X~B(n,p)。意味着在n次试验中成功的次数为k的概率可以用二项分布的概率质量函数来表示:
二项分布的期望值和方差分别为:
R语言实现
在以下代码中,使用seq()函数创建了一个名为k的向量,该向量从0.1开始,以0.1的步长递增,直到0.9,这个向量稍后将用于指定二项分布的概率参数。
k <- seq(0.1, 0.9, 0.1)使用par()函数来设置图形参数,使用mfrow=c(3,3)设置一个3x3的图形布局,在一个页面中绘制9个图形,每行3个。mai参数设置了图形的边距,四个数字分别代表图形的下、左、上、右边距。
par(mfrow=c(3, 3), mai = c(0.6, 0.5, 0.2, 0.1))使用for循环,用于遍历k向量中的每一个概率值。在循环内部,barplot()函数被用来绘制二项分布的概率条形图。 使用dbinom(0:5, 5,k[i])计算了在给定的概率k[i]下,一个二项随机变量取值为0到5的概率。图形的x轴标签是’x’,y轴标签是’p’。ylim=c(0,0.6)设置了y轴的范围。图形的主标题通过substitute()函数动态生成,显示当前的概率值。最后,col=“lightblue”设置条形图的颜色为浅蓝色。
for(i in 1:9)
barplot(dbinom(0:5, 5, k[i]), xlab="x", ylab="p", ylim=c(0, 0.6),
main=substitute(B(5, b), list(b=k[i])), col="lightblue")
完整版代码:
# 此段代码来源于教材《统计学-基于R语言》
k <- seq(0.1, 0.9, 0.1)
par(mfrow=c(3, 3), mai = c(0.6, 0.5, 0.2, 0.1))
for(i in 1:9)
barplot(dbinom(0:5, 5, k[i]), xlab="x", ylab="p", ylim=c(0, 0.6),
main=substitute(B(5, b), list(b=k[i])), col="lightblue")
生成图像

实例应用
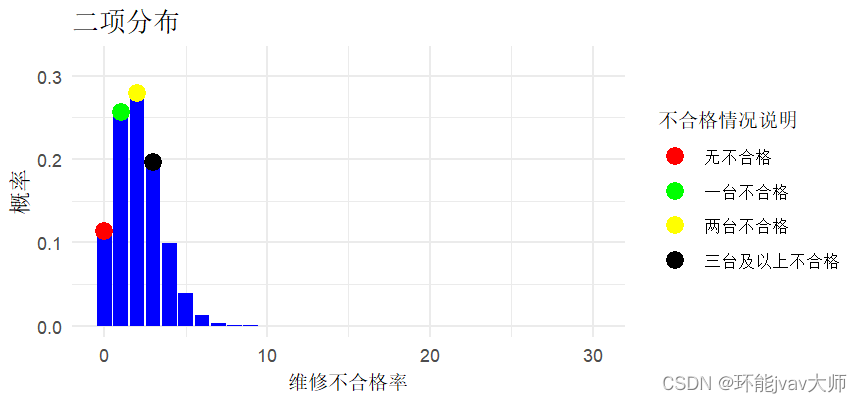
这里用一个我们公司自己的数据,维修车间维修后的设备检测不合格率为7%,从中有放回的抽取30台设备。接下来使用二项分布计算的方式计算出:1.没有不合格品的概率; 2.1台不合格品的概率; 3.三台以上不合格品的概率:
library(ggplot2)
library(dplyr)
n_trials <- 30
prob_failure <- 0.07
df <- tibble(
NumberOfFailures = 0:n_trials,
Probability = dbinom(0:n_trials, size = n_trials, prob = prob_failure)
)
cat("没有不合格品的概率为:", df$Probability[1] * 100, "%\n")
cat("1到3个不合格品的概率为:", sum(df$Probability[2:4]) * 100, "%\n")
MoreThanThree <- 1 - sum(df$Probability[1:4])
cat("3个以上不合格品的概率为:", MoreThanThree * 100, "%\n")
ggplot(df, aes(x = NumberOfFailures, y = Probability)) +
geom_bar(stat = "identity", fill = "blue") +
geom_point(data = df %>% slice(1:4), aes(colour = factor(NumberOfFailures)), size = 4) +
scale_color_manual(values = c("red", "green", "yellow", "black"), name = "不合格情况说明",
labels = c("无不合格", "一台不合格", "两台不合格", "三台及以上不合格")) + theme_minimal() +
labs(x = "维修不合格率", y = "概率", title = "二项分布") +
scale_y_continuous(expand = expansion(mult = c(0.05, 0.2)))输出结果
> 没有不合格品的概率为: 11.33675 %
> 1到3个不合格品的概率为: 73.16518 %
> 3个以上不合格品的概率为: 15.49807 %生成很丑的图形