Welsh, D.J.A. and Powell, M.B. (1967) An Upper Bound for the Chromatic Number of a Graph and Its Application to Timetabling Problems. 《The Computer Journal》, 10, 85-86. 

 《The Computer Journal》

1 图着色算法概述

1967年，Welsh和Powell算法引入了图色数的上界。它提供了一个在静态图上运行的贪婪算法。

顶点根据其度数排序，得到的贪婪着色最多使用颜色，最多比图的最大度数多一个。这种启发式被称为威尔士-鲍威尔算法。

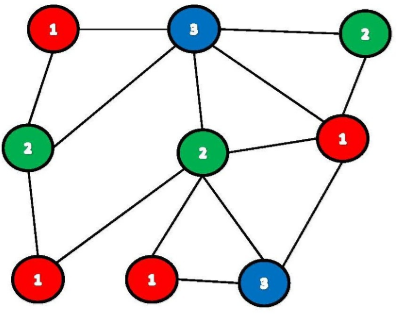
2 伪代码

威尔士鲍威尔算法：

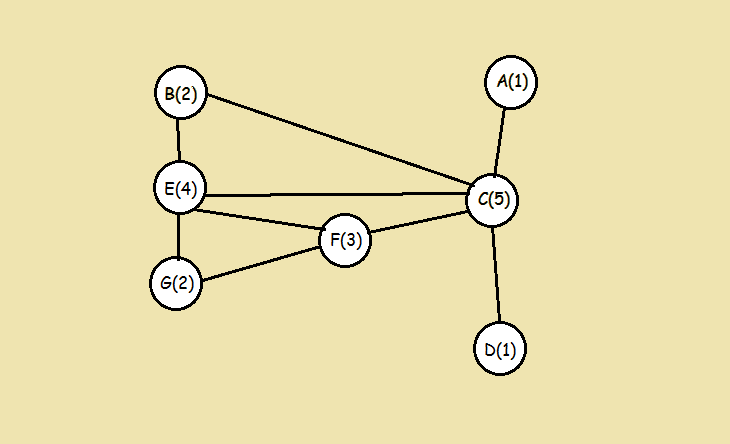
1. 求每个顶点的阶数。
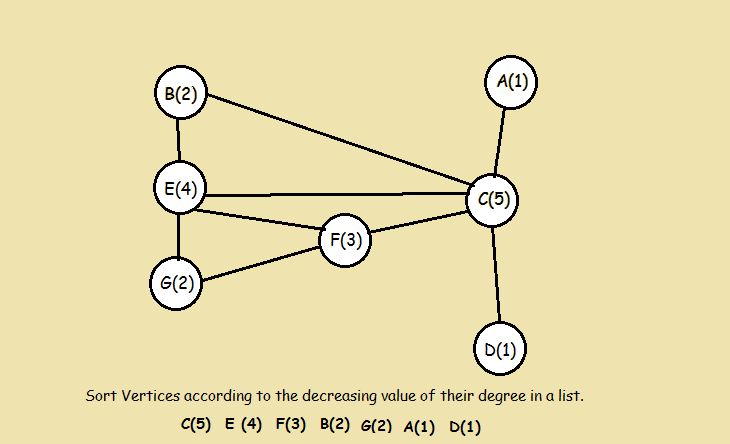
2. 按降价顺序列出顶点，即价度（v（i））>=度（v（i+1））。
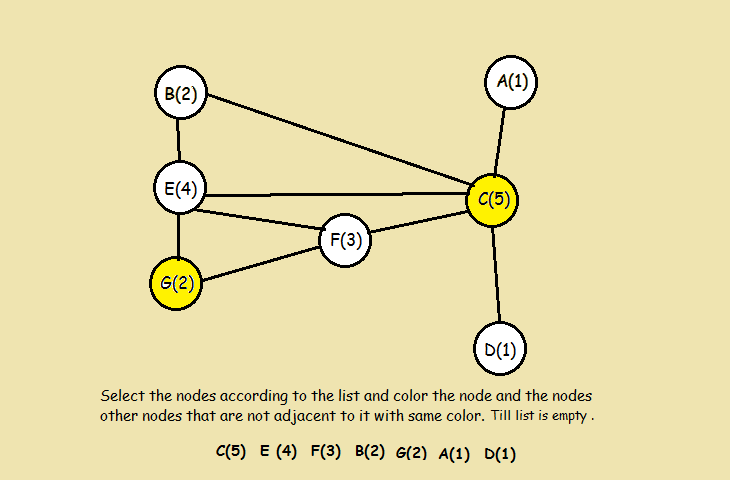
3. 为列表中的第一个顶点上色。
4. 沿着已排序的列表向下，为每个未连接到相同颜色上方的有色顶点着色，然后划掉列表中的所有有色顶点。
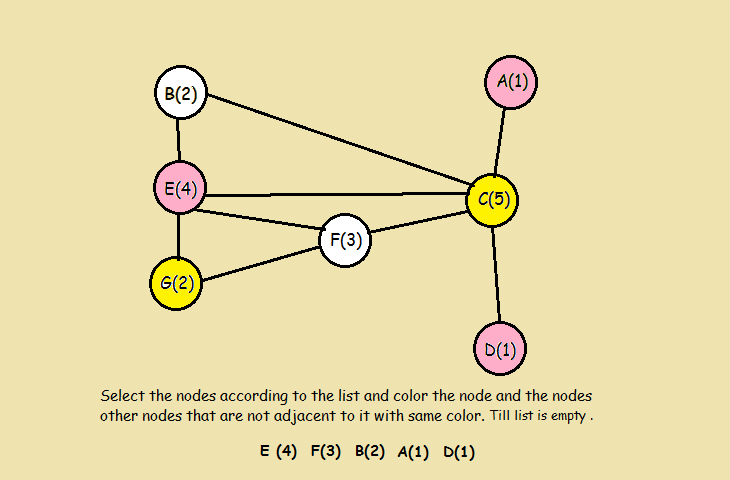
5. 对未着色的顶点重复此过程，使用新颜色始终按度数降序操作，直到所有顶点都按度数降序操作，直到所有顶点都着色为止。

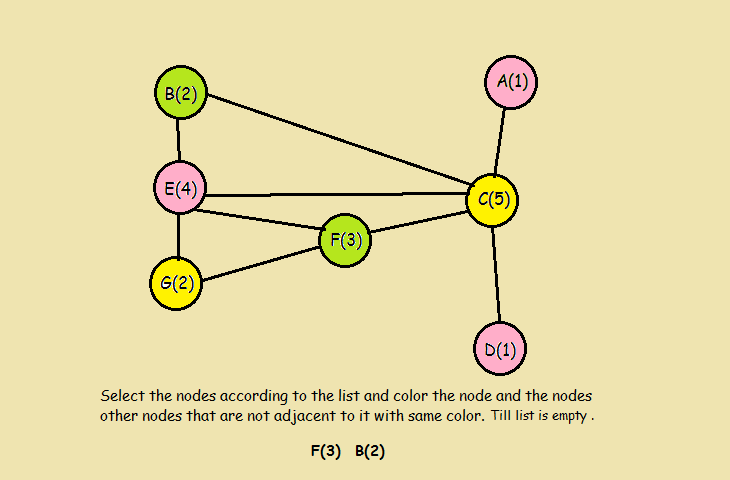
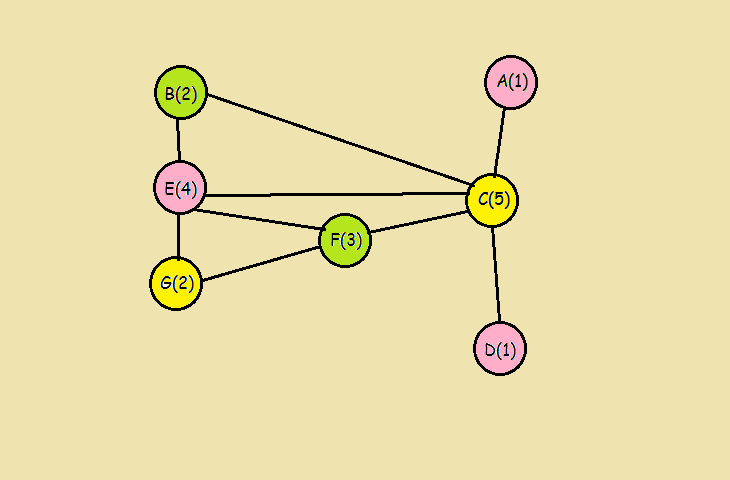
3 源程序

using System;
using System.Collections;
using System.Collections.Generic;

namespace Legalsoft.Truffer.Algorithm
{
    public class Vertex : IComparable<Vertex>
    {
        public int color { get; set; } = 0;
        public int degree { get; set; } = 0;

        public int CompareTo(Vertex o)
        {
            return o.degree - this.degree;
        }
    }

    public class Welch_Powell_Color
    {
        public void Welsh_Powell(int n, Vertex[] vertex, int[,] edges)
        {
            Array.Sort(vertex);

            int ncolor = 0;
            int colored_cnt = 0;
            while (colored_cnt < n)
            {
                ncolor++;
                for (int i = 1; i <= n; i++)
                {
                    if (vertex[i].color == 0)
                    {
                        bool ok = true;
                        for (int j = 1; j <= n; j++)
                        {
                            if (edges[i, j] == 1 && vertex[j].color == ncolor)
                            {
                                ok = false;
                                break;
                            }
                        }
                        if (!ok)
                        {
                            continue;
                        }

                        vertex[i].color = ncolor;
                        colored_cnt++;
                    }
                }
            }
        }
    }
}