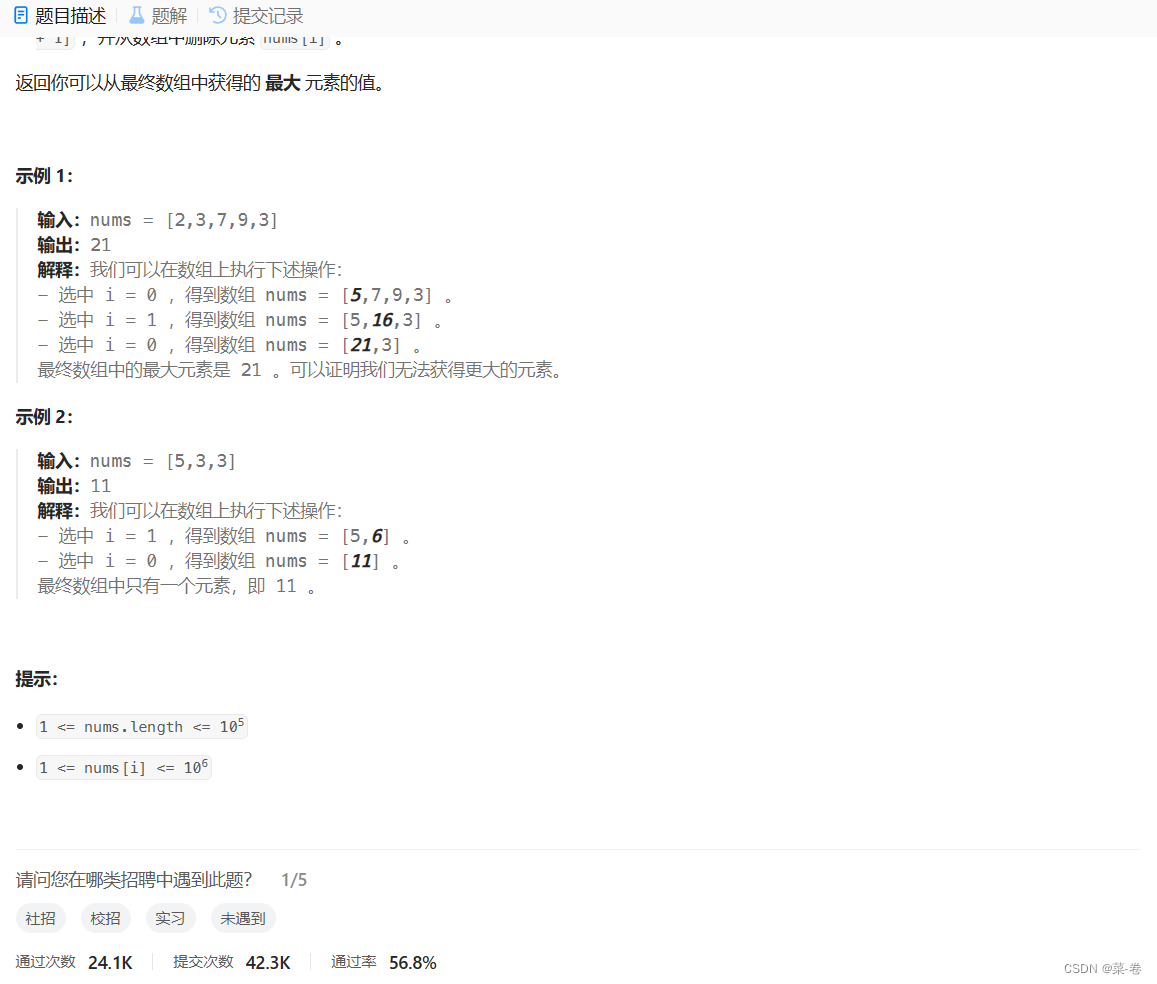
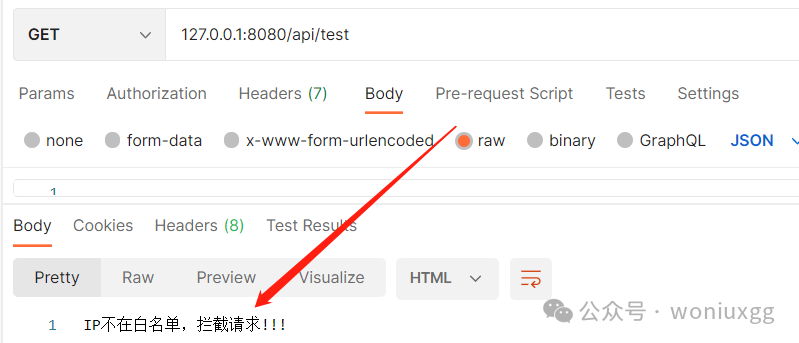
1.重新分装苹果（贪心）

思路

箱子大小降序排序，按顺序装

class Solution {
public:
    int minimumBoxes(vector<int>& apple, vector<int>& capacity) {
        int n = apple.size(), m = capacity.size();
        int sum = 0;
        for(int i = 0; i < n; i++) sum += apple[i];
        sort(capacity.begin(), capacity.end(), greater<int>());
        int cnt = 0, ans = 0;
        for(int i = 0; i < m; i++){
            ans += capacity[i];
            cnt++;
            if(ans >= sum) return cnt;
        }
        return 0;
    }
};

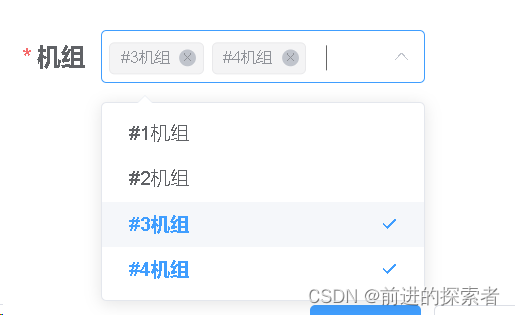
2.幸福值最大化的选择方案（贪心）

思路

降序排序，按顺序依次取孩子

class Solution {
public:
    long long maximumHappinessSum(vector<int>& happiness, int k) {
        int n = happiness.size();
        sort(happiness.begin(), happiness.end(), greater<int>());
        long long sum = 0, x = 0;
        for(int i = 0; i < n && i < k; i++){
            if(happiness[i] - x <= 0) break;
            sum += happiness[i] - x;
            x++;
        }
        return sum;
    }
};

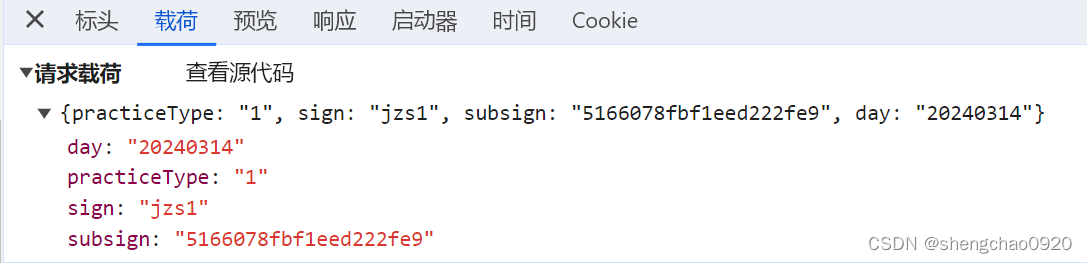
3.数组中的最短非公共子字符串（枚举）

思路

枚举每一种情况

class Solution {
public:
    vector<string> shortestSubstrings(vector<string>& arr) {
        int n = arr.size();
        vector<string> ans;
        // 枚举第几个子串
        for(int k = 0; k < n; k++){
            string ff = "";
            int f = 0;
            // 枚举子串长度
            int m = arr[k].size();
            for(int i = 1; i <= m; i++){
                if(f) break;
                // 枚举子串起始位置
                for(int j = 0; j < m - i + 1; j++){
                    // 判断该子串是否出现过
                    string t = arr[k].substr(j, i);
                    int cnt = 0;
                    for(int z = 0; z < n; z++){
                        string s = arr[z];
                        if(z != k && s.find(t) == -1) cnt++;
                    }
                    if(cnt == n - 1){
                        f = 1;
                        if(t < ff && ff != "") ff = t;
                        else if(ff == "") ff = t;
                    }
                }
            }
            ans.push_back(ff);
        }
        return ans;
    }
};

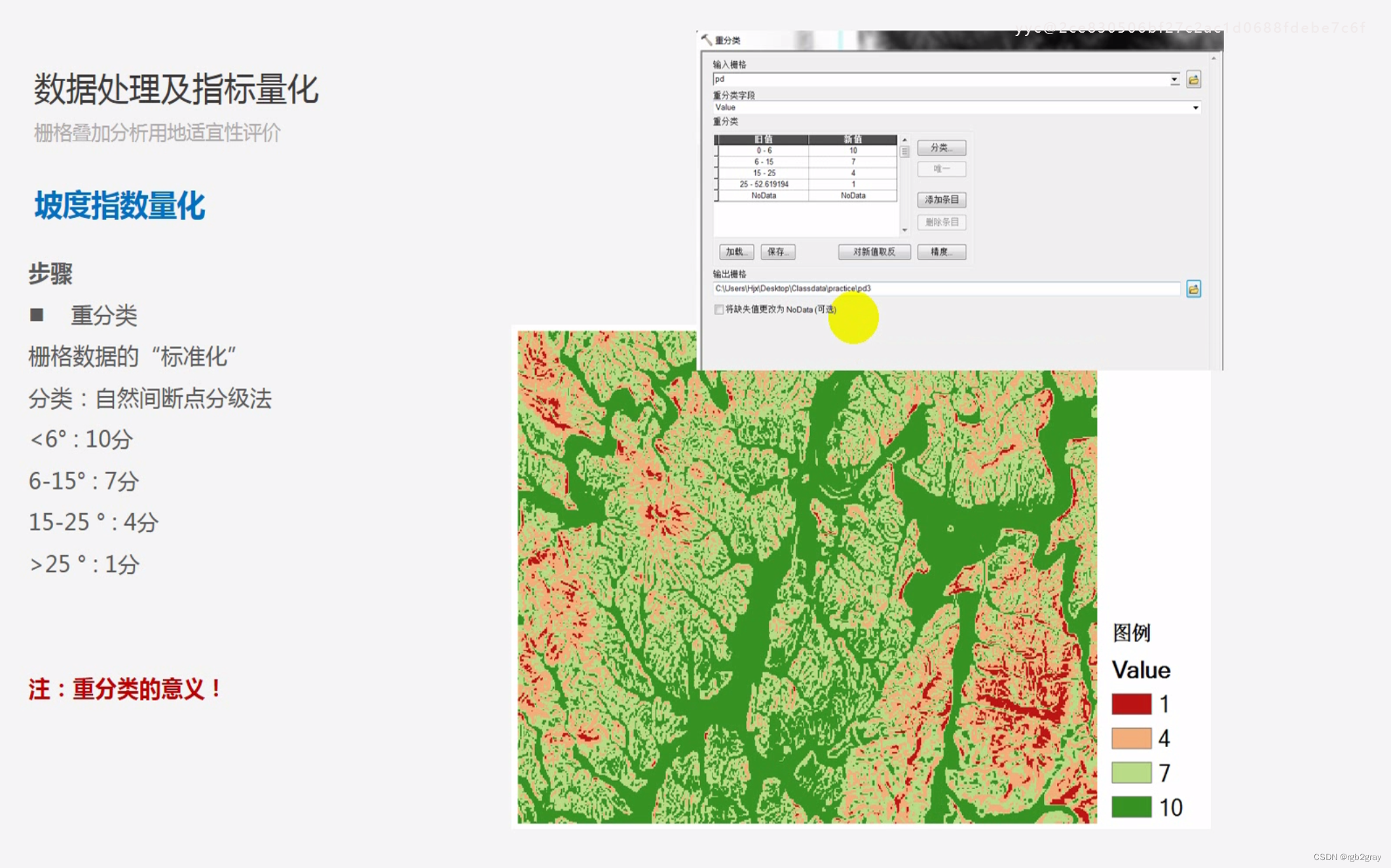
4.K 个不相交子数组的最大能量值（划分 dp）

思路

1.f[i][j]: 从 nums[0] 到 nums[j - 1] 选出 i 个不相交子数组的最大能量值
2.不选 nums[j - 1], f[i][j] = f[i][j - 1]; 选 nums[j - 1], 子数组的元素和为 s[j] - s[L], f[i][j] = f[i - 1][L] + (s[j] - s[L]) * w, (i - 1 <= L <= j - 1)
3.f[0][j] = 0, f[i][i - 1] = 负无穷
4.顺序遍历

class Solution {
public:
    long long maximumStrength(vector<int> &nums, int k) {
        int n = nums.size();
        vector<long long> s(n + 1);
        for(int i = 0; i < n; i++){
            s[i + 1] = s[i] + nums[i];
        }
        vector<vector<long long>> f(k + 1, vector<long long>(n + 1));
        for(int i = 1; i <= k; i++){
            f[i][i - 1] = -1e18;
            long long mx = -1e18;
            int w = (k - i + 1) * (i % 2 ? 1 : -1);
            // j 不能太小也不能太大，要给前面留 i-1 个数，后面留 k-i 个数
            for (int j = i; j <= n - k + i; j++) {
                mx = max(mx, f[i - 1][j - 1] - s[j - 1] * w);
                f[i][j] = max(f[i][j - 1], s[j] * w + mx);
            }
        }
        return f[k][n];
    }
};