目录
- 第一门课:神经网络和深度学习 (Neural Networks and Deep Learning)
- 第二周:神经网络的编程基础 (Basics of Neural Network programming)
- 2.9 逻辑回归中的梯度下降(Logistic Regression Gradient Descent)
第一门课:神经网络和深度学习 (Neural Networks and Deep Learning)
第二周:神经网络的编程基础 (Basics of Neural Network programming)
2.9 逻辑回归中的梯度下降(Logistic Regression Gradient Descent)
本节我们讨论怎样通过计算偏导数来实现逻辑回归的梯度下降算法。它的关键点是几个重要公式,其作用是用来实现逻辑回归中梯度下降算法。但是在本节视频中,我将使用计算图对梯度下降算法进行计算。我必须要承认的是,使用计算图来计算逻辑回归的梯度下降算法有点大材小用了。但是,我认为以这个例子作为开始来讲解,可以使你更好的理解背后的思想。从而在讨论神经网络时,你可以更深刻而全面地理解神经网络。接下来让我们开始学习逻辑回归的梯度下降算法。
假设样本只有两个特征 x 1 x_1 x1和 x 2 x_2 x2,为了计算𝑧,我们需要输入参数 w 1 、 w 2 w_1、w_2 w1、w2 和𝑏,除此之外还有特征值 x 1 x_1 x1和 x 2 x_2 x2。因此𝑧的计算公式为: z = w 1 x 1 + w 2 x 2 + b z = w_1x_1 + w_2x_2 + b z=w1x1+w2x2+b;
回想一下逻辑回归的公式定义如下:
y
^
=
a
=
σ
(
z
)
其中
z
=
w
T
x
+
b
,
σ
(
z
)
=
1
1
+
e
−
z
\hat{y}= a = σ(z) 其中 z= w^Tx + b, σ(z) =\frac{1}{1+e^{-z}}
y^=a=σ(z)其中z=wTx+b,σ(z)=1+e−z1
损失函数:
L
(
y
^
(
i
)
,
y
(
i
)
)
=
−
y
(
i
)
log
(
y
^
(
i
)
)
−
(
1
−
y
(
i
)
)
log
(
1
−
y
^
(
i
)
)
L( \hat{y}^{(i)},y^{(i)}) = -y^{(i)} \log(\hat{y}^{(i)}) - (1-y^{(i)}) \log(1-\hat{y}^{(i)})
L(y^(i),y(i))=−y(i)log(y^(i))−(1−y(i))log(1−y^(i))
代价函数:
J
(
w
,
b
)
=
1
m
∑
i
=
1
m
L
(
y
^
(
i
)
,
y
(
i
)
)
J(w,b) = \frac{1}{m} \sum_{i=1}^{m} L( \hat{y}^{(i)},y^{(i)})
J(w,b)=m1i=1∑mL(y^(i),y(i))
假设现在只考虑单个样本的情况,单个样本的代价函数定义如下:
L
(
a
,
y
)
=
−
(
y
log
(
a
)
+
(
1
−
y
)
log
(
1
−
a
)
)
L( a,y) = -(y \log(a) + (1-y) \log(1-a))
L(a,y)=−(ylog(a)+(1−y)log(1−a))
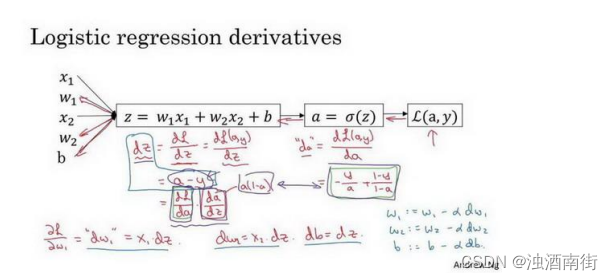
其中𝑎是逻辑回归的输出,𝑦是样本的标签值。现在让我们画出表示这个计算的计算图。
这里先复习下梯度下降法,𝑤和𝑏的修正量可以表达如下:

如图:在这个公式的外侧画上长方形。然后计算: 𝑦^ = 𝑎 = 𝜎(𝑧) 也就是计算图的下一步。最后计算损失函数𝐿(𝑎, 𝑦)。 有了计算图,我就不需要再写出公式了。因此,为了使得逻辑回归中最小化代价函数𝐿(𝑎, 𝑦),我们需要做的仅仅是修改参数𝑤和𝑏的值。前面我们已经讲解了如何在单个训练样本上计算代价函数的前向步骤。现在让我们来讨论通过反向计算出导数。 因为我们想要计算出的代价函数𝐿(𝑎, 𝑦)的导数,首先我们需要反向计算出代价函数𝐿(𝑎, 𝑦)关于𝑎的导数,在编写代码时,你只需要用𝑑𝑎 来表示
d
L
(
a
,
y
)
d
a
\frac{dL(a,y)}{da}
dadL(a,y)。
通过微积分得到: d L ( a , y ) d a = − y a + 1 − y 1 − a \frac{dL(a,y)}{da}=\frac{-y}{a}+\frac{1-y}{1-a} dadL(a,y)=a−y+1−a1−y
如果你不熟悉微积分,也不必太担心,我们会列出本课程涉及的所有求导公式。那么如果你非常熟悉微积分,我们鼓励你主动推导前面介绍的代价函数的求导公式,使用微积分直接求出𝐿(𝑎, 𝑦)关于变量𝑎的导数。如果你不太了解微积分,也不用太担心。现在我们已经计算出𝑑𝑎,也就是最终输出结果的导数。 现在可以再反向一步,在编写 Python 代码时,你只需要用𝑑𝑧来表示代价函数𝐿关于𝑧 的导数
d
L
d
z
\frac{dL}{dz}
dzdL,也可以写成
d
L
(
a
,
y
)
d
z
\frac{dL(a,y)}{dz}
dzdL(a,y),这两种写法都是正确的。
d
L
d
z
=
a
−
y
\frac{dL}{dz} = a-y
dzdL=a−y。
因为
d
L
(
a
,
y
)
d
z
=
d
L
d
z
=
(
d
L
d
a
)
∗
(
d
a
d
z
)
\frac{dL(a,y)}{dz} =\frac{dL}{dz}=(\frac{dL}{da})*(\frac{da}{dz})
dzdL(a,y)=dzdL=(dadL)∗(dzda),并且
d
a
d
z
=
a
∗
(
1
−
a
)
\frac{da}{dz} =a*(1-a)
dzda=a∗(1−a),而
d
L
d
a
=
(
−
y
a
+
1
−
y
1
−
a
)
\frac{dL}{da}= (\frac{-y}{a}+ \frac{1-y}{1-a})
dadL=(a−y+1−a1−y),因此将这两项相乘,得到:
d z = d L ( a , y ) d z = d L d z = d L d a ∗ d a d z = ( − y a + 1 − y 1 − a ) ∗ a ( 1 − a ) = a − y dz=\frac{dL(a,y)}{dz} =\frac{dL}{dz}=\frac{dL}{da}*\frac{da}{dz}=(\frac{-y}{a}+\frac{1-y}{1-a})*a(1-a) =a-y dz=dzdL(a,y)=dzdL=dadL∗dzda=(a−y+1−a1−y)∗a(1−a)=a−y
视频中为了简化推导过程,假设𝑛𝑥这个推导的过程就是我之前提到过的链式法则。如果你对微积分熟悉,放心地去推导整个求导过程,如果不熟悉微积分,你只需要知道𝑑𝑧 = (𝑎 −𝑦)已经计算好了。
现在进行最后一步反向推导,也就是计算𝑤和𝑏变化对代价函数𝐿的影响,特别地,可以用:
d
w
1
=
1
m
∑
n
=
i
m
x
1
(
i
)
(
a
(
i
)
−
y
(
i
)
)
dw_1=\frac{1}{m}\sum_{n=i}^mx_1^{(i)}(a^{(i)} -y^{(i)})
dw1=m1n=i∑mx1(i)(a(i)−y(i))
d
w
2
=
1
m
∑
n
=
i
m
x
2
(
i
)
(
a
(
i
)
−
y
(
i
)
)
dw_2=\frac{1}{m}\sum_{n=i}^mx_2^{(i)}(a^{(i)} -y^{(i)})
dw2=m1n=i∑mx2(i)(a(i)−y(i))
d
b
=
1
m
∑
n
=
i
m
(
a
(
i
)
−
y
(
i
)
)
db=\frac{1}{m}\sum_{n=i}^m(a^{(i)} -y^{(i)})
db=m1n=i∑m(a(i)−y(i))
视频中, 𝑑𝑤1 表示
∂
L
∂
w
1
=
x
1
⋅
d
z
∂L ∂w_1= x_1 ⋅ dz
∂L∂w1=x1⋅dz, 𝑑𝑤2 表示
∂
L
∂
w
2
=
x
2
⋅
d
z
∂L∂w_2= x_2 ⋅ dz
∂L∂w2=x2⋅dz,
d
b
=
d
z
db = dz
db=dz。
因此,关于单个样本的梯度下降算法,你所需要做的就是如下的事情:
使用公式
d
z
=
(
a
−
y
)
dz = (a − y)
dz=(a−y)计算𝑑𝑧,
使用
d
w
1
=
x
1
⋅
d
z
dw_1 = x_1 ⋅ dz
dw1=x1⋅dz 计算𝑑𝑤1,
d
w
2
=
x
2
⋅
d
z
dw_2 = x_2 ⋅ dz
dw2=x2⋅dz计算𝑑𝑤2,
d
b
=
d
z
db= dz
db=dz 来计算𝑑𝑏,
然后: 更新
w
1
=
w
1
−
α
d
w
1
w_1 = w_1 − αdw_1
w1=w1−αdw1, 更新
w
2
=
w
2
−
α
d
w
2
w_2 = w_2 − αdw_2
w2=w2−αdw2, 更新
b
=
b
−
α
d
b
b = b − αdb
b=b−αdb。
这就是关于单个样本实例的梯度下降算法中参数更新一次的步骤。
现在你已经知道了怎样计算导数,并且实现针对单个训练样本的逻辑回归的梯度下降算法。但是,训练逻辑回归模型不仅仅只有一个训练样本,而是有𝑚个训练样本的整个训练集。因此在下一节视频中,我们将这些思想应用到整个训练样本集中,而不仅仅只是单个样本上。