先来看看线性插值的情况

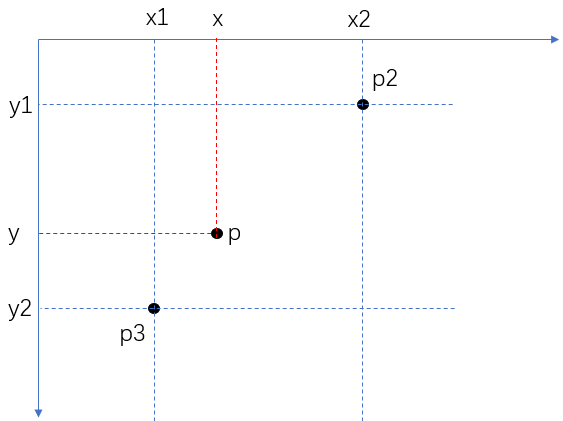
如上图，在已知p2 (x2,y2)和p1 (x1,y1)的情况下要求解在区间[x1,x2]上任意点x对应的y值，有如下公式：

因式分解，解开y有：

可以看出是计算点p与p3的距离权重，是计算点p与p2的距离权重，恰好与他们的坐标相反，在双线性插值中也是如此。

再来看看双线性插值的情况

如上图，还是求解点p的值已知点p的左边(x,y)求f(x,y)，基本思路是现在x方向线性插值求解出f(R1)和f(R2)，再通过f(R1)和f(R2)求解出f(x,y)的值。当然先求解y方向再求解x方向也可以。

求解f(R1)：

求解f(R2):

再在y方向通过f(R1)和f(R2)求解f(x, y):

即通过双线性插值求解了p点的像素值。

一般情况下相邻像素间距为1所以：

如图，令y-y1=v x-x1=u

有：