本篇我们来开始新的话题——决策树
在正式开始讲解之前，我们先来看一个数据集：

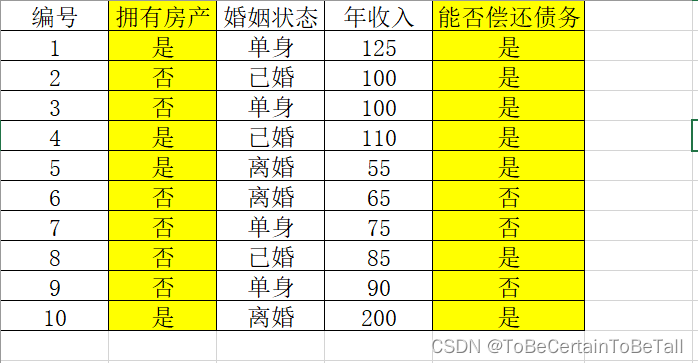
上图展示了银行用于决定是否放贷的数据集。银行通过分析用户特征，预测债务偿还能力，从而决定是否放贷；

针对上面的数据，我们先给出一个决策树的模型：

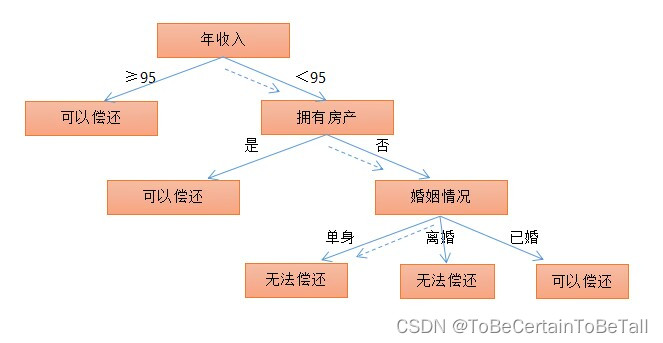
有了这个模型后，当有新数据进入时，我们可以通过数据特征来预测用户是否有能力偿还债务

那么，我们的问题是，怎么构建上图模型？

一. 决策树(Decision Tree)

1. 决策树的构建

对于决策树的构建，我们的主要问题是：

• 首先用哪个特征进行判断呢，即：树的根节点应该是哪个特征？
• 第二层的节点又应该怎样确定呢？

对于节点选择问题，很明显，我们希望最有效（区分度最大）的特征作为根节点，用同样的思路，不断判断区分度最大的特征，从而依次得到下层的节点；如此反复，我们就会得到一个有效的决策树

那么,我们怎样衡量一个划分的“有效性”呢?

1.1 信息熵(Entropy)

1.1.1 信息量&信息熵 定义

• 信息量：如果一个事件发生的概率越大， 那么该事件所蕴含的信息量越少
      比如：“地球的自转与公转” ，因为是确定事件，所以不携带任何信息量
• 信息熵：一个系统越是有序，信息熵就越低；一个系统越是混乱，信息熵就越高
      人话版：信息熵是一个系统的有序程度的度量

信息熵用来描述系统信息量的不确定度

这里我们举一个例子：
A={1，1，1，1，1，1，2，2，2，2}
B={1，2，3，4，5，6，7，8，9，10}

A集合中元素单一化，即信息熵低(越确定，信息熵越低)
B集合中元素多样化，即信息熵高(越不确定，信息熵越高)

1.1.2 高信息熵&低信息熵 定义

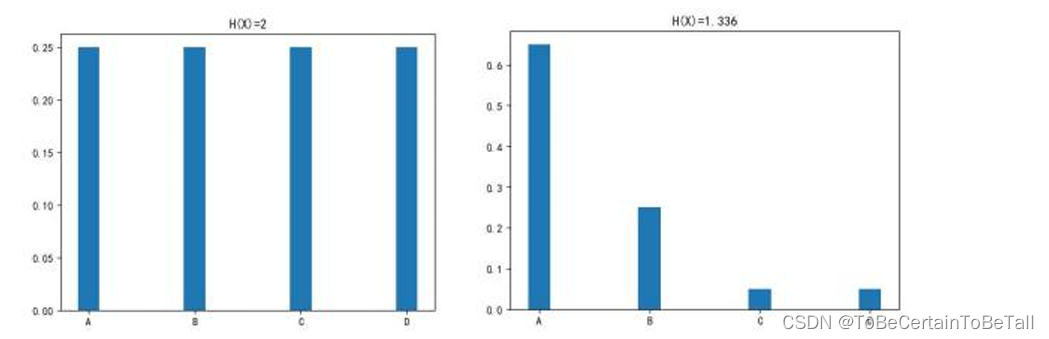
• High Entropy(高信息熵)：随机变量X是均匀分布的，各种取值情况是等概率出现的

• Low Entropy(低信息熵)：随机变量X的各种取值不是等概率出现的

   对于高信息熵与低信息熵，我们讨论的前提是：
   	 1. 都有ABCD四种情况
   	 2. ABCD等概率时，信息熵高 
  

如下图：

左图信息熵高于右图

1.1.3 信息熵 公式

$$H(X)=-\sum _{i=1}^m{p}_i{\log }_2(p_i)$$

公式解释：
参数：
     $p_i$表示第i个元素出现的概率
$H(X)$信息熵的大小：

1. 与m的个数有关
2. 与概率p是否平均有关

解释第一条：m越多，则系统越混乱，熵越大
解释第二条：p越平均，信息熵越大
 

---

例子：
存在一组数据：0.1，0.1，0.1，0.7，0.7，0.7
第一种分法：

（0.1，0.1，0.1）、（0.7，0.7，0.7）

第二种分法：

（0.1，0.1，0.7）、（0.7，0.7，0.1）

最直接的分法为第一种，该分法信息熵为0

1.2 信息增益(Information Gain)

在了解过熵的概念后，我们就可以计算第一次划分得到的信息增益

• 信息增益：用划分之前系统的“熵”减去划分之后系统的“熵”,就是这次划分所获得的“信息增益”

一次划分所获得的“信息增益”越大，则该划分就越有效

1.2.1 信息增益的计算

	简单来说，信息增益就是计算增益的加权和

针对开篇给出的数据集，我们对树的构建方式给出具体计算解释：

系统未划分时：
系统的信息熵(偿还能力值：7是，3否)
$$-\frac{3}{10}{\log }_2\frac{3}{10}-\frac{7}{10}{\log }_2\frac{7}{10}=0.88$$
系统划分时：

1. 按照拥有房产情况划分
   $$-\frac{0}{4}{\log }_2\frac{0}{4}-\frac{4}{4}{\log }_2\frac{4}{4}=0.0$$
   $$-\frac{3}{6}{\log }_2\frac{3}{6}-\frac{3}{6}{\log }_2\frac{3}{6}=1.0$$
   若按照该特征进行划分，信息增益为：
   $$gain=0.88-\frac{4}{10}\ast 0.0-\frac{6}{10}\ast 1.0=0.28$$

2. 按照婚姻状态划分
   $$-\frac{2}{4}{\log }_2\frac{2}{4}-\frac{2}{4}{\log }_2\frac{2}{4}=1.0$$
   $$-\frac{0}{3}{\log }_2\frac{0}{3}-\frac{3}{3}{\log }_2\frac{3}{3}=0.0$$
   $$-\frac{1}{3}{\log }_2\frac{1}{3}-\frac{2}{3}{\log }_2\frac{2}{3}=0.918$$
   若按照该特征进行划分，信息增益为：
   $$gain=0.88-\frac{4}{10}\ast 1.0-\frac{3}{10}\ast 0.0-\frac{3}{10}\ast 0.918=0.21$$

3. 按照年收入划分

针对连续值，我们希望划分可以尽可能的降低系统混乱程度，具体可能出现的分法如下：

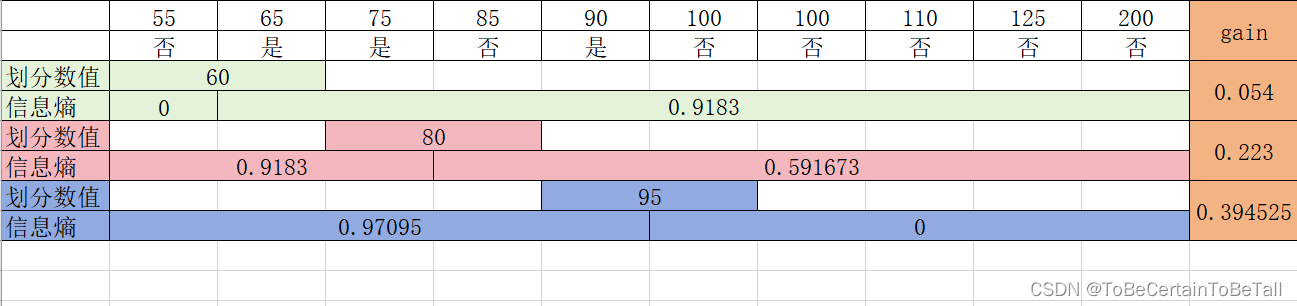
思考：为什么划分数值直接跳过了70？

---

上面，为了得到符合目标的树，我们分别计算了不同特征作为根节点的信息增益，即

$$gain(房产)=0.28$$
$$gain(婚姻)=0.21$$
$$gain(收入)=0.39$$

因此，选择信息增益最大的收入=95作为我们第一次划分划分条件

那么，我们就会得到：

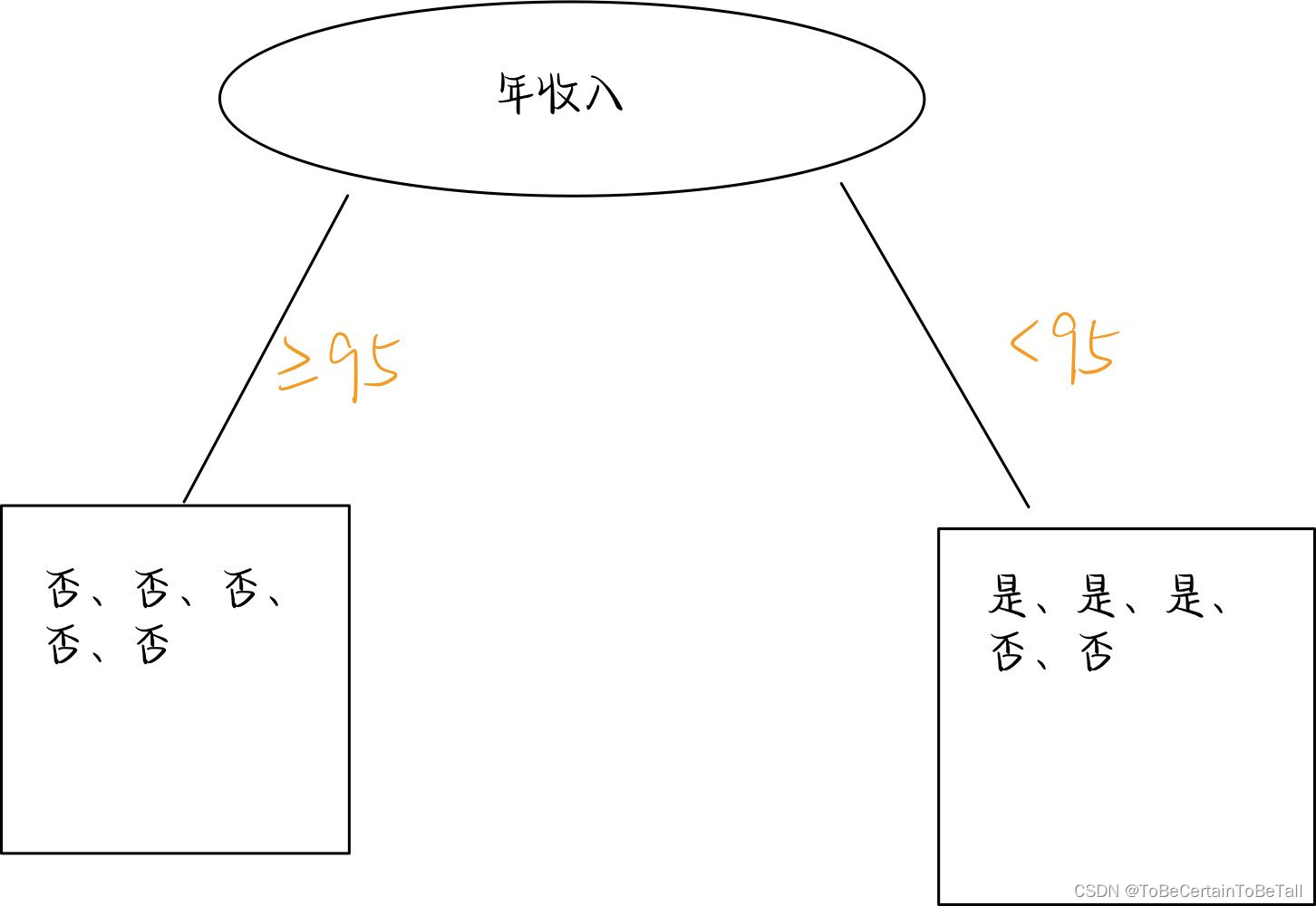
对于第一个节点$\ge 95$信息熵为0，不需要继续划分
对于第二个节点$<95$信息熵大于0，需要继续划分

即，重复上述计算过程，就可以得到一个完整的决策树

1.2.2 小节

样本集合D中含有k类样本，每个类别所占比例分别为$p_k(k=1,2,3,....)$，那么集合D的信息熵为：
$$H(D)=-\sum _{k=1}^k{p}_k{\log }_2{p}_k$$

假设使用离散特征a对集合D进行划分，且特征a有V个取值，那么信息增益为：
$$gain(D,a)=H(D)-\sum _{v=1}^V{p}_k\frac{\left|D_v\right|}{|D|}H(D^v)$$

2. 小节

决策树算法是一种“贪心”算法策略，只考虑当前，未见得是全局最优，不能进行回溯操作(吃葡萄永远只吃最好的)

	决策树是在已知各种情况发生概率的基础上，通过构建决策树来进行分析的一种方式；
		决策树：
			一种树形结构
			每个内部节点表示一个属性的测试
			每个分支表示一个测试输出
			每个叶节点代表一种预测类别
	直观应用概率分析的图解法

2.1 算法分类

决策树是一种常用的有监督算法；从根节点开始，测试待分类项中对应的特征属性，并按照值选择输出分支，直到叶子节点：

1. 将叶子节点存放的类别作为决策结果(分类树)

2. 将叶子节点存放的值作为决策结果(回归树)

    分类树作用：
    	分类标签值
    回归树作用：
    	预测连续值
   

2.2 决策树算法分割选择

根据特征属性的类型不同，在构建决策树的时候，采用不同的方式：

	属性是离散值时，在不要求生成二叉决策树的前提下，一个属性就是一个分支
	属性是离散值时，在要求生成二叉决策树的前提下，分支为“属于此子集”和“不属于此子集”
	属性是连续值时，可以确定一个值作为分裂点，分别按照大于分裂点和小于分裂点生成两个分支

2.3 决策树算法的停止条件

决策树构建是一个递归的过程，如果不给予停止条件，会一直划分，直至叶子节点熵为0；这里我们给出三种常用的停止方式：

	1. 当每个叶子节点只有一种类型时，停止构建；即熵为0 ，节点非常纯(会导致过拟合，一般不用)
	2. 给定树深度值，同时限制叶子节点样本数量小于某个阈值时，停止构建；
	   	   此时对于不纯的节点，采用最大概率类别作为对应类型
	3. 限制分裂前后叶子节点中特征数目 

2.4 决策树算法的评估

对于分类树：

	1. 采用混淆矩阵，即计算准确率，召回率，精确率...
	2. 采用叶子节点的不纯度总和来评估效果，在确定树深和叶子节点个数的前提下，C(T)越小越好

$$C(T)=-\sum _{t=1}^{leaf}\frac{|D^t|}{D}H(t)$$

---

感谢阅读🌼
如果喜欢这篇文章，记得点赞👍和转发🔄哦！
有任何想法或问题，欢迎留言交流💬，我们下次见！

祝愉快🌟！

---