2.1_4 编码和调制

一、第一部分

  比如听收音机的时候，它说，欢迎收听FM109.7。——这个FM就是调制的一种手法。

（一）基带信号与宽带信号

信道

  信号的传输媒介。一般用来表示向某一个方向传送信息的介质，因此一条通信线路往往包含一条发送信道和一条接收信道。

信道上传送的信号

  1.基带信号

  将数字信号1和0直接用两种不同的电压表示，再送到数字信道上去传输（基带传输）。

  来自信源的信号，像计算机输出的代表各种文字或图像文件的数据信号都属于基带信号。基带信号就是发出的直接表达了要传输的信息的信号，比如我们说话的声波就是基带信号。

  2.宽带信号

  将基带信号进行调制后形成的频分复用模拟信号，再传送到模拟信道上去传输（宽带传输）。

  把基带信号经过载波调制后，把信号的频率范围搬移到较高的频段以便在信道中传输（即仅在一段频率范围内能够通过信道）。

  区分“宽带”和“基带”传输，就看好是“数字信道”还是“模拟信道”。

---

  在传输距离较近时，计算机网络采用基带传输方式（近距离衰减小，从而信号内容不易发生变化）。

  在传输距离较远时，计算机网络采用宽带传输方式（远距离衰减大，即使信号变化大也能最后过滤出来基带信号）。

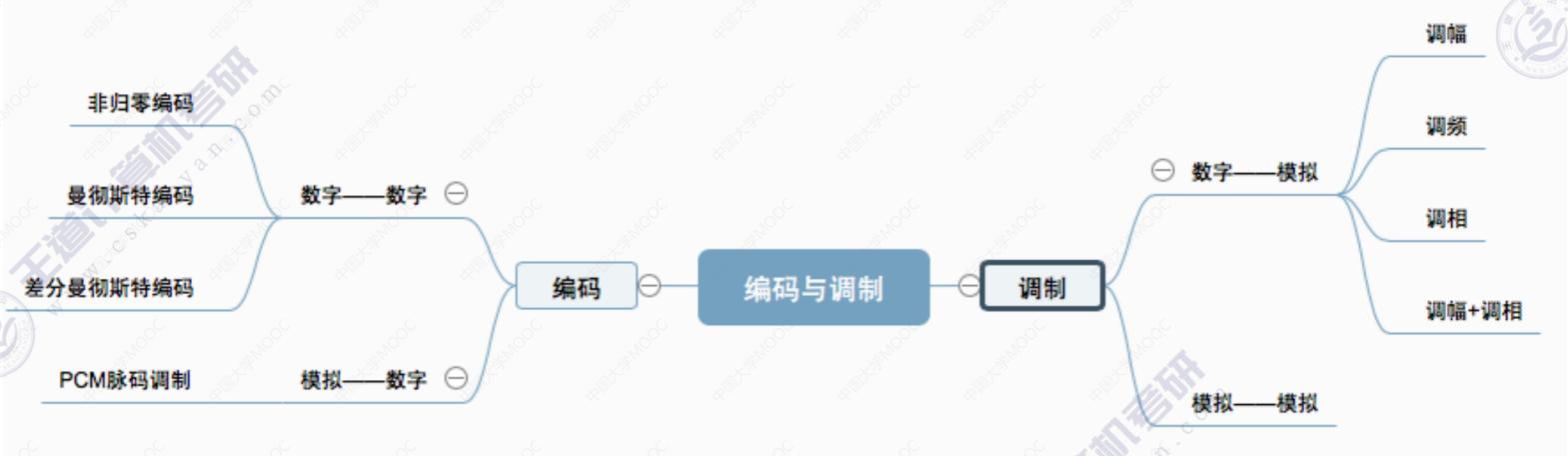
（二）编码与调制

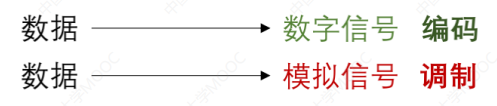
  区分“编码”还是“调制”，就看数据最后转成“数字信号”还是“模拟信号”。

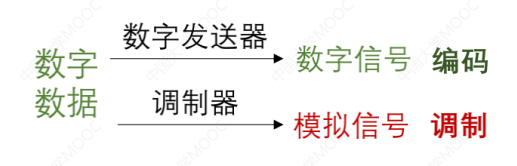
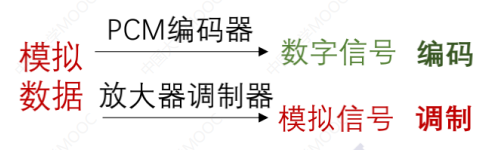
二、第二部分

（一）数字数据编码为数字信号

  “编码”其实就是规定：0和1分别对应什么样的数字信号波形。

  编码方式实际上有很多种，以下给出6种。——其中，前三种是常用的，后三种了解即可。

  1.非归零编码【NRZ】

  2.曼彻斯特编码

  3.差分曼彻斯特编码

  4.归零编码【RZ】

  5.反向不归零编码【NRZI】

  6.4B/5B编码

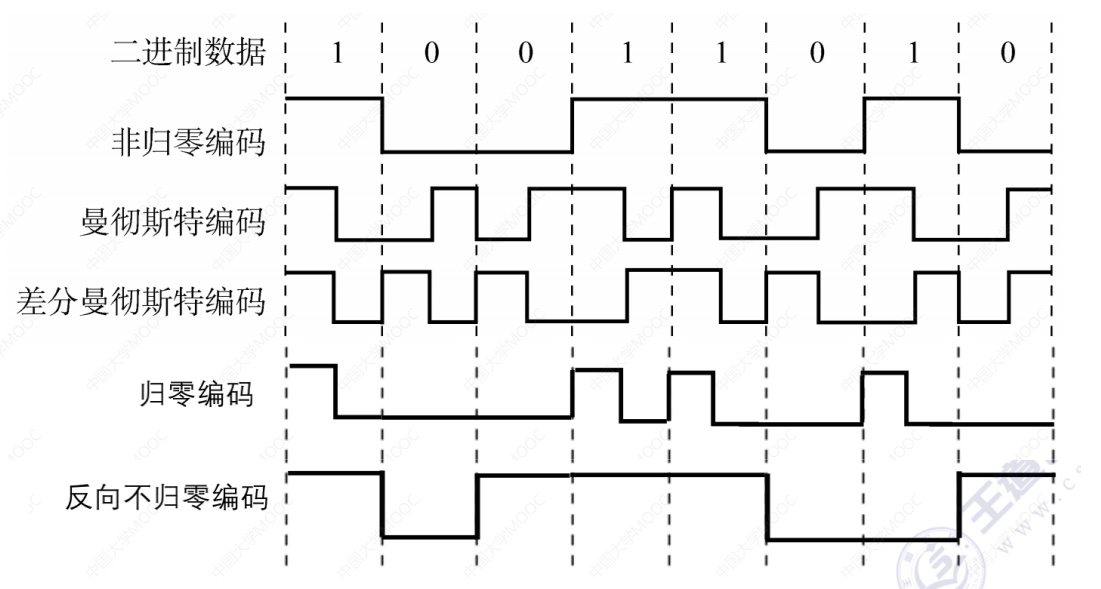
1.非归零编码【NRZ】

  高1低0。

  编码容易实现，但没有检错功能，且无法判断一个码元的开始和结束，以至于收发双方难以保持同步。

  比如，如果发送了连续的1，或连续的0，那么接收端就会收到连续的一条很长的直线，它就不知道是多少个1、多少个0。它就要另外去问发送端，每一个时钟周期是多久？之后才能对这一长条直线进行处理。

  由此，这种编码方式需要发送端、接收端之间再建立一条信道，这个信道就是传输时钟周期的——我要告诉你，多久我会发一个比特，你对应的就是多久接收一个比特。因此还要有一个保持同步的问题。

  但是这种保持同步是比较困难的。因此这种方法不常用。

4.归零编码【RZ】

  信号电平在一个码元之内都要恢复到零的这种编码方式。

  由图可见，对于码元1而言，在一个码元之内，前半段是0，后半段是要归为0的。对于码元0而言，它就保持为0即可。

  对于归零编码，可见，整个传输过程中处于低电平的时候很多、时间很久，所以信道就没怎么用。因此，这种编码也是不推荐使用的。

5.反向不归零编码【NRZI】

  信号电平翻转表示0，信号电平不变表示1。

  “非归零编码”、“反向不归零编码”，它们在一个码元内是不发生跳变的。

  “归零编码”在一个码元内可能发生跳变。

  对于此处的反向不归零编码，如果是“全0”的话，电平就会一直发生反转，同时对于接收端来说它也好接收。但是如果是“全1”，那么接收端还是会不知道，你一共到底发送了多少个1。就又来到了刚才“非归零编码”当中遇到的那个问题。——发送端、接收端要建立一个新的信道，确定好一个时钟周期是多长（每一小段码元是多长）。

  总之，反向不归零编码，对于“全0”的数据还是可以的，但对于“全1”的数据还是会麻烦。

2.曼彻斯特编码

  综合上面那3个编码方式的优缺点，我们就形成了——曼彻斯特编码，这种非常优秀的编码。

  它可以把时钟信号以及数据都放到一块，不需要有额外的信道来传输时钟信号，自己本身就可以实现同步，即自同步。接收端能够直接凭借接收到的数据就能直接判断出所发数据内容是什么，不需要其他的额外操作（如计算时钟周期是多少、提取信号）。

  将一个码元分成两个相等的间隔，前一个间隔为低电平、后一个间隔为高电平表示码元1。码元0则正好相反。也可以采用相反的规定。（具体是哪种规定方式，看题目怎么给出）

  该编码的特点是在每一个码元的中间出现电平跳变，位于中间的跳变既可以作为时钟信号（可用于同步），又作为数据信号。

  所谓的同步，就是发送方发送1个比特，接收方就知道它接收了1个比特；之后发送方再发送第2个比特，接收方也能察觉出这是第2个比特……

  接收方每接收到一个跳变，就对应于1个比特。同时，接收方再看一下这个跳变左右两边的边界值，如果左边高、右边低，说明这1个比特是码元1，码元0同理。

  但它所占的频带宽度是原始的基带宽度的两倍。每一个码元都被调成两个电平，所以数据传输速率只有调制速率的1/2。

  回顾：“码元传输速率”的概念。

  别名码元速率、波形速率、调制速率、符号速率等。它表示单位时间内数字通信系统所传输的码元个数（也可称为脉冲个数或信号变化的次数），单位是波特（Baud）。1波特表示数字通信系统每秒传输一个码元。

  对于“信号变化的次数”的正确理解：如果有两个连续的低电平（即图像是没有波动的，是平的，但是是两个的宽度），此时算作“信号变化”吗？——也算。

  因此，在曼彻斯特编码中，对于每一个码元，在它的中间有一个跳变，即有1个信号变化。但是，在两个码元的交界处，不论是1、0之间的切换，还是1、1或0、0之间的切换，也都算作有1个信号变化。

  因此，对于曼彻斯特编码，它传输1个比特，需要运用2次信号变化。从而，在比特数恒定的情况下，它需要记录2倍的信号变化次数。而码元传输速率表示的也是“单位时间内传输的信号变化的次数”，因此，单位时间内它的数据传输速率就只有调制速率的1/2。

  可以理解为每1个比特需要对应2个码元 / 脉冲个数 / 信号变化的次数。

3.差分曼彻斯特编码

  同1异0。

  这个“同1异0”，看的是两个比特的交界处，即图中“虚线”处。看看虚线的两边是同还是异。

  常用于局域网传输，其规则是：若码元为1，则前半个码元的电平与上一个码元的后半个码元的电平相同。若为0，则相反。

  该编码的特点是，在每个码元的中间，都有一次电平的跳转，可以实现自同步，且抗干扰性强于曼彻斯特编码。

  它抗干扰性为什么较强，是因为它的代码实现逻辑相对较为复杂。

6.4B/5B编码

  比特流中插入额外的比特以打破一连串的0或1，就是用5个比特来编码4个比特的数据，之后再传给接收方，因此称为4B/5B。编码效率为80%。

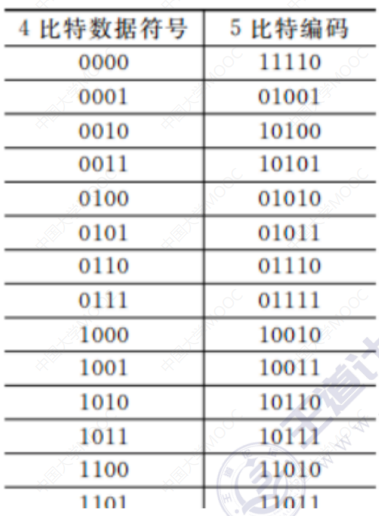
  4比特的编码，总共有16种不同方式。我们对于这16种4比特编码，每个都对应一个5比特编码。5比特位本身是32种编码方式，但只需从中拿出16种去跟4比特编码对应即可。而5比特编码剩下的16种编码，可以用作其他用途，即作为控制码。

  对于5比特编码，只采用16种对应16种不同的4位码，其他的16种作为控制码（帧的开始和结束，线路的状态信息等）或保留。

（二）数字数据调制为模拟信号

  之前在讲“数据通信基础知识”的时候，我们讲过。如果两个主机要通信，而且要通过电话网入网的话，就需要经过模拟信道这样一个过程。

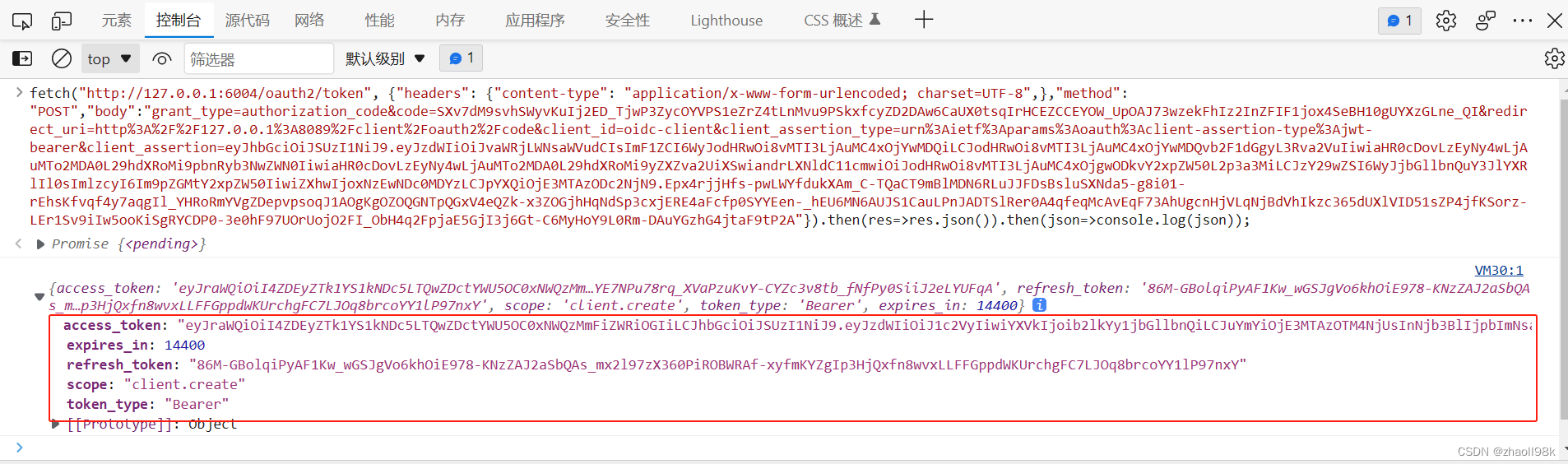
  而由于计算机发出的信号是数字的，所以要放到模拟信道上传输，就需要经过调制解调器，调制成模拟信号，然后才能放到信道上传输。到接收端的时候，再由接收端的调制解调器实现解调过程，把这个模拟信号转成数字信号，进而交给信宿，由信宿把数字信号读出0101是什么样的数据，再把0101转成人们可以识别的图像、文件、音频、视频等等格式。

  数字数据调制技术在发送端将数字信号转换为模拟信号，而在接收端将模拟信号还原为数字信号，分别对应于调制解调器的调制和解调过程。

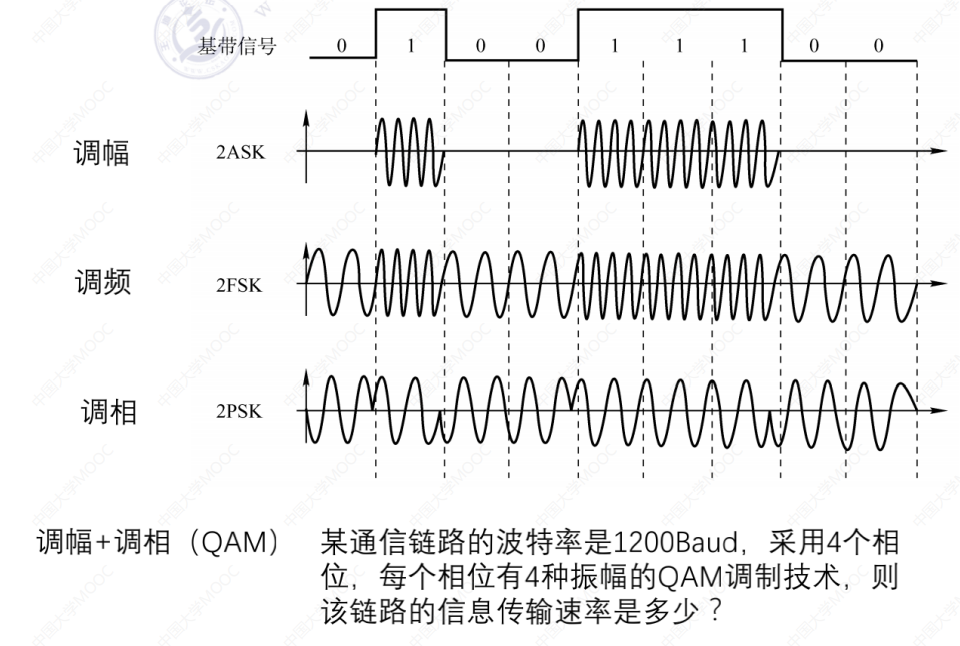
调幅

  如图，0的时候就没有振幅，1的时候就有振幅。就叫调幅。

调频

  如图，0就是低频的，1就是高频的。（低频就是稀疏、比较宽；高频就是比较稠密的）

调相

  调相就是对相位的一种调制。0对应了一种波形，1对应了另一种波形。波形无非也就是正弦波、余弦波。

调幅与调相的结合体——QAM

  在调幅的基础上，对于幅度再进行一个细分，把它调制成几个相位。

  或者说，是在调相的基础之上，对于每一种相位，再给它细分，调成不同的幅度。

  此处常考的就是，把调相、调幅结合在一起的计算问题。

  如题：某通信链路的波特率是1200Baud，采用4个相位，每个相位有4种振幅的QAM调制技术，则该链路的信息传输速率是多少？

  答：采用4个相位，且每个相位有4种振幅，即信号总共有16种不同的波形，即16种码元。

  通过前面的学习可知，16种不同的码元，要采用$lo{g}_{2}16$ = 4进制码元来表示，即要使用四位01比特才能表示16种不同的波形。则每一个码元对应4bit。

  此题给出，该链路的波特率是1200Baud，即每秒钟能够传送1200个码元。问题问的是信息传输速率，也就是比特传输速率，因此是1200 * 4 = 4800 b/s。

（三）模拟数据编码为数字信号

  计算机内部处理的是二进制数据，处理的都是数字音频，所以需要将模拟音频通过采样、量化转换成有限个数字表示的离散序列（即实现音频数字化）。

  最典型的例子就是对音频信号进行编码的脉码调制（PCM），在计算机应用中，能够达到最高保真水平的就是PCM编码，被广泛用于素材保存及音乐欣赏，CD、DVD以及我们常见的WAV文件中均有应用。它主要包括三步：抽样、量化、编码。

1.抽样

  对模拟信号周期性扫描，把时间上连续的信号变成时间上离散的信号。

  为了使所得的离散信号能无失真地代表被抽样的模拟数据，要使用采样定理进行采样：
$$f_{采样频率}\ge 2f_{信号最高频率}$$

  注：这个采样定理的结论先记住，下面再解释。

  之所以要用采样定理进行采样，就是为了保证不同频率的信号都能被采样到。

  此外，对于一种波形，从数学的角度来说，我们取到它上面的两组(x, y)坐标，即可得知它的波形曲线函数。例如，对于正弦波$y=Asin(\omega x+\varphi )$，其中A很好确定，而接下来只需两组(x, y)即可解出两个未知数$\omega$和$\varphi$。

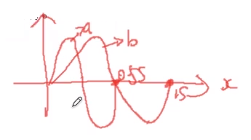
  如图，画了一个“胖”波，记作b波，它的一个周期是1s。还有一个“瘦”波，记作a波，它的一个周期是0.5s。

  频率就是1s振动的次数。因此，b波的频率是：1Hz；a波的频率是：2Hz。我们知道，无论对于a波还是b波，我们只需取得其上两个不同的点坐标，即可解出它的波形图。（采样点不一定是波与x轴的交点，也可能是对应波峰、波谷，也可能是其他位置处）

  接下来考虑采样的频率。如果采样频率是2Hz，即1s内采样两次（即b波频率的二倍）。此时会发生一个问题，我们采样的两个点，不能确定是a波还是b波上的点。例如上图中，如果我们1s内采样两次，采样了(0s, 0)和(0.5s, 0)的话，采样的两个点就不能区分是a波还是b波的点。——因此，按照2Hz的采样频率，就达不到保真的效果。因为，它可能会认为：当前只有b波的存在。或者：它即使知道有a波、b波同时存在，但是无法区分是a还是b。

  如果采样频率是4Hz，即1s内采样四次（即a波频率的二倍）。此外，由于a波是所有波当中最高频的，因此不可能再发生波与波之间区分不开的问题。

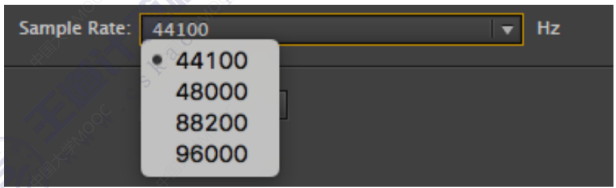
  当然，采样频率可以更高。采样频率越高，我们对于信号波形恢复也就更准确。如下图，我们会在音乐软件中看到这样的东西，采样频率。

2.量化

  把抽样取得的电平幅值按照一定的分级标度转化为对应的数字值，并取整数，这就把连续的电平幅值转换为离散的数字量。

3.编码

  把量化的结果转换为与之对应的二进制编码。

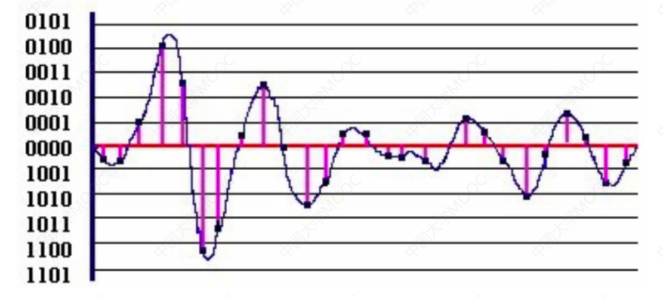
  如图，每隔一个时间段（每个紫色竖线），就对信号采样一次。——抽样

  采样取得的电压，按照一定的分级标度转化为对应的数字值，有正数、负数、整数、小数，全部统一为整数。比如5.2伏，就取5伏。——量化

  经过抽样、量化，我们最终得到它总共有16种状态。总之，我们采用4位二进制编码就足以进行表示了。——编码

（四）模拟数据调制为模拟信号

  在传输过程中，有可能信道非常长、环境很恶劣，就会导致我们要传输的模拟信号受到一定的衰减。

  所以我们就要把模拟信号调制成一个新的模拟信号，以应对传播过程中的干扰。

  为了实现传输的有效性，可能需要较高的频率。这种调制方式还可以使用频分复用技术，充分利用带宽资源。在电话机和本地交换机所传输的信号是采用模拟信号传输模拟数据的方式；模拟的声音数据是加载到模拟的载波信号中传输的。

  如图所示，我通过信号发射塔使用话筒传出模拟信号，由于我的声音是比较低频的，再加上要传播的信道较长、干扰较多，可能我的低频信号传到接收端就已经识别不出了。因此，必须先将我传出的低频信号加强成一个高频的信号。高频的信号就不易受损，且即使受损，也不影响恢复出原来的基带信号。到接收端的时候，再经过解调器，把这个信号解调成基带信号（原来的声波形式），再给收音机来听。

总结